Let f(x)=√|x|−∣x+(where{.} denotes the fractional part of (x)andX,Y are its domain and range, respectively). Then x∈(−∞,12)andY∈(12,∞) x∈(−∞∈,12)∪[0,∞)andY∈(12,∞) X∈(−∞,−12)∪[0,∞)andY∈(12,∞)
x∈(−∞,12] and Y∈[12,∞)
x∈(−∞,−12]∪[0,∞) and Y∈[12,∞)
X∈(−∞,−12]∪[0,∞) and Y∈[0,∞)
None of these
The correct Answer is:C
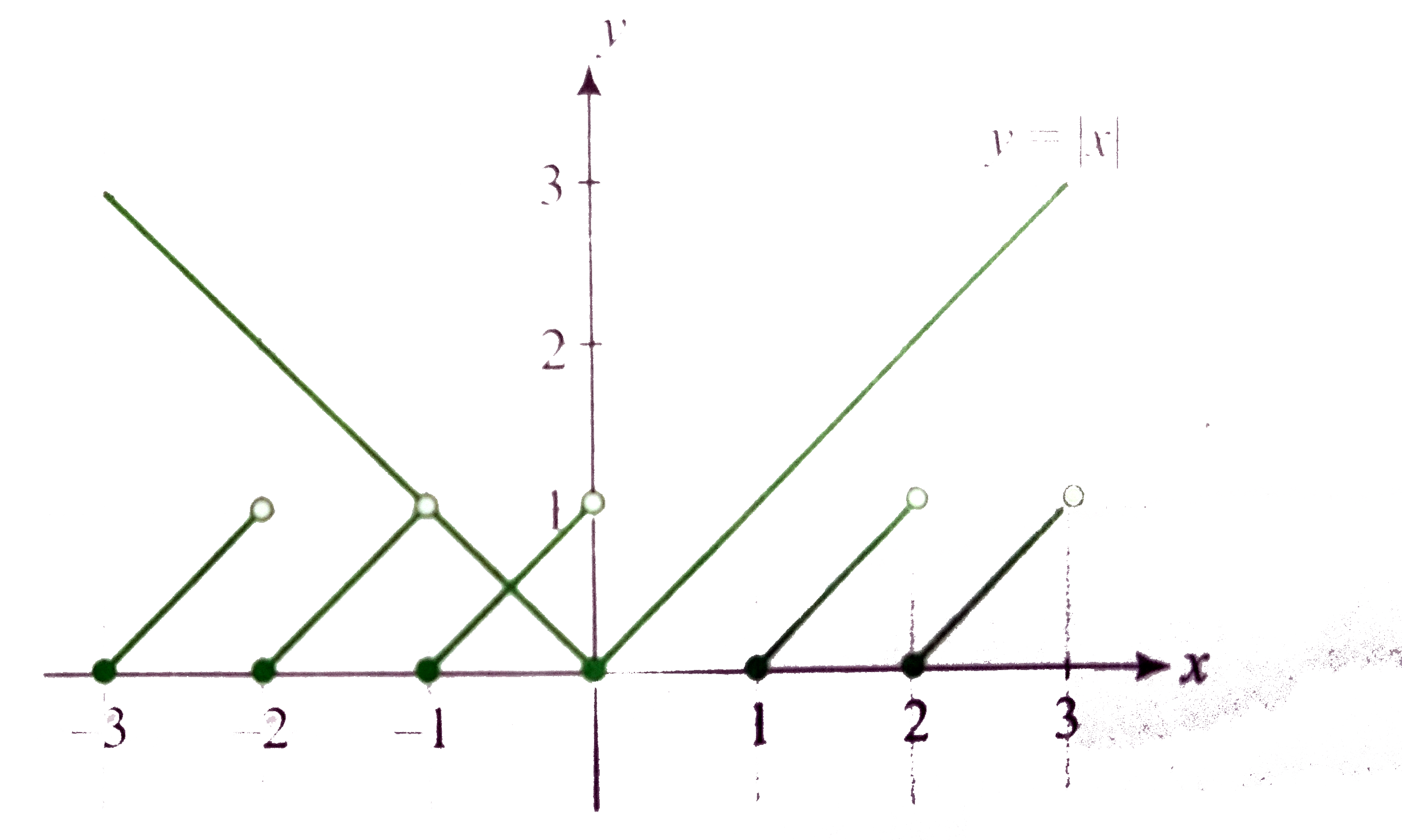
f(x)=√|x|−{x} is defined if |x|≥{x}
or x∈(−∞−12]∪[0,∞) or Y∈[0,∞).
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Multiple Correct Answer Type
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Linked Comprehension Type
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.15
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Let f(x)=√|x|−{x}(where{.} denotes the fractional part of (x)andX,Y are its domain and range, respectively). Then (a) X∈(−∞,12) and Y∈(12,∞) (b)X∈(−∞∈,12)∪[0,∞)andY∈(12,∞) (c)X∈(−∞,−12)∪[0,∞)andY∈[0,∞) (d) none of these
View Solutionlimx→−11√|x|−{−x}(where{x} denotes the fractional part of (x)) is equal to (a)does not exist (b) 1 (c)∞ (d) 12
View SolutionSolution set of the inequation, x2−5x+6x2+x+1<0 is x∈(−∞,2) (b) x∈(2,3) x∈(−∞,2)∪(3,∞) (d) x∈(3,∞)
View SolutionIf |x+2|≤9, then
View SolutionIf |x−1|>5, then a. x∈(−4,6) b. x∈[−4,6] c. x∈(−∞,−4)∪(6,∞) d. x∈(−∞,−4)∪[6,∞)
View SolutionSolution set of the inequation x2+4x+42x2−x−1>0, is x∈(−∞,−2)∪(−2,1) x∈(−∞,−2)∪(−2,−12)∪(1,∞) x∈(−∞,−2)∪(−12,1)∪(1,∞) x∈(−∞,1)
View SolutionIf x and a are real numbers such that a>0 and |x|>a, then (a) x∈(−a,∞) b. x∈[−∞,a) c. x∈(−a,a) d . x∈(−∞,−a)U(a,∞)
View SolutionLet f(x)=[x]cos(π[x+2]) where [ ] denotes the greatest integer function. Then, the domain of f is (a) xεR,x not an integer (b) xε(−∞,−2)∪[−1,∞) (c) xεR,x≠−2 (d) xε(−∞,−1]
View SolutionThe domain of f(x)=log|logx|is (0,∞) (b) (1,∞) (c) (0,1)∪(1,∞) (d) (−∞,1)
View Solutionf(x)=(x−2)|x−3| is monotonically increasing in (a)(−∞,52)∪(3,∞) (b) (52,∞) (c)(2,∞) (d) (−∞,3)
View Solution
