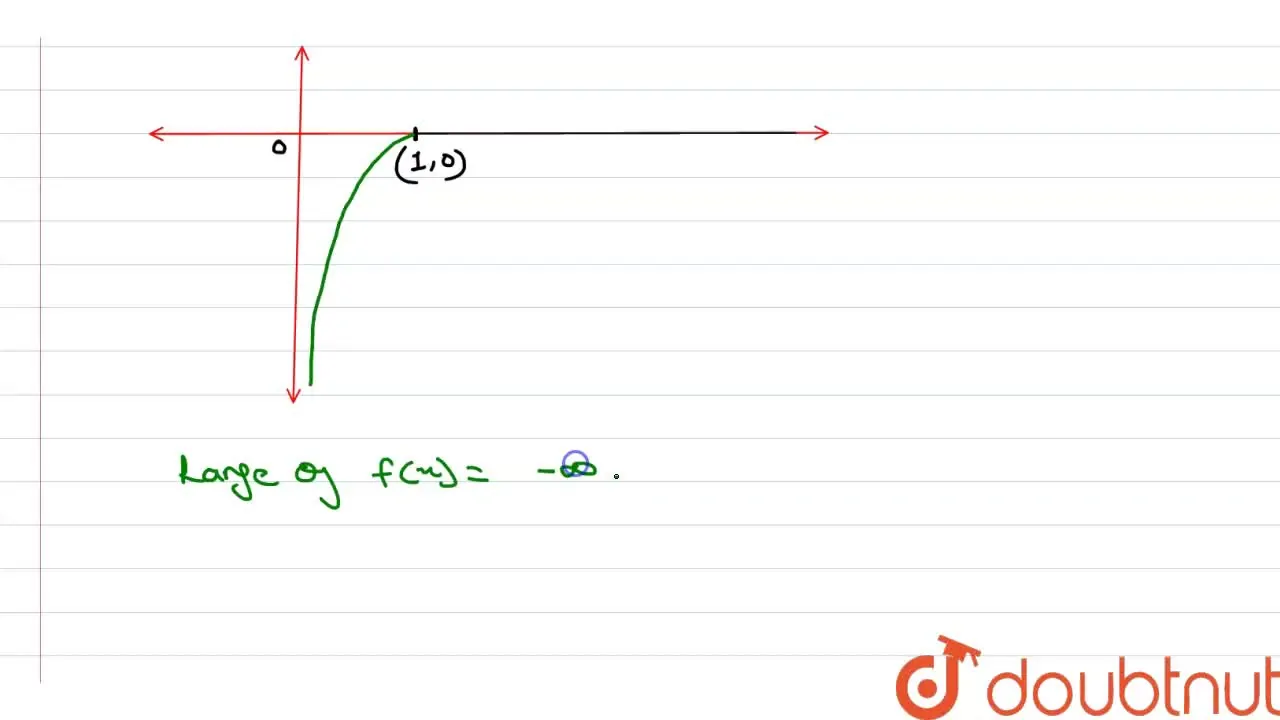
Find the range of f(x)=logex−(logex)2|logex|.
Video Solution
Text Solution
f(x)=logex−(logex)2|logex|
=⎧⎪
⎪⎨⎪
⎪⎩logex−(logex)2(logex),logex>0logex−(logex)2(−logex),logex<0
={0, x>12logex,0<x<1
Therefore, rnge is (−∞,0].
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Solved Examples15videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CONCEPT APPLICATION EXERCISE 1.115videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Find the range of f(x)=(log)ex−((log)ex)2∣∣(log)ex∣∣
View SolutionFind the range of f(x)=cos((log)e{x}).
View SolutionI=∫ loge(logex)x(logex)dx
View SolutionFind the area bounded by y=logex,y=−logex,y=loge(−x),andy=−loge(−x).
View SolutionFind the value of limx→0+3(logex)2+5logex+61+(logex)2.
View SolutionThe differential coefficient of f((log)ex) with respect to x, where f(x)=(log)ex, is
(a)x(log)ex (b) 1x(log)ex (c)1x(log)ex (d) none of theseView SolutionIf f(x)=|logex|,then
View SolutionThe domain of f(x)=log5|logex| , is
View SolutionThe value of
1+(logex)+(logex)22!+(logex)33!+…∞View SolutionFind the range of f(X) =tan−1x−12logex∈(1√3,√3)
View Solution