If sets A=[−4,1]andB=[0,3), then find the following sets:
(a) A∩B (b) A∪B (c ) A−B
(d) B−A (e ) (A∪B)' (f) (A∩B)'
The correct Answer is:(a) [0,1) (b) [−4,3) (c ) [−4,0) (d) [1,3) (e ) (−∞,−4)∪[3,∞) (f) (−∞,0)∪[1,∞)
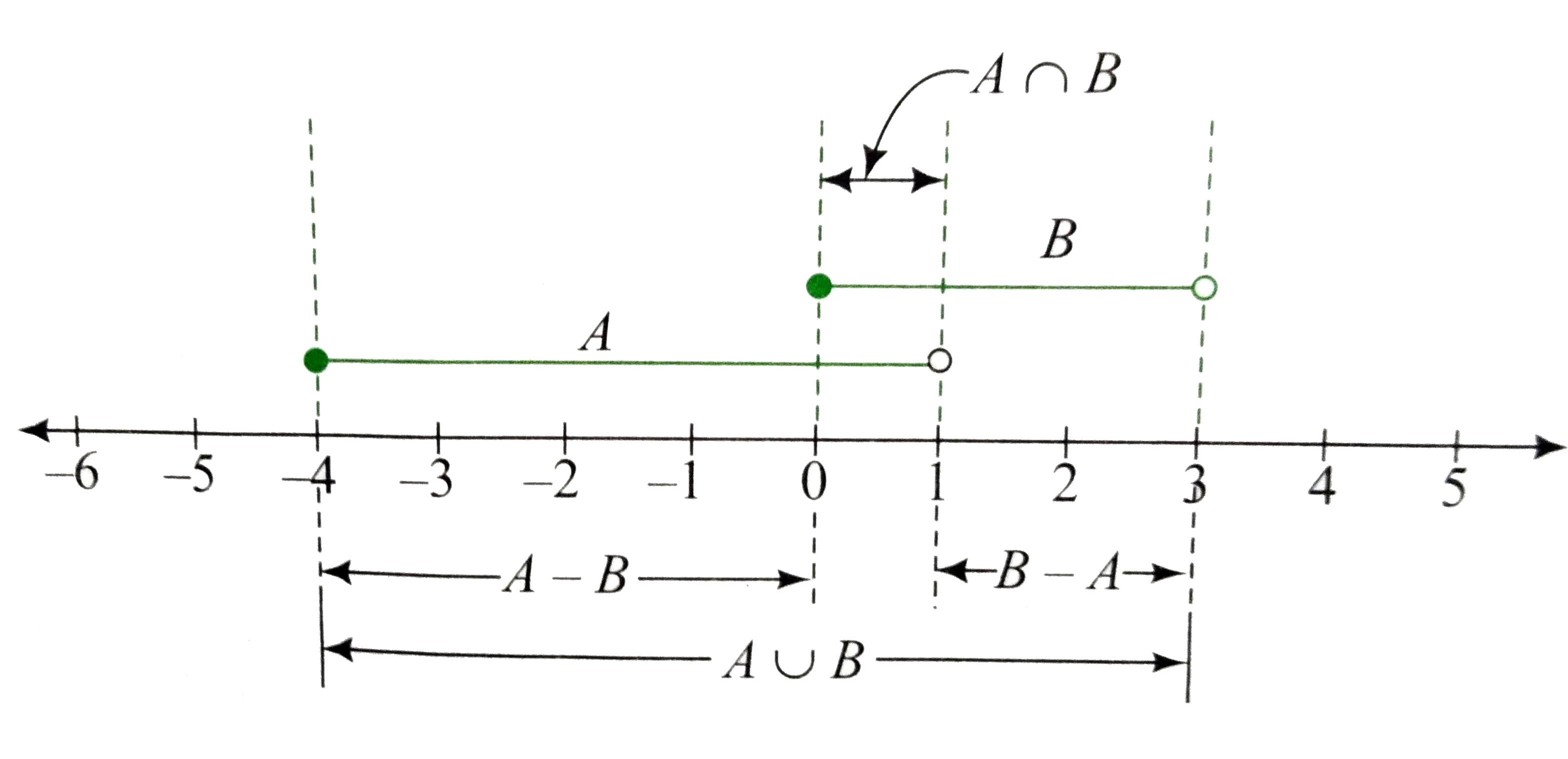
(a) A∩B=[0,1)
(b) A∪B=[−4,3)
(c ) A−B=[−4,0)
(d) B−A=[1,3)
(e ) (A∪B)'=(−∞,−4)∪[3,∞)
(f) (A∩B)'=(−∞,0)∪[1,∞)
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:CONCEPT APPLICATION EXERCISE 1.2
Explore 5 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:CONCEPT APPLICATION EXERCISE 1.3
Explore 9 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Solved Examples
Explore 15 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (Numerical Value Type)
Explore 3 Videos
- SCALER TRIPLE PRODUCTS Book:CENGAGE ENGLISHChapter:SCALER TRIPLE PRODUCTS Exercise:DPP 2.3
Explore 11 Videos
Similar Questions
If A= [-4 , 1 ) and B =[ 0,3), then find A∩B .
View SolutionFor sets (A∪B)∪(A∩B)equals
View SolutionFrom the given diagram find:
(i) A∪B
(ii) A'∩B
(iii) A-B
(iv) B-A
(v) (A∪B)'

View SolutionIf A={1,2,3,4},B={3,4,5},C={1,5,6}, then findof the following :
(i) A∪B
(ii) A∪(B∩C)
(ii) A−B
(iv) A−(B∪C).
View SolutionConsider the following sets:
A= set ofnaturai numbers which are multiples of 2
B= set ofnaturai numbers which are multiples of 3
C= set ofnaturai numbers which are multiples of 5
Then find the following set
(i)A∪B(ii)B∪C(iii)A−B(iv)B−C(v)A∩C<br>(vi)A∩B∩C(vii)(A∪B)−C
View SolutionFrom the adjoining Venn diagram , find the following sets :
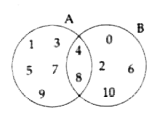
(i) A (ii) B (III) A∪B (iv) A∩B
View SolutionIf A{1,2,3},B={3,4}andC={4,5,6}, then find the each of the following :
(i) A∩(B∪C)
(ii) (A−B)∪C
(iii) (A∪B)−C
(iv) (A∩B)∪C.
View SolutionIf A={1,2,3,4},B={2,4,6,8}andC={3,4,5,6}, then find each of the following ,
(i) (A−B)∩C
(ii) (A∩B)−C
(iii) A−(B−C)
(iv) A∪(B−C).
View SolutionProve A∪(B∩C)=(A∪B)∩(A∪C)
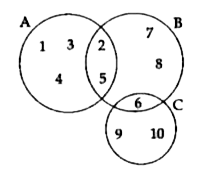
View SolutionFrom the adjoining Venn diagram , write the following sets : (i) A (ii) B (iii) C (iv) A∪B (v) A∩B (vi) B∪C (vii B∩C (viii) A∪C (ix)A∩C
Also verify that :
(i) n(A)+n(B)=(A∪B)+n(A∩B)
(ii) n(B)+n(C)=n(B∪C)+n(B∩C)
View Solution

