A parallelogram containing a 600 angle has perimeter p and its longer diagonal is of length .. Find its area.
To find the area of a parallelogram with a 60∘ angle, given its perimeter P and the length of its longer diagonal D, we can follow these steps:
Step 1: Define the sides of the parallelogram
Let the lengths of the sides of the parallelogram be X and Y. Since the perimeter P is given, we can express it as:
P=2(X+Y)
From this, we can derive:
X+Y=P2(Equation 1)
Step 2: Relate the diagonal D to the sides X and Y
In a parallelogram, the length of the diagonal can be expressed using the cosine of the angle between the sides. For the longer diagonal D and the angle 60∘, we can use the cosine rule:
D2=X2+Y2+2XYcos(60∘)
Since cos(60∘)=12, we can substitute this into the equation:
D2=X2+Y2+XY
Step 3: Rearranging the equation
We can rearrange the equation for D2:
D2=X2+Y2+XY
This can be rewritten as:
D2=(X+Y)2−XY
Substituting X+Y=P2 from Equation 1:
D2=(P2)2−XY
Thus, we can express XY as:
XY=P24−D2(Equation 2)
Step 4: Calculate the area of the parallelogram
The area A of the parallelogram can be calculated using the formula:
A=Base×Height
Here, we can take X as the base and the height as Ysin(60∘). Since sin(60∘)=√32, we have:
A=X⋅Y⋅√32
Substituting XY from Equation 2:
A=(P24−D2)⋅√32
Thus, the area becomes:
A=√32(P24−D2)
Simplifying this gives:
A=√38P2−√32D2
Final Result
The area of the parallelogram is:
A=√38P2−√32D2
Let the lengths of the sides of the parallelogram be X and Y. Since the perimeter P is given, we can express it as:
P=2(X+Y)
From this, we can derive:
X+Y=P2(Equation 1)
In a parallelogram, the length of the diagonal can be expressed using the cosine of the angle between the sides. For the longer diagonal D and the angle 60∘, we can use the cosine rule:
D2=X2+Y2+2XYcos(60∘)
Since cos(60∘)=12, we can substitute this into the equation:
D2=X2+Y2+XY
We can rearrange the equation for D2:
D2=X2+Y2+XY
This can be rewritten as:
D2=(X+Y)2−XY
Substituting X+Y=P2 from Equation 1:
D2=(P2)2−XY
Thus, we can express XY as:
XY=P24−D2(Equation 2)
The area A of the parallelogram can be calculated using the formula:
A=Base×Height
Here, we can take X as the base and the height as Ysin(60∘). Since sin(60∘)=√32, we have:
A=X⋅Y⋅√32
Substituting XY from Equation 2:
A=(P24−D2)⋅√32
Thus, the area becomes:
A=√32(P24−D2)
Simplifying this gives:
A=√38P2−√32D2
The area of the parallelogram is:
A=√38P2−√32D2
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE ENGLISHChapter:TRIGONOMETRIC FUNCTIONS Exercise:Concept Application Exercises 2.1
Explore 8 Videos
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE ENGLISHChapter:TRIGONOMETRIC FUNCTIONS Exercise:Concept Application Exercises 2.2
Explore 8 Videos
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE ENGLISHChapter:TRIGONOMETRIC FUNCTIONS Exercise:SINGLE CORRECT ANSWER TYPE
Explore 38 Videos
- TRIGONOMETRIC EQUATIONSBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC EQUATIONSExercise:Archives (Matrix Match Type)
Explore 1 Video
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASExercise:Matrix Match Type
Explore 1 Video
Similar Questions
A parallelogram containing a 600 angle has perimeter p and its longer diagonal is of length d Find its area.
View SolutionThe perimeter of a rhombus is 52 cm. If one diagonal is 24 cm, find :
its area.
View SolutionThe perimeter of a rectangular plot is 52m and its length is 17m. Find its
area.
View SolutionA rectangle has perimeter 132 cm. Its length is 9 cm more than twice its breadth . Find its area.
View SolutionThe perimeter of a square is numerically equal to its area. Find its area.
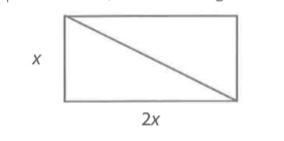
View SolutionIf the rectangle shown has a perimeter of 6, what is its diagonal?
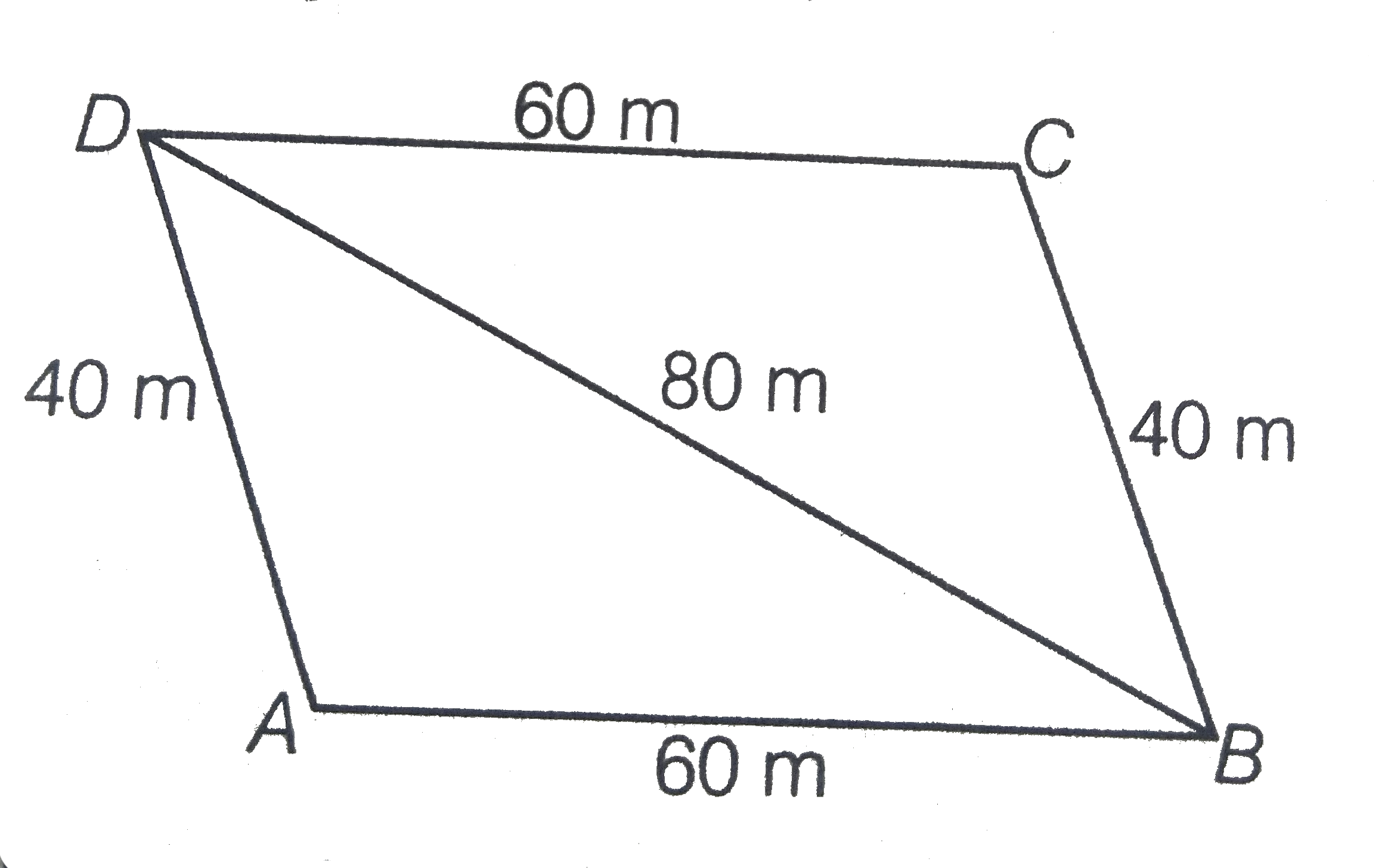
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View SolutionFind the dimensions of a rectangle with perimeter 72 units and whose length is five times its breadth. Also, find its area.
View SolutionTwo adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
View SolutionThe area of a rhombus is 216 sq. cm. If its one diagonal is 24 cm, find :
length of its side,
View Solution

