A parallelogram containing a 600 angle has perimeter p and its longer diagonal is of length d Find its area.
To find the area of a parallelogram that contains a 60∘ angle, has a perimeter p, and a longer diagonal of length d, we can follow these steps:
Step 1: Define the sides of the parallelogram
Let the lengths of the sides of the parallelogram be x and y. Since it is a parallelogram, the opposite sides are equal, so we have:
- Side 1 = x
- Side 2 = y
Step 2: Use the perimeter to find a relationship between x and y
The perimeter p of the parallelogram can be expressed as:
p=2(x+y)
From this, we can derive:
x+y=p2(Equation 1)
Step 3: Analyze the diagonal using the cosine rule
The longer diagonal d can be calculated using the cosine rule in triangle ABE (where E is the intersection of the diagonals):
d2=x2+y2−2xycos(60∘)
Since cos(60∘)=12, we can substitute this into the equation:
d2=x2+y2−xy
Step 4: Substitute y in terms of x using Equation 1
From Equation 1, we can express y as:
y=p2−x
Now substitute y into the diagonal equation:
d2=x2+(p2−x)2−x(p2−x)
Step 5: Simplify the expression for d2
Expanding the terms:
d2=x2+(p24−px+x2)−(px2−x2)
Combining like terms:
d2=2x2−px2+p24
Step 6: Rearranging to find xy
Rearranging gives us:
xy=p24−d2
Step 7: Calculate the area of the parallelogram
The area A of the parallelogram can be calculated using the formula:
A=base×height
Here, we can take x as the base and the height corresponding to angle 60∘ is given by ysin(60∘):
A=x⋅(ysin(60∘))=xy⋅√32
Substituting xy from the previous step:
A=(p24−d2)⋅√32
Thus, the area can be expressed as:
A=√32(p24−d2)
Final Area Expression
Simplifying gives:
A=√38p2−√32d2
Let the lengths of the sides of the parallelogram be x and y. Since it is a parallelogram, the opposite sides are equal, so we have:
- Side 1 = x
- Side 2 = y
The perimeter p of the parallelogram can be expressed as:
p=2(x+y)
From this, we can derive:
x+y=p2(Equation 1)
The longer diagonal d can be calculated using the cosine rule in triangle ABE (where E is the intersection of the diagonals):
d2=x2+y2−2xycos(60∘)
Since cos(60∘)=12, we can substitute this into the equation:
d2=x2+y2−xy
From Equation 1, we can express y as:
y=p2−x
Now substitute y into the diagonal equation:
d2=x2+(p2−x)2−x(p2−x)
Expanding the terms:
d2=x2+(p24−px+x2)−(px2−x2)
Combining like terms:
d2=2x2−px2+p24
Rearranging gives us:
xy=p24−d2
The area A of the parallelogram can be calculated using the formula:
A=base×height
Here, we can take x as the base and the height corresponding to angle 60∘ is given by ysin(60∘):
A=x⋅(ysin(60∘))=xy⋅√32
Substituting xy from the previous step:
A=(p24−d2)⋅√32
Thus, the area can be expressed as:
A=√32(p24−d2)
Simplifying gives:
A=√38p2−√32d2
Topper's Solved these Questions
Similar Questions
A parallelogram containing a 600 angle has perimeter p and its longer diagonal is of length .. Find its area.
View SolutionThe perimeter of a rhombus is 52 cm. If one diagonal is 24 cm, find :
its area.
View SolutionThe perimeter of a square is numerically equal to its area. Find its area.
View SolutionThe perimeter of a rectangular plot is 52m and its length is 17m. Find its
area.
View SolutionA rectangle has perimeter 132 cm. Its length is 9 cm more than twice its breadth . Find its area.
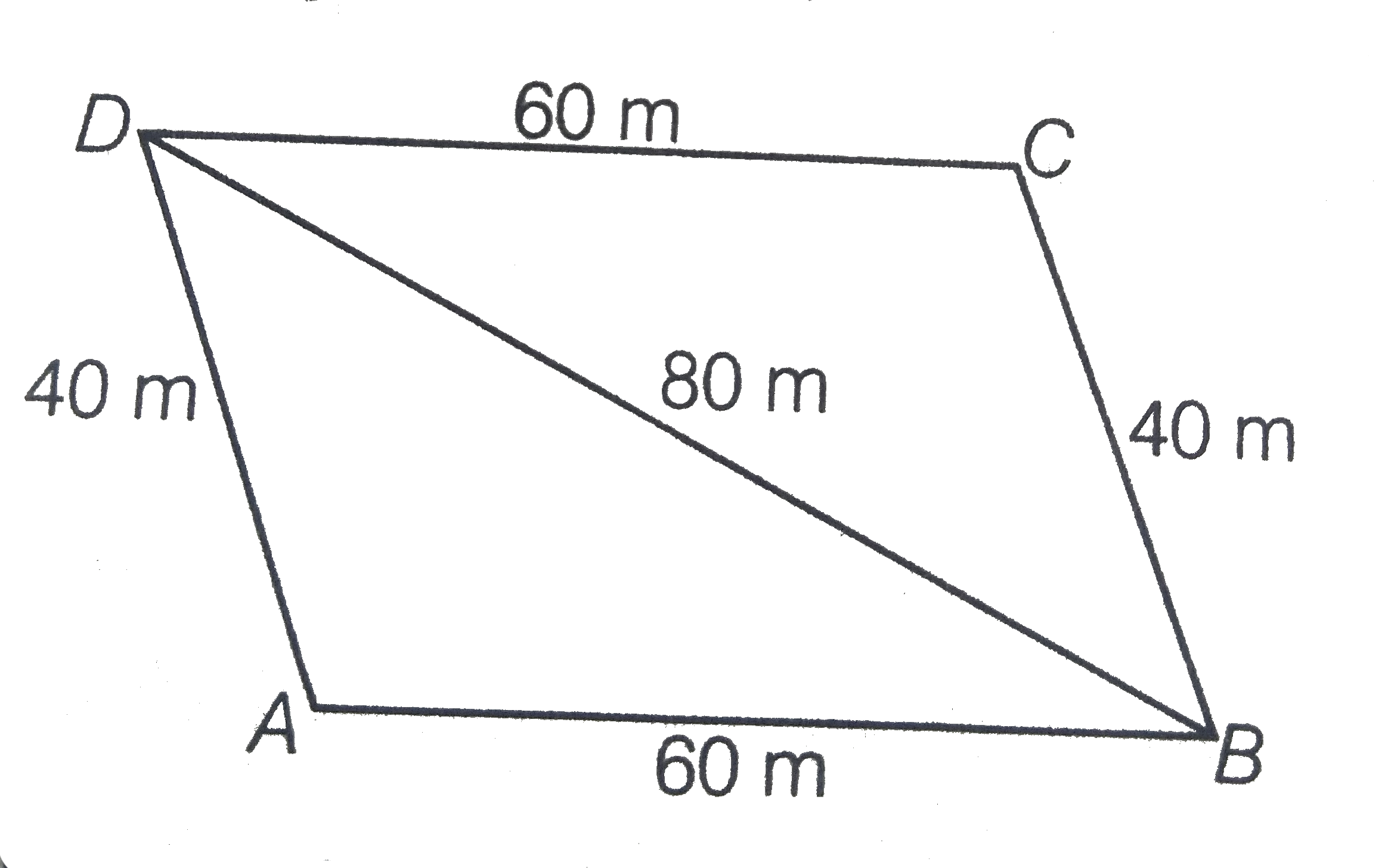
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
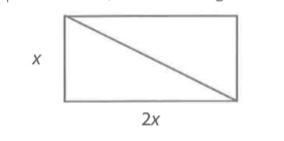
View SolutionIf the rectangle shown has a perimeter of 6, what is its diagonal?
View SolutionTwo adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
View SolutionThe area of a rhombus is 216 sq. cm. If its one diagonal is 24 cm, find :
length of its side,
View SolutionThe perimeter of a square is 48 cm. Find its area.
View Solution
