Find the value of x for which f(x)=√sinx−cosx is defined, x∈[0,2π).
f(x)=√sinx−cosx is defined if sinx≥cosx.
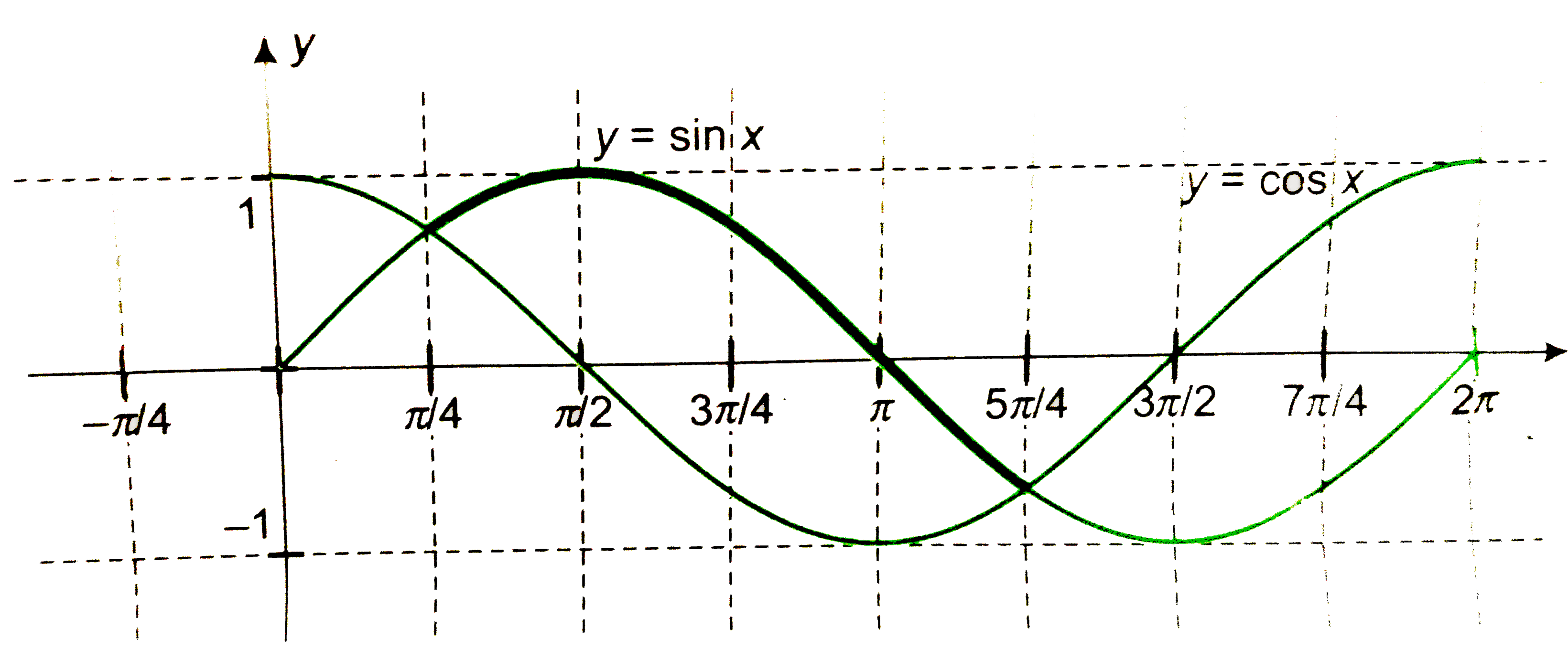
From the graph, sinx≥cosx,forx∈[π4,5π4].
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - example
10 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.1
8 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Video
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Video
Similar Questions
Find the value of x in [−π,π] for which f(x)=√(log)2(4sin2x−2√3sinx−2sinx+√3+1) is defined.
View SolutionFind the value of a in order that f(x)=√3sinx−cosx−2ax+b decreases for all real values of x.
View SolutionFind the value of a in order that f(x)=√3sinx−cosx−2ax+b decreases for all real values of x.
View SolutionFind the value of a for which the function f defined by f(x)={asin(π2)(x+1),x≤0tanx−sinxx3,x>0 is continuous,at x=0
View SolutionFind the intervals in which f(x)=sinx−cosx , where 0<x<2π is increasing or decreasing.
View SolutionWrite the interval in which f(x)=sinx+cosx, x∈[0, π/2] is increasing.
View SolutionThe maximum value of f(x)=sin2xsinx+cosx in the interval (0,π2) is
View SolutionFind all the points of local maxima and minima of the function f given by f(x)=sinx−cosx,x∈[0,2π]
View SolutionFind the intervals in which the function f given by f(x)=4sinx−2x−xcosx2+cosxis increasing decreasing, x∈(0,2π)
View SolutionFind the maximum and minimum values of f(x)=sinx+12cos2x in [0, π2] .
View Solution