A circle is inscribed in an equilateral triangle of side a. Find the area of any square inscribed in this circle.

Video Solution

Text Solution

Verified by Experts

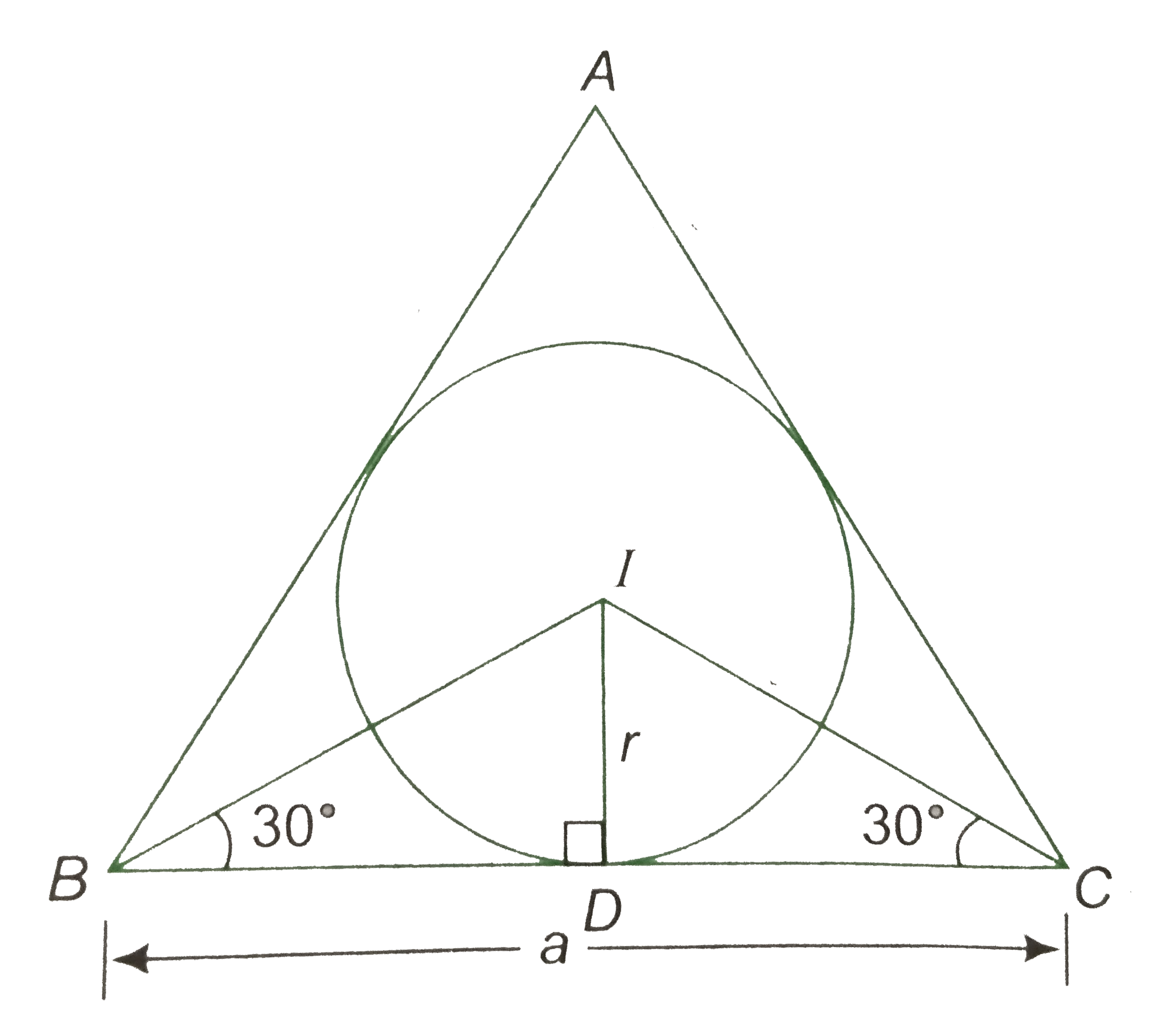
In the above figure, circle with centre I is inscribed in an equilateral triangle ABC.
BC and BA are two tangents from B to circle, therefore must be the angle bisector of $∠ B$ .
But $∠ B = 60^{\circ} (∴ Δ A B C is an equilateral Δ)$
$∴ ∠ I B D = 30^{\circ}$
$∴ {tan 30}^{\circ} = \frac{r}{a / 2}$
$∴ r = \frac{a}{2 \sqrt{3}}$
Now, inside the circle, square PQRS is inscribad.

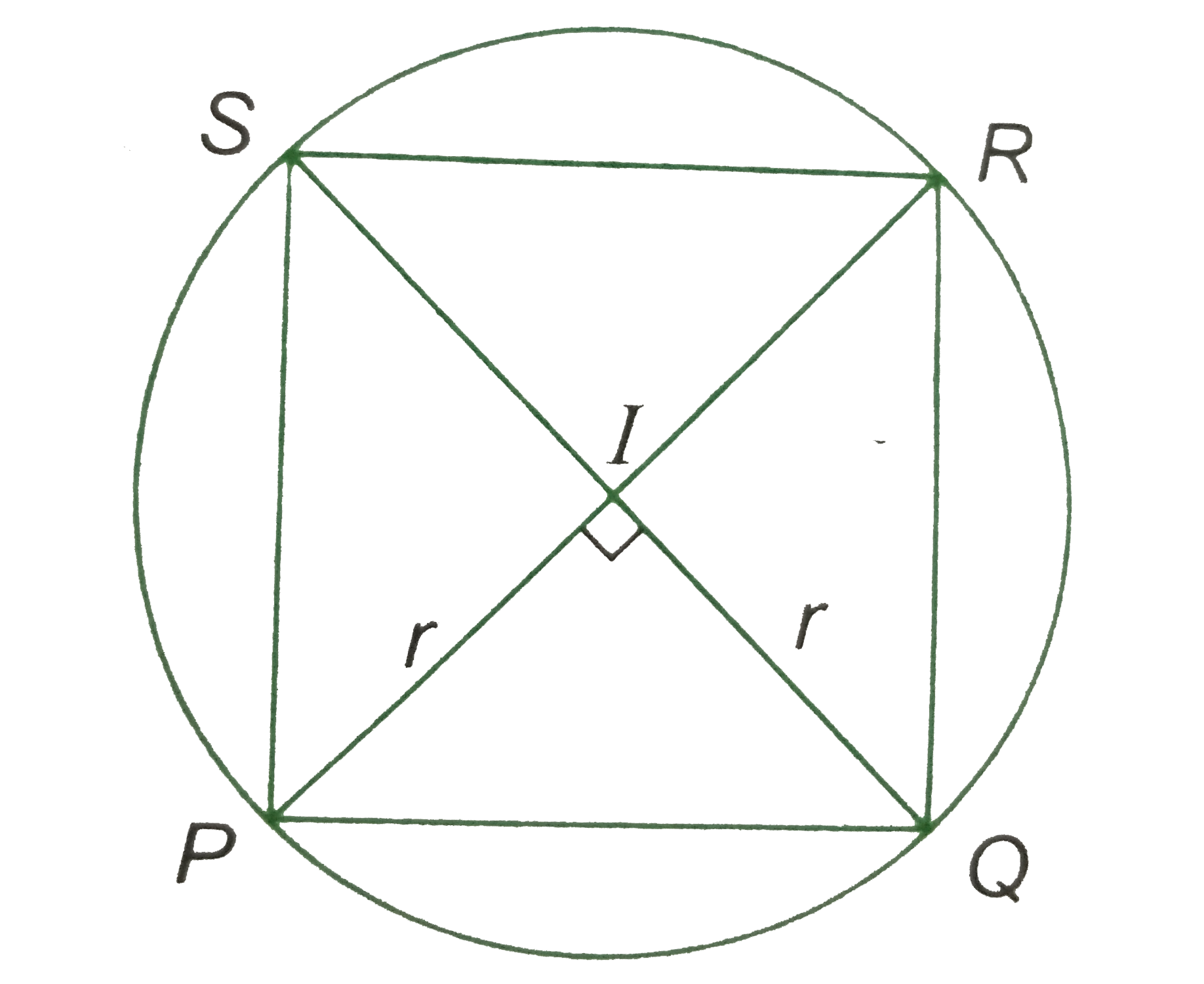
In the above figure, IPQ is isosceles-right angled triangle.
$∴ P Q^{2 = I P^{2} + I Q^{2} = r^{2} + r^{2} = 2 r^{2}}$
$\Rightarrow P Q = \sqrt{2} \times \frac{a}{2 \sqrt{3} = \frac{a}{\sqrt{6}}}$
$∴ Area of square = {(\frac{a}{\sqrt{6}})}^{2} = \frac{a^{2}}{6} sq. unit$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE

Home
Ask Doubt
Profile