The postion vectors of the vertices of a quadrilateral with A as origin are . Prove that the area of the quadrilateral is .
Area of quandrilateral is
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Exercise 2.1
Explore 18 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Exercise 2.2
Explore 15 Videos
- DETERMINANTSBook:CENGAGE ENGLISHChapter:DETERMINANTSExercise:All Questions
Explore 264 Videos
- DIFFERENTIAL EQUATIONSBook:CENGAGE ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:Matrix Match Type
Explore 5 Videos
Similar Questions
The postion vectors of the vertrices fo aquadrilateral with A as origian are B(→b),D(→d)andC(l→b+m→d) . Prove that the area of the quadrilateral is 12(l+m)∣∣→b×→d∣∣.
View SolutionThe position vectors of the vertices of a quadrilateral with A as origin are B(→b),D(→d)andC(l→b+m→d). Prove that the area of the quadrialateral is 12(l+m)∣∣→b×→d∣∣.
View Solution
Knowledge Check
If →A×→B=→C+→D, them select the correct alternative:
A→B is parallel to →C+→D.B→A is perpendicular to →C.CComponent of →C along →A = component of →D along →ADComponent of →C along →A= - component of →D along →A
The position vectors of the vertices A, B and C of a triangle are three unit vectors →a,→band→c respectively. A vector →d is such that →d.ˆa=→d.ˆb=→d.ˆcand→d=λ(ˆb+ˆc) . Then triangle ABC is
View SolutionThe position vectors of the vertices A, B and C of a triangle are three unit vectors →a,→band→c respectively. A vector →d is such that →d.ˆa=→d.Hatb=→d.ˆcand→d=λ(ˆb+ˆc) . Then triangle ABC is
View SolutionIf →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
View SolutionIf →a,→b,→c,→d are the position vectors of the verticles of a cyclic quadrilateral ABCd prove that
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=0
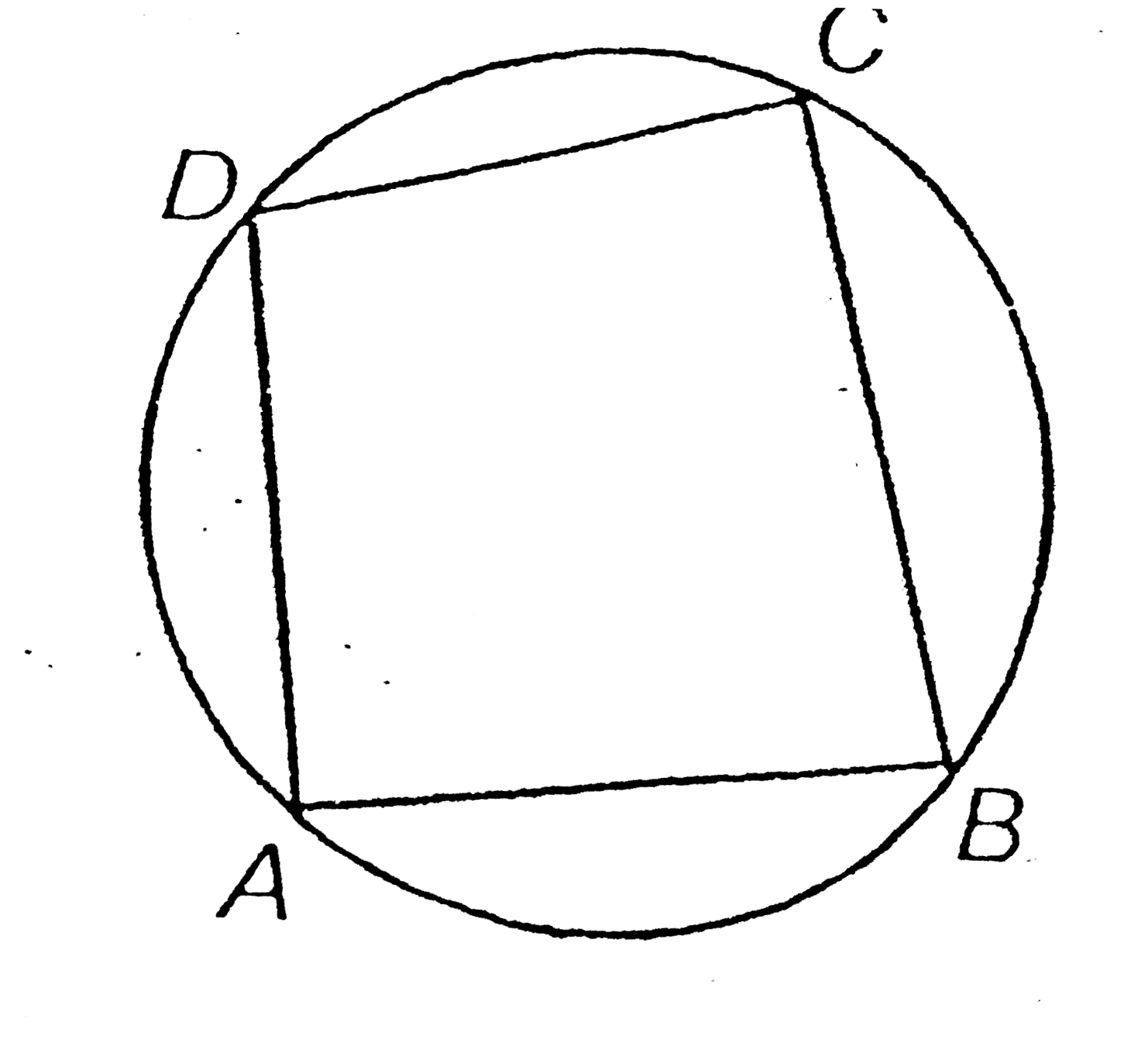
View SolutionGiven →C=→A×→Band→D=→B×→A. What is the angle between →C and →D ?
View SolutionProve that the perpendiculasr distanceof as point with position vector →a from the plane thorugh three points with position vectors →b,→c,→d is [→a→c→d]+[→a→d→b]+[→a→b→c]−[→b→c→d]∣∣∣→b×→c+→c×→d+−→dx→b∣∣∣
View SolutionLet the pair of vector →a,→b and →c,→d each determine a plane. Then the planes are parallel if
View Solution