The maximum area of the convex polyon formed by joining the points A(0,0),B(2t2,0),C(18,2),D(8r2,4) and E(0,2) where t∈R−{0} and interior angle at vertex B is greater than or equal to 90∘ is
The correct Answer is:54
To find the maximum area of the convex polygon formed by the points A(0,0),B(2t2,0),C(18,2),D(8r2,4),E(0,2) with the condition that the interior angle at vertex B is greater than or equal to 90∘, we can follow these steps:
Step 1: Identify the points and their coordinates
We have the following points:
- A(0,0)
- B(2t2,0)
- C(18,2)
- D(8r2,4)
- E(0,2)
Step 2: Determine the area of the polygon
The area of a polygon can be calculated using the formula:
Area=12|x1y2+x2y3+x3y4+x4y5+x5y1−(y1x2+y2x3+y3x4+y4x5+y5x1)|
Substituting the coordinates of points A,B,C,D,E:
- (x1,y1)=(0,0)
- (x2,y2)=(2t2,0)
- (x3,y3)=(18,2)
- (x4,y4)=(8r2,4)
- (x5,y5)=(0,2)
Step 3: Calculate the area using the coordinates
Substituting into the area formula:
Area=12∣∣∣0⋅0+2t2⋅2+18⋅4+8r2⋅2+0⋅0−(0⋅2t2+0⋅18+2⋅8r2+4⋅0+2⋅0)∣∣∣
This simplifies to:
Area=12∣∣∣0+4t2+72+16r2+0−(0+0+16r2+0+0)∣∣∣
=12∣∣4t2+72∣∣
=2t2+36
Step 4: Maximize the area under the given conditions
To maximize the area 2t2+36, we can observe that as t increases, the area increases. However, we need to ensure that the angle at B is ≥90∘.
Step 5: Condition for angle at B
The angle at B will be ≥90∘ if the slopes of lines AB and BC satisfy:
slope of AB⋅slope of BC≤−1
Calculating the slopes:
- Slope of AB=0−02t2−0=0
- Slope of BC=2−018−2t2=218−2t2
Since the slope of AB is 0, we need to ensure that 218−2t2 is undefined or negative, which occurs when 18−2t2≤0 or t2≥9.
Step 6: Find the maximum area
Substituting t2=9 into the area formula:
Area=2(9)+36=18+36=54
Thus, the maximum area of the convex polygon is 54.
We have the following points:
- A(0,0)
- B(2t2,0)
- C(18,2)
- D(8r2,4)
- E(0,2)
The area of a polygon can be calculated using the formula:
Area=12|x1y2+x2y3+x3y4+x4y5+x5y1−(y1x2+y2x3+y3x4+y4x5+y5x1)|
Substituting the coordinates of points A,B,C,D,E:
- (x1,y1)=(0,0)
- (x2,y2)=(2t2,0)
- (x3,y3)=(18,2)
- (x4,y4)=(8r2,4)
- (x5,y5)=(0,2)
Substituting into the area formula:
Area=12∣∣∣0⋅0+2t2⋅2+18⋅4+8r2⋅2+0⋅0−(0⋅2t2+0⋅18+2⋅8r2+4⋅0+2⋅0)∣∣∣
This simplifies to:
Area=12∣∣∣0+4t2+72+16r2+0−(0+0+16r2+0+0)∣∣∣
=12∣∣4t2+72∣∣
=2t2+36
To maximize the area 2t2+36, we can observe that as t increases, the area increases. However, we need to ensure that the angle at B is ≥90∘.
The angle at B will be ≥90∘ if the slopes of lines AB and BC satisfy:
slope of AB⋅slope of BC≤−1
Calculating the slopes:
- Slope of AB=0−02t2−0=0
- Slope of BC=2−018−2t2=218−2t2
Substituting t2=9 into the area formula:
Area=2(9)+36=18+36=54
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:JEE Main
Explore 6 Videos
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Matrix match type
Explore 4 Videos
- COORDINATE SYSTEMBook:CENGAGE ENGLISHChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGE ENGLISHChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
Knowledge Check
In the rectangular coordinate system shown, ABCD is a parallogram. If the coordinates of the points A,B,C and D are (0,2),(a,b),(a,2) and (0,0), respectively, then b =
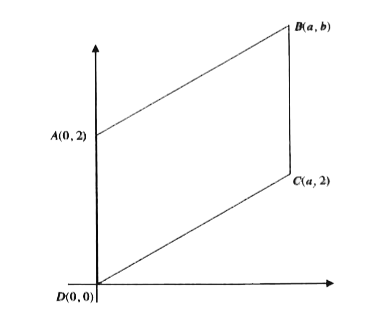 A0B2C3D4
A0B2C3D4
The points A(3,0) , B (a, -2) and C(4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
View SolutionPlot the points A(2,0),B(8,0),C(8,4). Complete the rectangle ABCD and find the co-ordinates of point D.
View SolutionThe coordinates of the fourth vertex of the rectangle formed by the points (0, 0), (2, 0), (0, 3) are (a) (3, 0) (b) (0, 2) (c) (2, 3) (d) (3, 2)
View SolutionThe point on the curve x2=2ywhich is nearest to the point (0, 5) is(A) (2√2,4) (B) (2√2,0) (C) (0, 0) (D) (2, 2)
View SolutionThe coordinates of the circumcentre of the triangle formed by the points O (0, 0) , A(a, 0) and B(0, b) are (a, b) (b) (a2,b2) (c) (b2,a2) (d) (b, a)
View SolutionShow that ΔABC, where A(−2,0),B(2,0),C(0,2)andΔPQR where P(−4,0),Q(4,0)andR(0,4) are similar triangles.
View SolutionStatement-1: The orthocentre of the triangle having its verticews at A(2,0), B(4,0) and C(4,6) is at the point o(4,0)
Statement-2 : Orthocentre of a right triangle is at the vertex forming a right angle
View Solution