In the given figure, OABC is a rectangle. Slope of OB is
 a. 1/4
b. 1/3
c. 1/2
d. Cannot be determined
a. 1/4
b. 1/3
c. 1/2
d. Cannot be determined
1/4
1/3
1/2
Cannot be determined
The correct Answer is:C
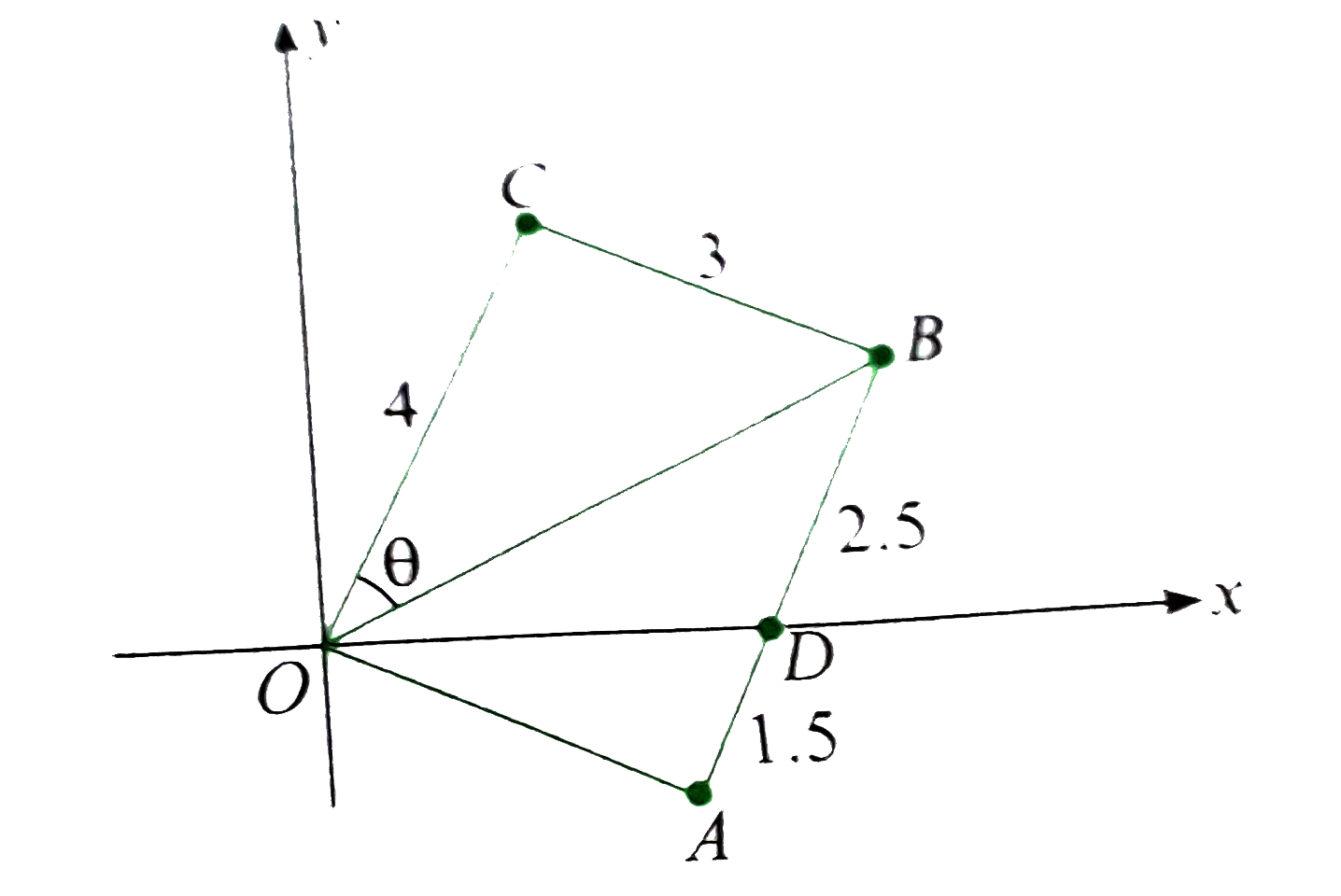
Clearly, OB=5
So, OAOB=35=1.52.5=ADDB
Thus, OD bisects ∠AOB.
Let ∠BOC=θ. Then tanθ=34
∴∠BOC=12∠AOB=12(90∘−θ)
∴ Slope of OB=tan(1)2(90∘−θ)=tan45∘−tan.θ21+tan45∘+tan.θ2
Now, tanθ=34
⇒2tan.θ21−tan2.θ2=34
3−3tan2.θ2=8tan.θ2
⇒3tan2.θ2+8tan.θ2−3=0
⇒(3tan.θ2−1)(tan.θ2+3)=0
So, tan.θ2=13 (∵θ2is acute)
∴ Slope of OB=1−131+13=12
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
In Figure, AB∣∣CD. Determine ∠1
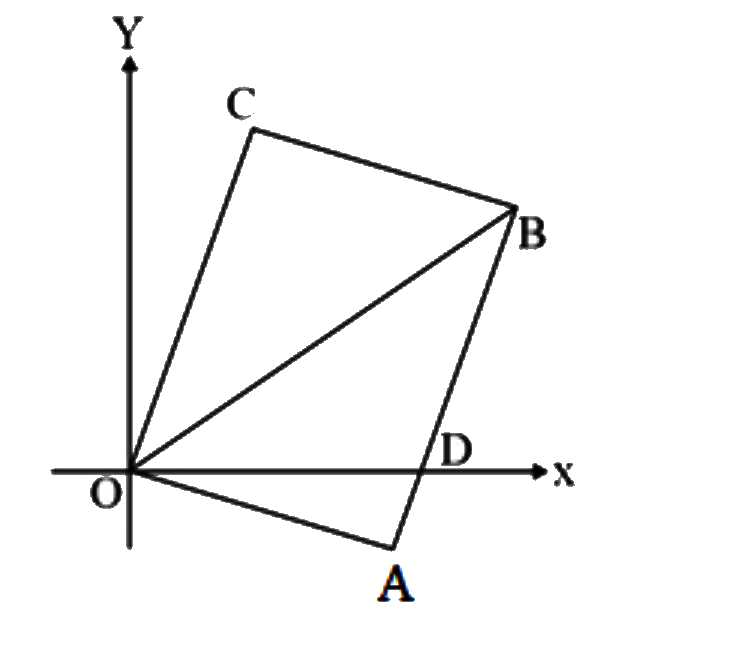
View SolutionIn the figure shown, OABC is a rectangle with OA=3 units, OC = 4 units. If BD = 2.5 units, then the slope of the diagonal OB is equal to
View SolutionPoint A and B are in the first quadrant,point O is the origin. If the slope of OA is 1,slope of OB is 7 and OA=OB,Then slope of AB is: a. -1/5 b. -1/4 c. -1/3 d. -1/2
View SolutionIn the given figure, AB || CD and ∠1 and ∠2 are in the ratio 3:2. Determine all angles from 1 to 8.
View SolutionIn the given figure, AC⊥CE and ∠A:∠B:∠C=3:2:1, find the value of ∠ECD.
View SolutionA four figure number is formed of the figures 1, 2, 3, 4, 5 with no repetitions. The probability that the number is divisible by 5 is 3/4 b. 1/4 c. 1/8 d. none of these
View SolutionPoint A and B are in the first quadrant; point O is the origin. If the slope of OA is 1, the slope of OB is 7, and OA=OB, then the slope of AB is −15 (b) −14 (c) −13 (d) −12
View SolutionA(1, 3) and C(5, 1) are two opposite vertices of a rectangle ABCD. If the slope of BD is 2, then the coordinates of B can be :
View SolutionThe number of lines of symmetry of a rectangle is (a) 2 (b) 3 (c) 4 (d) 1
View SolutionABCD is a rectangle with ∠ABD=400. Determine ∠DBC
View Solution
