Consider a point A(m,n) , where m and n are positve intergers. B is the reflection of A in the line y=x, C is the reflaction of B in the y axis, D is the reflection of C in the x axis and E is the reflection of D is the y axis. The area of the pentagon ABCDE is a. 2m(m+n) b. m(m+3n) c. m(2m+3n) d. 2m(m+3n)
2m(m+n)
m(m+3n)
m(2m+3n)
2m(m+3n)
The correct Answer is:B
To solve the problem, we will follow the steps outlined in the video transcript and derive the area of the pentagon ABCDE.
1. Identify the Coordinates of Point A:
- Let point A be A(m,n), where m and n are positive integers.
2. Find the Coordinates of Point B:
- Point B is the reflection of A across the line y=x.
- The coordinates of point B will be B(n,m).
3. Find the Coordinates of Point C:
- Point C is the reflection of B across the y-axis.
- The coordinates of point C will be C(−n,m).
4. Find the Coordinates of Point D:
- Point D is the reflection of C across the x-axis.
- The coordinates of point D will be D(−n,−m).
5. Find the Coordinates of Point E:
- Point E is the reflection of D across the y-axis.
- The coordinates of point E will be E(n,−m).
6. Plot the Points:
- The coordinates of the points are:
- A(m,n)
- B(n,m)
- C(−n,m)
- D(−n,−m)
- E(n,−m)
7. Divide the Pentagon into Shapes:
- The pentagon ABCDE can be divided into a rectangle and a triangle.
- The rectangle is formed by points A, B, D, and E.
- The triangle is formed by points A, C, and D.
8. Calculate the Area of the Rectangle:
- The length of the rectangle is 2m (from A to E).
- The height of the rectangle is 2n (from A to D).
- Area of the rectangle = Length × Height = 2m×2n=4mn.
9. Calculate the Area of the Triangle:
- The base of the triangle (AC) is 2m (from A to C).
- The height of the triangle is m−n (vertical distance from A to C).
- Area of the triangle = 12×Base×Height=12×2m×(m−n)=m(m−n).
10. Total Area of Pentagon ABCDE:
- Total Area = Area of Rectangle + Area of Triangle
- Total Area = 4mn+m(m−n)=4mn+m2−mn=m2+3mn.
11. Final Expression:
- The total area can be factored as m(m+3n).
Conclusion:
The area of the pentagon ABCDE is given by m(m+3n).
- Let point A be A(m,n), where m and n are positive integers.
- Point B is the reflection of A across the line y=x.
- The coordinates of point B will be B(n,m).
- Point C is the reflection of B across the y-axis.
- The coordinates of point C will be C(−n,m).
- Point D is the reflection of C across the x-axis.
- The coordinates of point D will be D(−n,−m).
- Point E is the reflection of D across the y-axis.
- The coordinates of point E will be E(n,−m).
- The coordinates of the points are:
- A(m,n)
- B(n,m)
- C(−n,m)
- D(−n,−m)
- E(n,−m)
- The pentagon ABCDE can be divided into a rectangle and a triangle.
- The rectangle is formed by points A, B, D, and E.
- The triangle is formed by points A, C, and D.
- The length of the rectangle is 2m (from A to E).
- The height of the rectangle is 2n (from A to D).
- Area of the rectangle = Length × Height = 2m×2n=4mn.
- The base of the triangle (AC) is 2m (from A to C).
- The height of the triangle is m−n (vertical distance from A to C).
- Area of the triangle = 12×Base×Height=12×2m×(m−n)=m(m−n).
- Total Area = Area of Rectangle + Area of Triangle
- Total Area = 4mn+m(m−n)=4mn+m2−mn=m2+3mn.
- The total area can be factored as m(m+3n).
The area of the pentagon ABCDE is given by m(m+3n).
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Let m,n are integers with 0<n<m. A is the point (m,n) on the Cartesian plane. B is the reflection of A in the line y=x. C is the reflection of B in the y-axis, D is the reflection of C in the x-axis and E is the reflection of D in the y-axis. The area of the pentagon ABCDE is
a.2m(m+n) b. m(m+3n) c. m(2m+3n) d. 2m(m+3n)
View SolutionLet m,n are integers with 0<n<m. A is the point (m,n) on the Cartesian plane. B is the reflection of A in the line y=x. C is the reflection of B in the y-axis. D, is the reflection of C in the x-axis and E is the reflection of D in the y-axis. The area of the pentagon ABCDE is 2m(m+n) (b) m(m+3n) m(2m+3n) (d) 2m(m+3n)
View SolutionIf is the line whose equation is ax+by=c. Let M be the reflection of 'L through the y-axis and let N be the reflection of L through the x-axis. Which of the following must be true about M and N for choices of a,b and c?
View SolutionM and N are two points on the X-axis and Y-axis respectively. P(3, 2) divides the line segment MN in the ratio 2:3.
Find :
(i) the coordinates of M and N
View SolutionFind the values of m and n, in each case, If:
(4,−3) on reflection in x-axis gives (−m,n).
View Solution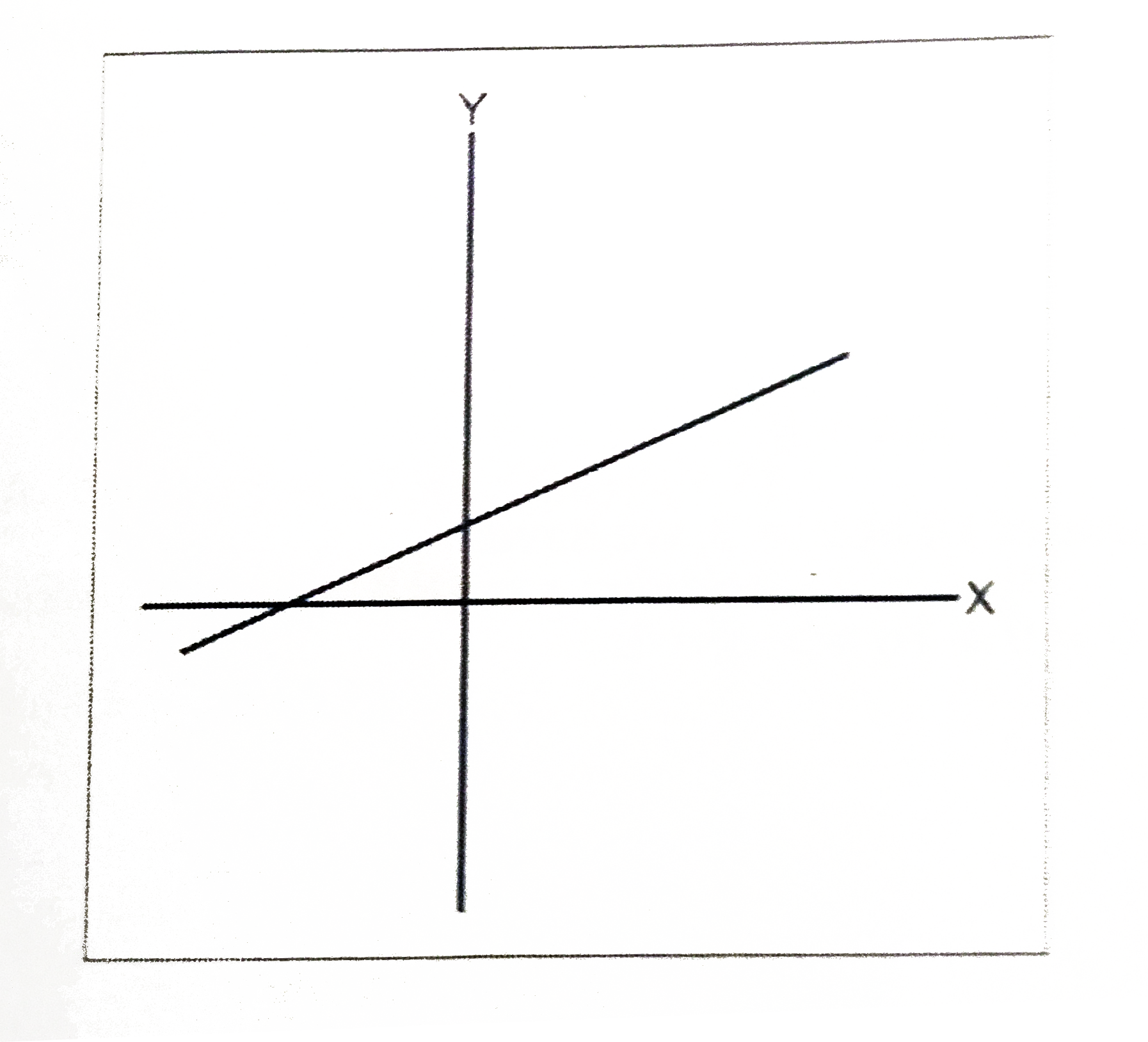
The graph below depicts the straight line y=x2+3. If the line is reflected about the X axis and the equation of the new lines is y=mx+n, what is the value of |m+n| ?
View SolutionFind the values of m and n, in each case, If:
(m,5) on reflection iny-axis gives (−5,n−2)
View SolutionStraight lines are drawn by joining m points on a straight line of n points on another line. Then excluding the given points, the number of point of intersections of the lines drawn is (no tow lines drawn are parallel and no these lines are concurrent). a. 4mn(m−1)(n−1) b. 12mn(m−1)(n−1) c. 12m2n2 d. 14m2n2
View SolutionIf a, m, n are positive integers, then {m√n√a}mn is equal to
(a) amn
(b) a
(c) amn
(d) 1
View SolutionThe perpendicular from the origin to the line y=mx+c meets it at the point (-1,2). Find the values of m and c.
View Solution
