Let ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD:2x+y=3. If length of diagonal AC=4 units and area of ABCD=8 sq. units. Then
(i) The length of the other diagonal is
(ii) the length of side AB is equal to
The correct Answer is:A
To solve the problem step by step, we will follow the information given and the properties of parallelograms.
Step 1: Identify the equations of the diagonals
The equations of the diagonals are given as:
- Diagonal AC: x+2y=3
- Diagonal BD: 2x+y=3
Step 2: Find the slopes of the diagonals
To find the slopes, we can rewrite the equations in slope-intercept form y=mx+c.
For diagonal AC:
x+2y=3⟹2y=−x+3⟹y=−12x+32
Thus, the slope m1 of diagonal AC is −12.
For diagonal BD:
2x+y=3⟹y=−2x+3
Thus, the slope m2 of diagonal BD is −2.
Step 3: Calculate the angle between the diagonals
The angle θ between the two lines can be found using the formula:
tanθ=m1−m21+m1m2
Substituting the values of m1 and m2:
tanθ=−12−(−2)1+(−12)(−2)=−12+21+1=322=34
Step 4: Find sinθ
Using the Pythagorean theorem, we can find sinθ:
If tanθ=34, then we can form a right triangle where the opposite side is 3 and the adjacent side is 4. The hypotenuse h is:
h=√32+42=√9+16=5
Thus,
sinθ=35
Step 5: Use the area formula of the parallelogram
The area A of the parallelogram can be expressed in terms of the diagonals:
A=12×AC×BD×sinθ
We know:
- A=8
- AC=4
- sinθ=35
Substituting these values into the area formula:
8=12×4×BD×35
Simplifying:
8=25×BD⟹BD=8×52=20
Step 6: Find the length of side AB
Using the property of triangles, we can find the length of side AB. The diagonals bisect each other, so:
- AO=OC=2 (since AC=4)
- BO=OD=10/3 (since BD=20/3)
Using the cosine rule:
cosθ=AO2+OB2−AB22⋅AO⋅OB
We know sinθ=35, hence cosθ=√1−sin2θ=45.
Substituting the values:
45=22+(103)2−AB22⋅2⋅103
Calculating:
45=4+1009−AB2403⟹4⋅403=5(4+1009−AB2)
Simplifying:
1603=20+5009−5AB2
Clearing fractions and solving for AB2:
160⋅93=60+500−45AB2
480=60+500−45AB2⟹45AB2=60+500−480⟹45AB2=80⟹AB2=8045=169
Thus,
AB=43
Final Answers
(i) The length of the other diagonal BD=203 units.
(ii) The length of side AB=43 units.
The equations of the diagonals are given as:
- Diagonal AC: x+2y=3
- Diagonal BD: 2x+y=3
To find the slopes, we can rewrite the equations in slope-intercept form y=mx+c.
x+2y=3⟹2y=−x+3⟹y=−12x+32
Thus, the slope m1 of diagonal AC is −12.
2x+y=3⟹y=−2x+3
Thus, the slope m2 of diagonal BD is −2.
The angle θ between the two lines can be found using the formula:
tanθ=m1−m21+m1m2
Substituting the values of m1 and m2:
tanθ=−12−(−2)1+(−12)(−2)=−12+21+1=322=34
Using the Pythagorean theorem, we can find sinθ:
If tanθ=34, then we can form a right triangle where the opposite side is 3 and the adjacent side is 4. The hypotenuse h is:
h=√32+42=√9+16=5
Thus,
sinθ=35
The area A of the parallelogram can be expressed in terms of the diagonals:
A=12×AC×BD×sinθ
We know:
- A=8
- AC=4
- sinθ=35
8=12×4×BD×35
Simplifying:
8=25×BD⟹BD=8×52=20
Using the property of triangles, we can find the length of side AB. The diagonals bisect each other, so:
- AO=OC=2 (since AC=4)
- BO=OD=10/3 (since BD=20/3)
cosθ=AO2+OB2−AB22⋅AO⋅OB
We know sinθ=35, hence cosθ=√1−sin2θ=45.
45=22+(103)2−AB22⋅2⋅103
Calculating:
45=4+1009−AB2403⟹4⋅403=5(4+1009−AB2)
Simplifying:
1603=20+5009−5AB2
Clearing fractions and solving for AB2:
160⋅93=60+500−45AB2
480=60+500−45AB2⟹45AB2=60+500−480⟹45AB2=80⟹AB2=8045=169
Thus,
AB=43
(i) The length of the other diagonal BD=203 units.
(ii) The length of side AB=43 units.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (MATRIX MATCH TYPE)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (NUMERICAL VALUE TYPE)
Explore 13 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
Explore 30 Videos
- STRAIGHT LINEBook:CENGAGE ENGLISHChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
Let ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD: 2x + y = 3. If length of diagonalAC=4 units and area of ABCD=8 sq. units. Find the length of the other diagonal is a. 10/3 b. 2 c. 20/3 d. None of these
View SolutionABCD is a parallelogram. x + 2y = 3 and 2x + y = 3 are the equations of the diagonals AC and BD respectively. AC = 4 units and area of parallelogram ABCD is 8 sq. units then The length of BC is equal to
View SolutionIn a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
View SolutionThree vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find :
(ii) length of diagonal BD.
View SolutionConstruct a rectangle ABCD, when :
One side = 4cm and one diagonal is 5cm. Measure the length of other side.
View SolutionFind lengths of diagonals AC and BD. Given AB = 60 cm and ∠BAD=60∘.
View SolutionIn rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
View SolutionThe point (−4,5) is vertex of a square and one of its diagonal is 7x−y+8=0. The equation of other diagonal is
View SolutionThe area of a rhombus is 243 cm2 .If one of the diagonals is 19.5 cm long , find the length of the other diagonal.
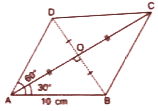
View SolutionIn a rhombus ABCD, length of each side is 10 cm and ∠A=60∘. Find the lengths of its diagonals AC and BD.
View Solution

