Let ABCD be a parallelogram the equation of whose diagonals are ; BD: 2x + y = 3. If length of diagonal units and area of sq. units. Find the length of the other diagonal is a. b. c. d. None of these
2
none of these
The correct Answer is:C
To find the length of the other diagonal BD of the parallelogram ABCD, we will follow these steps:
Step 1: Understand the properties of the parallelogram
In a parallelogram, the diagonals bisect each other. This means that if O is the intersection point of the diagonals AC and BD, then:
- OA=OC
- OB=OD
Step 2: Use the area of the parallelogram
The area of parallelogram ABCD can be expressed in terms of the lengths of the diagonals and the sine of the angle θ between them:
Area=12×AC×BD×sin(θ)
Given that the area is 8 square units and the length of diagonal AC is 4 units, we can substitute these values into the equation:
8=12×4×BD×sin(θ)
This simplifies to:
8=2×BD×sin(θ)
BD×sin(θ)=4(Equation 1)
Step 3: Find the slopes of the diagonals
The equations of the diagonals are given as:
- AC:x+2y=3
- BD:2x+y=3
To find the slopes, we can rewrite these equations in slope-intercept form y=mx+b.
For AC:
2y=−x+3⟹y=−12x+32⇒slope m1=−12
For BD:
y=−2x+3⇒slope m2=−2
Step 4: Calculate the angle between the diagonals
The angle θ between the two lines can be found using the formula:
tan(θ)=m2−m11+m1m2
Substituting the slopes:
tan(θ)=−2−(−12)1+(−12)(−2)=−2+121+1=−42+122=−322=−34
Step 5: Find sin(θ)
Using the identity sin2(θ)+cos2(θ)=1:
Let sin(θ)=35 and cos(θ)=45 (from the right triangle formed).
Step 6: Substitute sin(θ) back into Equation 1
Now we can substitute sin(θ) back into Equation 1:
BD×35=4
Solving for BD:
BD=4×53=203
Conclusion
Thus, the length of the other diagonal BD is 203.
In a parallelogram, the diagonals bisect each other. This means that if O is the intersection point of the diagonals AC and BD, then:
- OA=OC
- OB=OD
The area of parallelogram ABCD can be expressed in terms of the lengths of the diagonals and the sine of the angle θ between them:
Area=12×AC×BD×sin(θ)
Given that the area is 8 square units and the length of diagonal AC is 4 units, we can substitute these values into the equation:
8=12×4×BD×sin(θ)
This simplifies to:
8=2×BD×sin(θ)
BD×sin(θ)=4(Equation 1)
The equations of the diagonals are given as:
- AC:x+2y=3
- BD:2x+y=3
2y=−x+3⟹y=−12x+32⇒slope m1=−12
y=−2x+3⇒slope m2=−2
The angle θ between the two lines can be found using the formula:
tan(θ)=m2−m11+m1m2
Substituting the slopes:
tan(θ)=−2−(−12)1+(−12)(−2)=−2+121+1=−42+122=−322=−34
Using the identity sin2(θ)+cos2(θ)=1:
Let sin(θ)=35 and cos(θ)=45 (from the right triangle formed).
Now we can substitute sin(θ) back into Equation 1:
BD×35=4
Solving for BD:
BD=4×53=203
Thus, the length of the other diagonal BD is 203.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)
8 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (NUMERICAL VALUE TYPE)
13 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Let ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD:2x+y=3. If length of diagonal AC=4 units and area of ABCD=8 sq. units. Then
(i) The length of the other diagonal is
(ii) the length of side AB is equal to
View SolutionABCD is a parallelogram. x + 2y = 3 and 2x + y = 3 are the equations of the diagonals AC and BD respectively. AC = 4 units and area of parallelogram ABCD is 8 sq. units then The length of BC is equal to
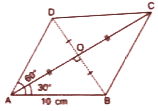
View SolutionIn a rhombus ABCD, length of each side is 10 cm and ∠A=60∘. Find the lengths of its diagonals AC and BD.
View SolutionThe equation of one diagonal of a square is 2x+y=6 and its one vertex is (4,3). Find the equation of other diagonal.
View SolutionThe length of the diagonals of a rhombus is 16 cm. If its area is 96 cm2, then the length of other diagonal is (a)6 cm (b) 8 cm (c)10 cm (d) 18 cm
View SolutionABCD is a rhombus whose diagonals intersect at O. If AB=10cm, diagonals BD=16 cm , find the length of diagonal AC
View SolutionIn rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
View SolutionThree vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find :
(ii) length of diagonal BD.
View SolutionConstruct a parallelogram ABCD in which diagonal AC = 6-3 cm, diagonal BD = 7cm and the acute angles between the diagonals is 45°
View SolutionThe equation of the diagonals of a rectangle are y+8x−17=0 and y−8x+7=0. If the area of the rectangle is 8squnits then find the sides of the rectangle
View Solution
