The coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively. The equation of the diagonal CE is:
√3x+y=4
x+√3y+4=0
x+√3y=4
none of these
The correct Answer is:C
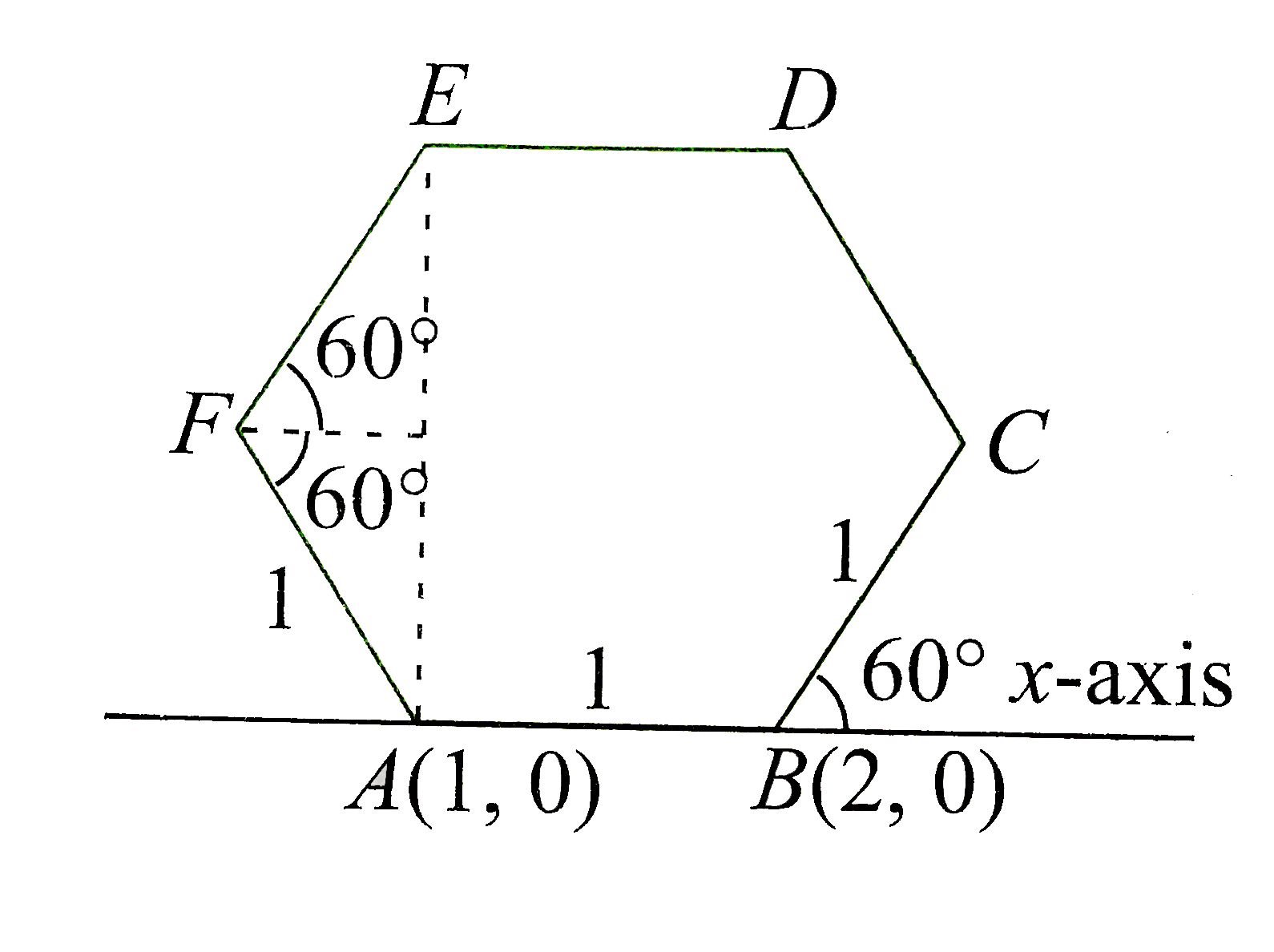
AB=1
or C≡(2+1×cos60∘,1×sin60∘)≡(52,√32)
E≡(1,1×sin60∘+1×sin60∘)≡(1,√3)
Therefore, the equation of CE is
y−√3=−1√3(x−1)
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
Explore 30 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGE ENGLISHChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
The coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is (a)√3x+y=4 (b) x+√3y+4=0 (c)x+√3y=4 (d) none of these
View Solutiona and b form the consecutive sides of a regular hexagon ABCDEF.

View SolutionThe coordinates of the vertices BandC of a triangle ABC are (2, 0) and (8, 0), respectively. Vertex A is moving in such a way that 4tanB2tanC2=1. Then find the locus of A
View SolutionThe coordinates of three consecutive vertices of a parallelogram are (1, 3), (-1, 2) and (2, 5). Then find the coordinates of the fourth vertex.
View SolutionThe vertices of ΔABC are A(−3,2), B(0,3) and C(1,0). Find the equation of the median through B.
View SolutionIf the vertices A,B,C of a triangle ABC are (1,2,3),(-1,0,0) ,(0,1,2) , respectively, then find ∠ABC.
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Find the area of the rectangle and the equation of that diagonal of the rectangle which passes through the point (2,4).
View SolutionThe sides AB and AD of a parallelogram ABCD are 2x−y+1=0andx+3y−10=0 respectively and C is the point (−1,−2). Find the equation of the diagonals AC.
View SolutionIn a triangle, ABC, the equation of the perpendicular bisector of AC is 3x−2y+8=0. If the coordinates of the points A and B are (1,−1)&(3,1) respectively, then the equation of the line BC & the centre of the circum-circle of the triangle ABC will be
View SolutionThe experimities of the diagonal of a square are (1,1) ,(−2,−1) .Obtain the other two vertices and the equation of the other diagonal .
View Solution

