The equation of a straight line on which the length of perpendicular from the origin is four units and the line makes an angle of with the x-axis is (a) (b) (c) (d)
The correct Answer is:A
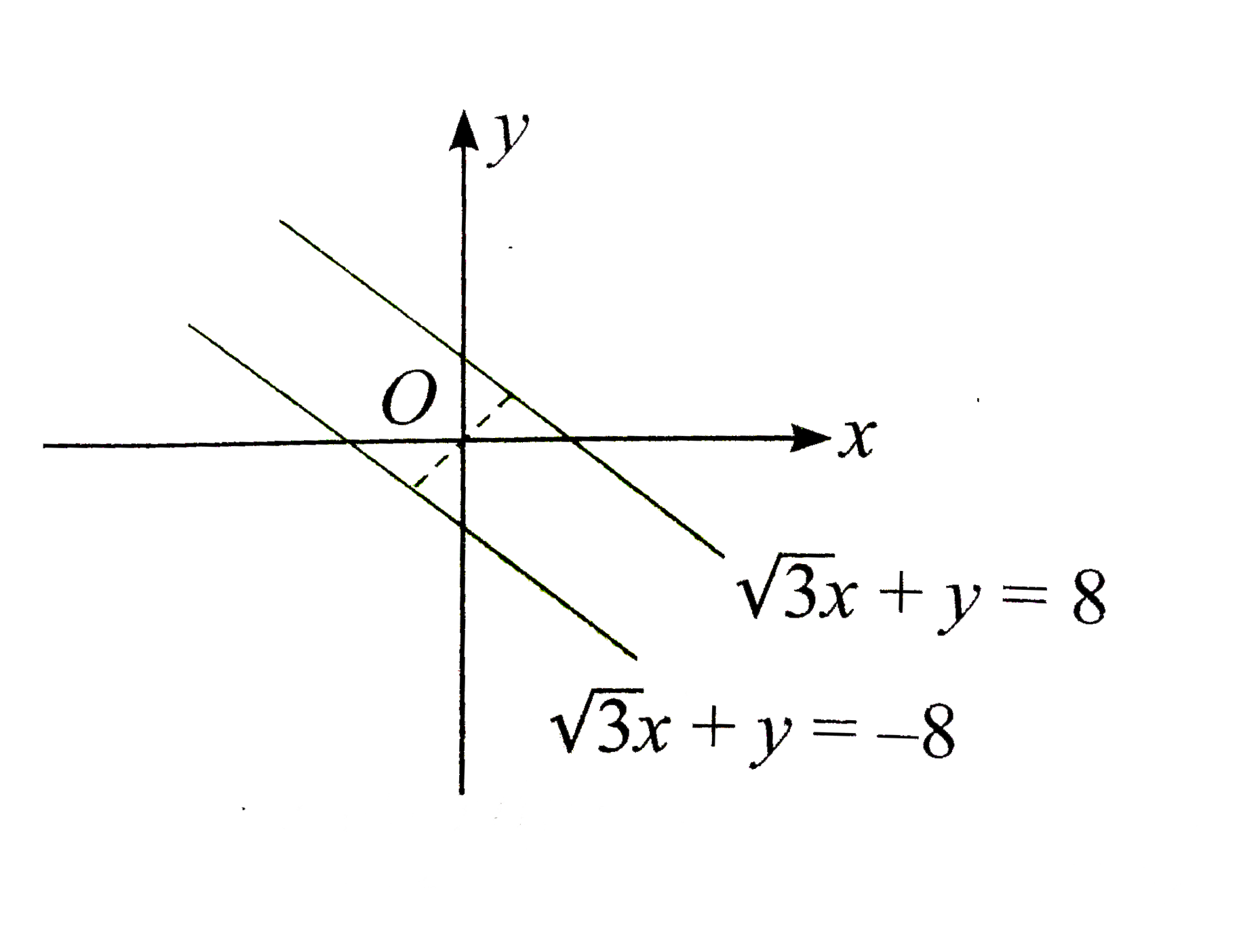
Given that the slope is .
Therefore, the line is
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
Explore 30 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGE ENGLISHChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
a Find equation of a straight line on which length of perpendicular from the origin is four units and the line makes an angle of 1200 with the positive direction of x-axis.
View SolutionFind the equation of the straight line on which the length of the perpendicular from the origin is 4 units and the line makes an angle of 1200 with positive direction of x-axis
View Solution
Knowledge Check
The equation of a straight line on which the perpendicular from the origin of the length 2 units and this perpendicular makes an angle of 240∘ with the x-axis is (i) x+√3y+4=0 (ii) x−√3y+4=0 (iii) x−√3y−4=0 (iv) x+√3y−4=0
Ax+√3y+4=0Bx−√3y+4=0Cx−√3y−4=0Dx+√3y−4=0
Find the equation of the straight line upon which the length of perpendicular from origin is 3√2 units and this perpendicular makes an angle of 750 with the positive direction of x-axis.
View SolutionThe equation of line on which the perpendicular from the origin make 300 angle with the x-axis and which form a triangle of area 50√3 with the axes is a. √3x+y−10=0 b. √3x+y+10=0 c. x+√3y−10=0 d. x−√3y−10=0
View SolutionFor the straight line 8x−15y+51=0, find the length of the perpendicular from the origin to this line and the inclination of this perpendicular with the x-axis.
View SolutionFind the slope of a line perpendicular to the line 3x+5y=8.
View SolutionThe equation of the tangent to the parabola y2=8x which is perpendicular to the line x−3y+8=0, is
View SolutionReduce each of the equations to the normal form and find the length of the perpendicular from origin to the line √3x+y−8=0
View SolutionReduce each of the equations to the normal form and find the length of the perpendicular from origin to the line x−√3y+8=0
View Solution

