Question

Draw the graph of the function ${\displaystyle f\left(x\right)=x-|x-x^2|,-1\le x\le 1}$ and find the points of non-differentiability.

Explanation

We have `y= f(x)=x- |x-x^(2)|`
`" "= {{:(x-(x^(2)-x)",",,x^(2)-x ge0),(x-(x-x^(2))",",,x^(2)-x lt 0):}`
`" "= {{:(x-(2x-x^(2))",",,xle0 or x ge 1),(x^(2)",",,0ltxlt1):}`
The graph of the function `y= 2x-x^(2)= x(2-x)` is a downward parabola intersecting the x-axis at `x=0 and x=2`.
Thus, the graph of the function `y= f(x)` is as follows:

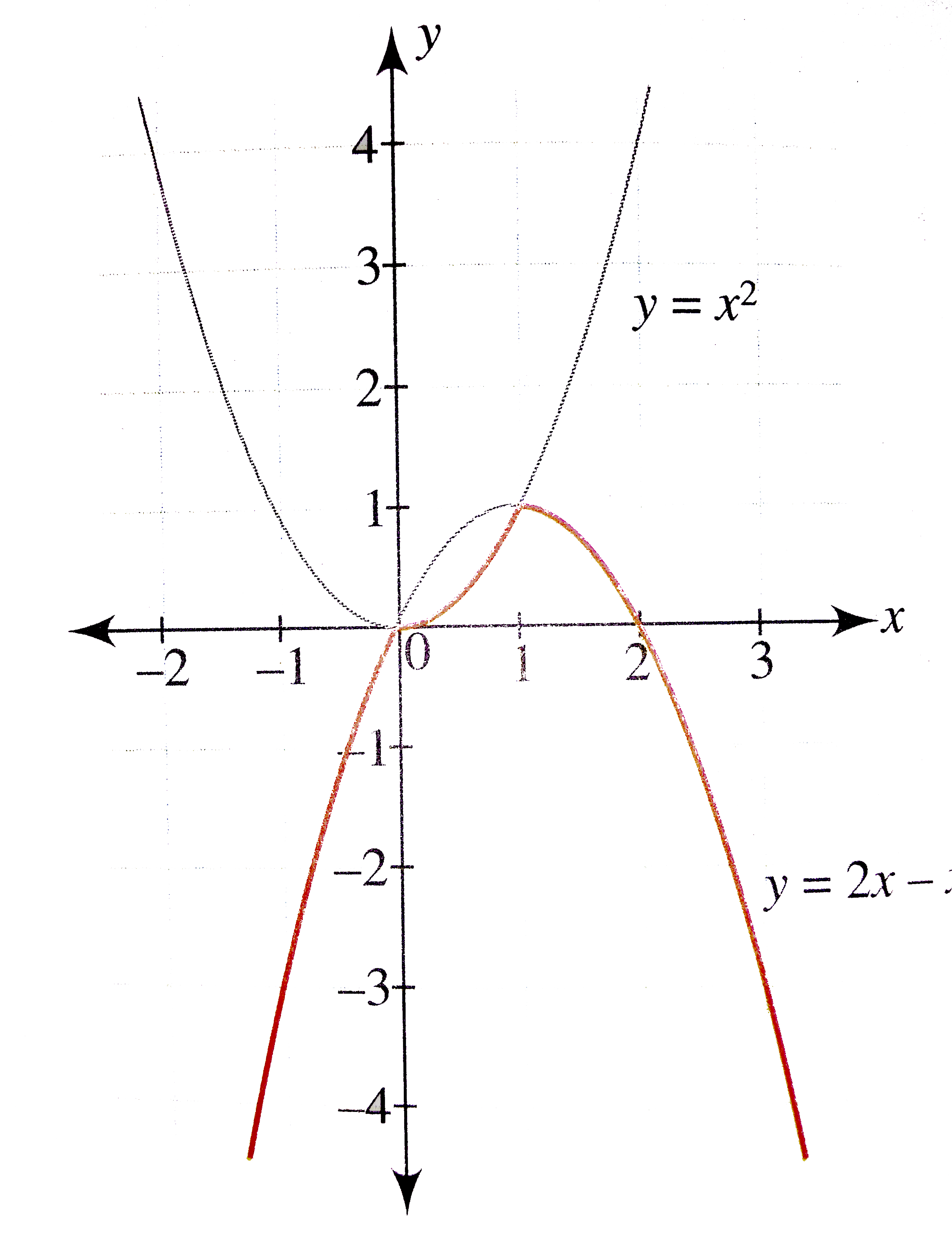
Clearly from the graph the function is continuous but non-differentiable at `x=0, 1`.