Let f(x)=(1−x)2sin2x+x2 for all x ∈ R, and let g(x)=∫(2(t−1)t+1−lnt)f(t)dt for t ∈ [1, x] for all x ∈ (1, ∞).Which of the following is true ?
Suppose A(x,f(x))andB(y,f(y)) be any two points on the curve y=f(x).
If M is the mid-point of AB, then the coordinates of M are (x+y2,f(x)+f(y)2).
Now the foot of the perpendicular from the M on the x-axis is L. ML meets the curve y=f(x) at P.
According to the graph, the coordinates of P are (x+y2,f(x+y2))andPL>ML.
⇒ f(x+y2)>f(x)+f(y)2
But given f(x+y2)=f(x)+f(y)2, which is possible when P→M.
That is, P lies on AB. Hence y=f(x) must be a linear function.
Let f(x)=ax+b ⇒f(0)=0+b=1 (given )
and f'(x)=a ⇒f'(0)=a=−1 (given )
∴ f(x)=−x+1
∴ f(2)=−2+1=−1
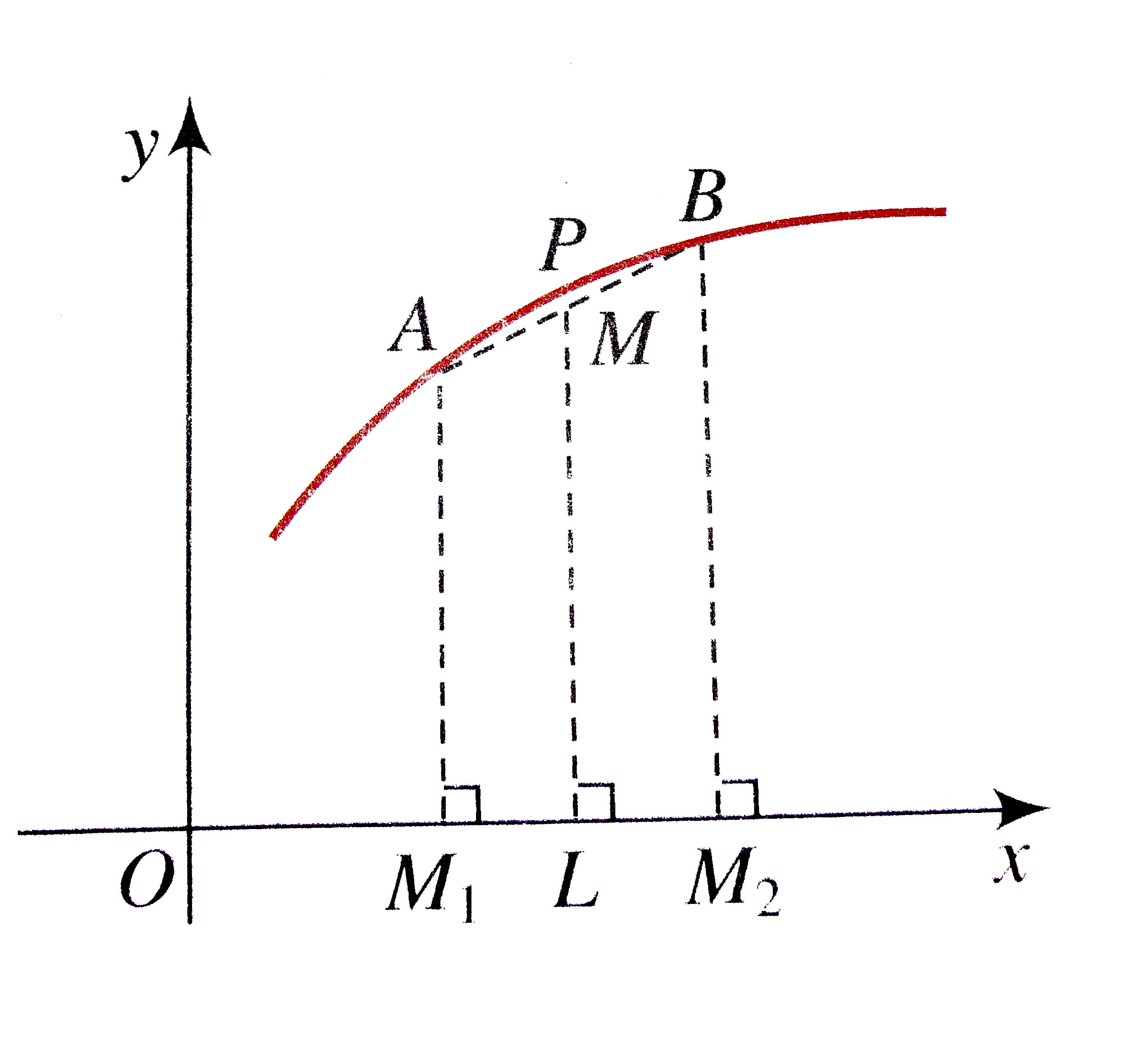
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
Let f(x)=(1−x)2sin2x+x2 for all x∈IR and let g(x)=∫x1(2(t−1)t+1−lnt)f(t) dt for all x∈(1,∞).
Which of the following is true ?
View SolutionLet f(x)=(1−x)2sin2x+x2 for all x∈IR and let g(x)=∫x1(2(t−1)t+1−lnt)f(t) dt for all x∈(1,∞).
Consider the statements :
P : There exists some x∈IR such that f(x)+2x=2(1+x2)
Q : There exist some x∈IR such that 2f(x)+1=2x(1+x)
Then
View Solution
Knowledge Check
For all t>0,f(x)=t2−1t−1−t . Which of the following is true about f(t) ?
AIt increases in proportion to t.BIt increases in proportion to t2.CIt decreases in proportion to t.DIt remains constant .
Let g(x)=∫ex0f'(t)dt1+t2. Which of the following is true?
View SolutionLet f(x)=∫x−2|t+1|dt, then
View SolutionLet f(x)=1x2∫x4(4t2−2f'(t)dt, find 9f'(4)
View SolutionLet f(x)=∫x3x2dtlnt for x>1andg(x)=∫x1(2t2−lnt)f(t)dt(x>1), then: (a) g is increasing on (1,∞) (b) g is decreasing on (1,∞) (c) g is increasing on (1,2) and decreasing on (2,∞) (d) g is decreasing on (1,2) and increasing on (2,∞)
View SolutionLet f(x)=∫x13t1+t2dt, where x>0, Then
View SolutionIf∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) , is
View Solutionf(x):[0,5]→R,F(x)=∫x0x2g(x), f(1) = 3
g(x) = ∫x1f(t)dt then correct choice is
View Solution
