For an ideal gas, an illustration of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
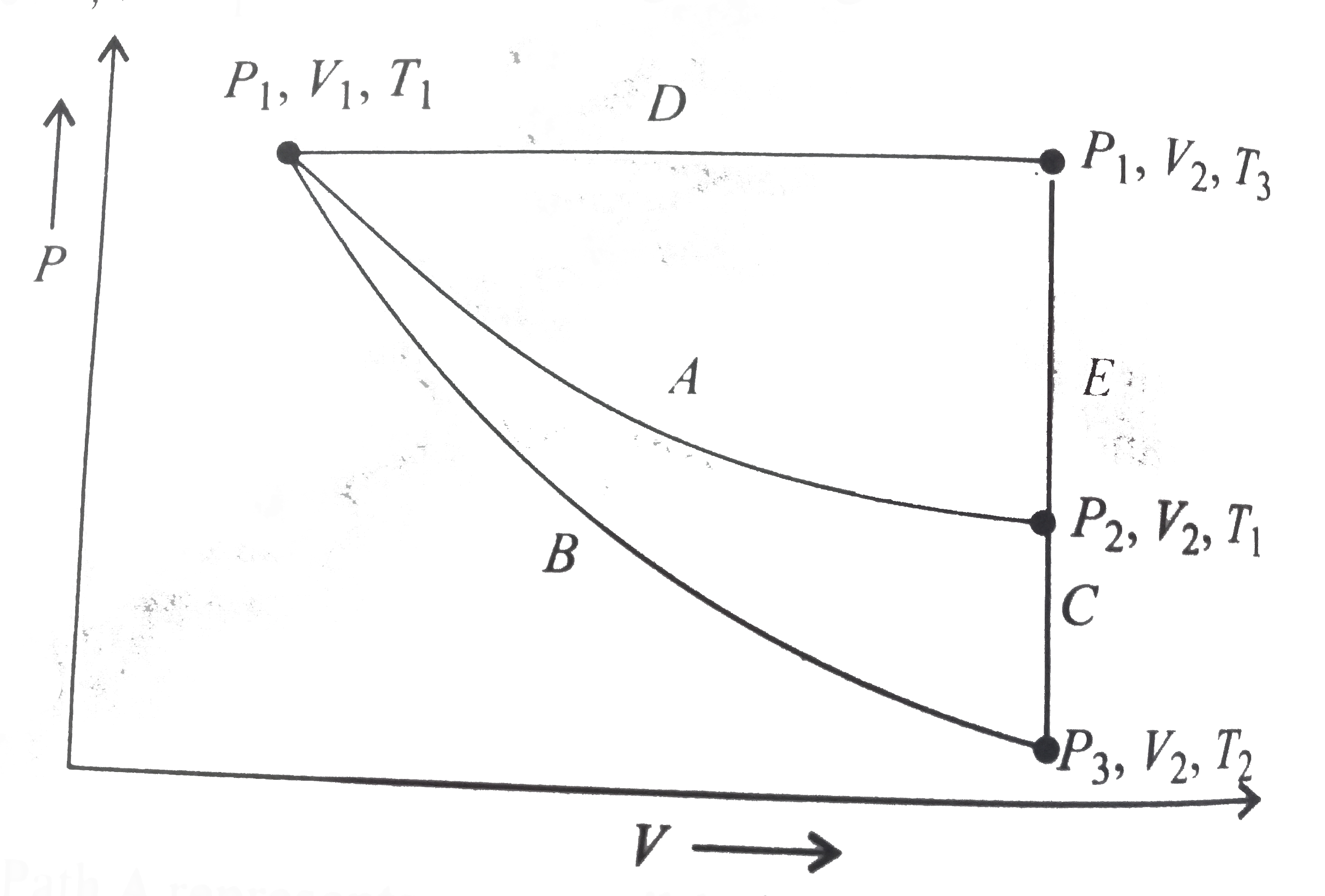
Path A represents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
Both the statements are true, and Statement 2 is the correct explanation for Statement 1.
Both the Statements are true, but Statement 2 is not the correct explanation for Statement 1.
Statement 1 is true and Statement 2 is false.
Statement 1 is false and Statement 2 is true.
The correct Answer is:d
Direction ratios of the given lines are (−3,1,−1)and(1,2,−1). Hence, the lines are perpendicular as (−3)(1)+(1)(2)+(−1)(−1)=0.
Also lines are coplanar as
∣∣
∣
∣∣0−21−3−1+(13/7)−31−112−1∣∣
∣
∣∣=0
But Statement 2 is not enough reason for the shortest distance to be zero, as two skew lines can also be perpendicular.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE
12 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE
17 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
Similar Questions
For an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
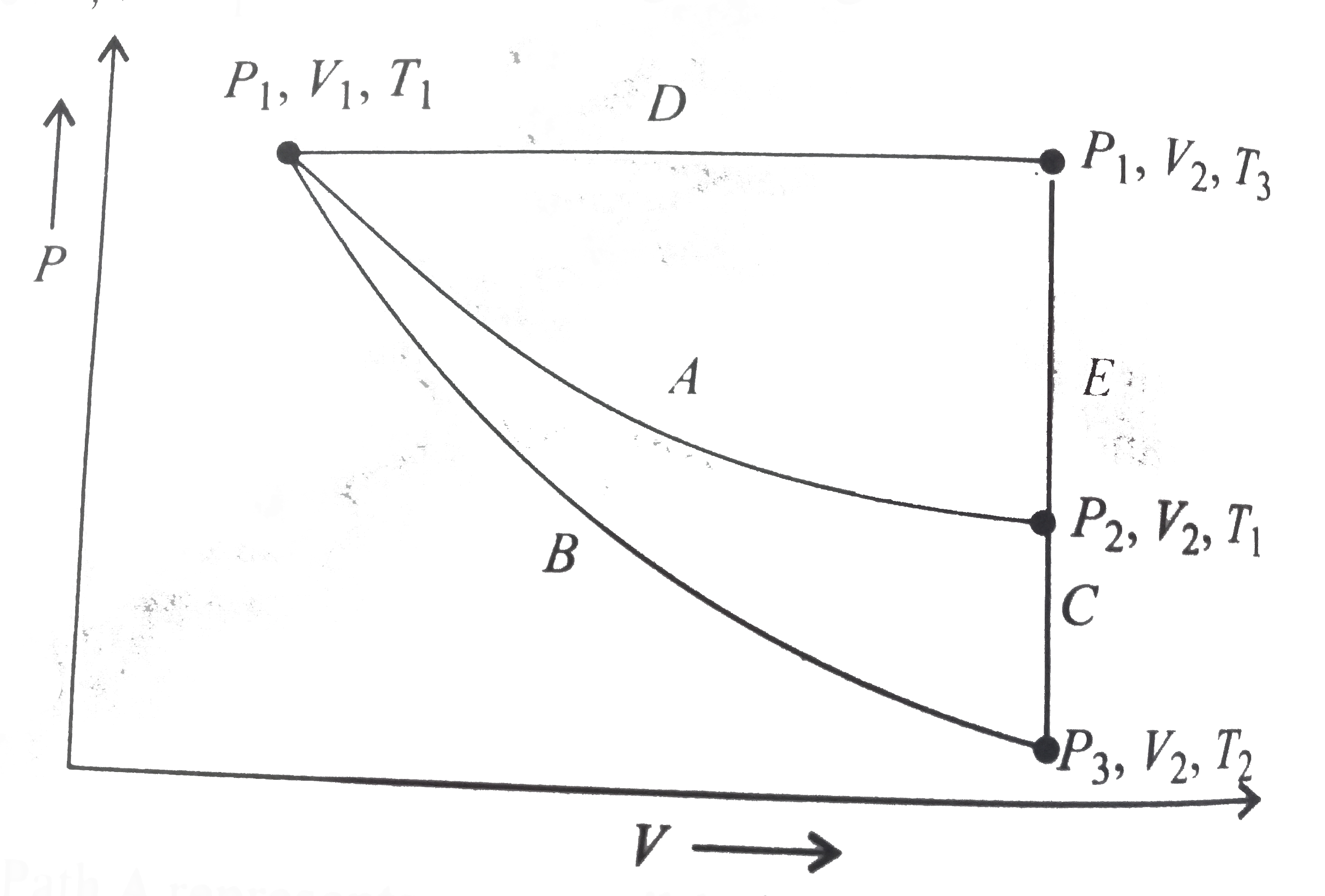
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
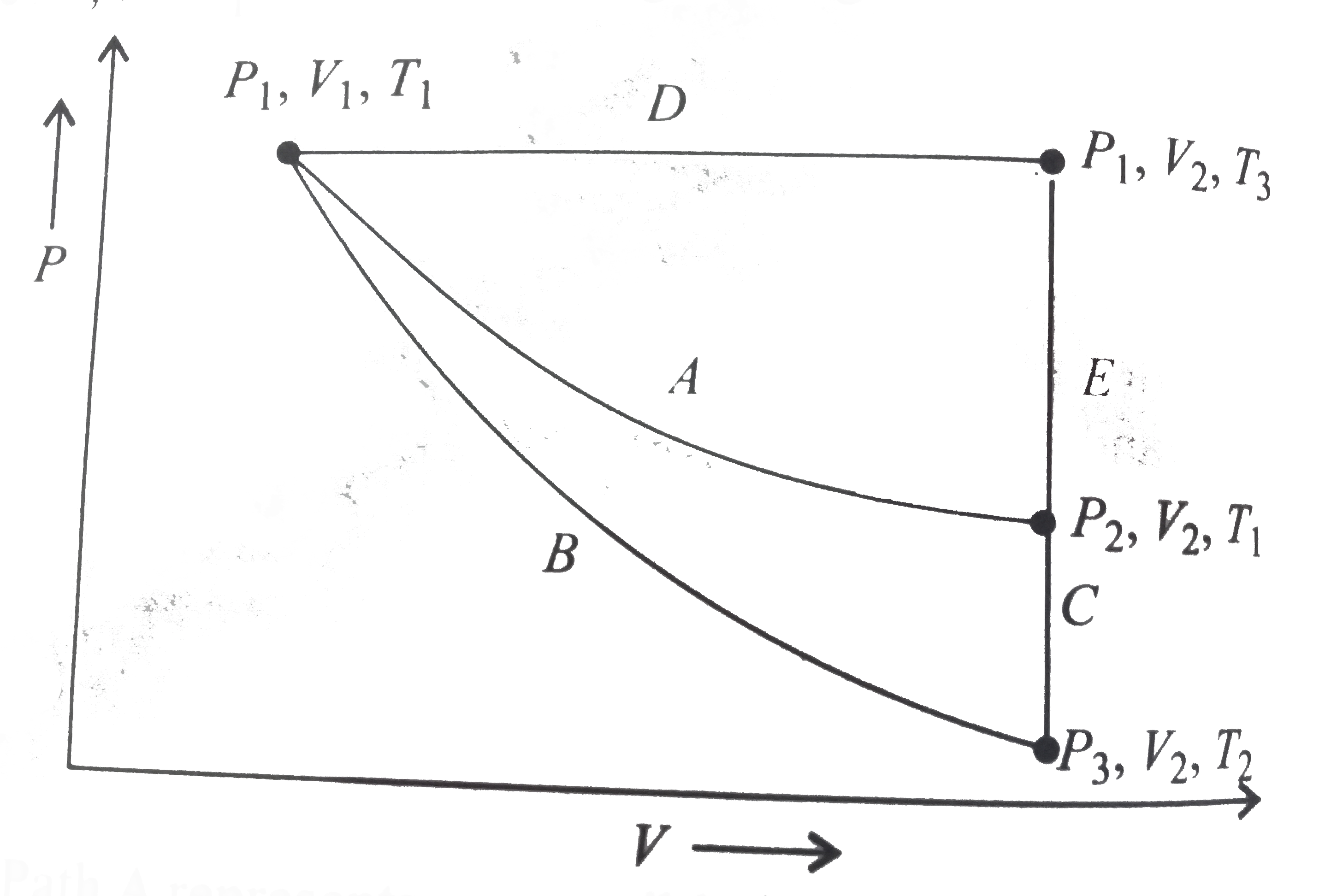
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionA gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
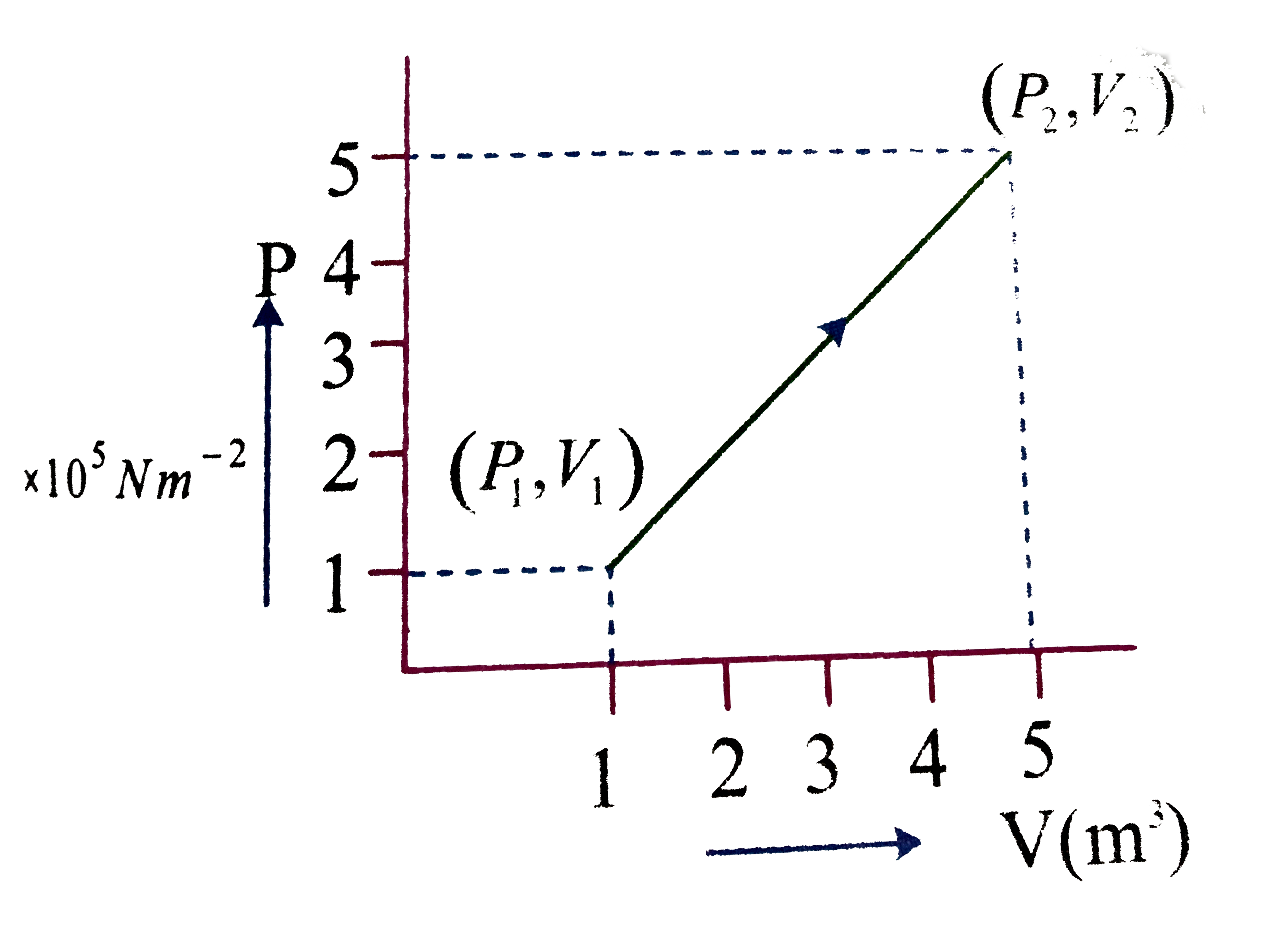
View SolutionA system changes from the state (P1,V1) to (P2,V2) as shown in the diagram. The work done by the system is
View SolutionOne mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View SolutionAn ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
View SolutionAssertion: When ideal gas expand from P1,V1,T1, to P2,V2,T2 two steps, and work done is high in which number of steps are high
Reason: Work is path function
View SolutionFor an ideal gas V−T curves at constant pressure P1 & P2 are shown in figure, from the figure
_E01_061_Q01.png)
View SolutionAn ideal gas expands adiabatically from an initial temperature T1 to a final temperature T2. Prove that the work done by the gas is CV(T1−T2).
View Solution
