The equation of two straight lines are x−12=y+31=z−2−3andx−21=y−1−3=z+32. Statement 1: the given lines are coplanar. Statement 2: The equations 2r−s=1,r+3s=4and3r+2s=5 are consistent.
Both the statements are true, and Statement 2 is the correct explanation for Statement 1.
Both the Statements are true, but Statement 2 is not the correct explanation for Statement 1.
Statement 1 is true and Statement 2 is false.
Statement 1 is false and Statement 2 is true.
The correct Answer is:d
Any point on the first line is (2x1+1,x1−3,−3x1+2).
Any point on the second line is (y1+2,−3y1+1,2y1−3).
If two lines are coplanar, then 2x1−y1=1,x1+3y1=4and3x1+2y1=5 are consistent.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE12videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
Similar Questions
The equation of two straight lines are x−12=y+31=z−2−3andx−21=y−1−3=z+32. Statement 1: the given lines are coplanar. Statement 2: The equations 2x1−y1=1,x1+3y1=4and3x−1+2y1=5 are consistent.
View SolutionThe equations of two straight lines are
x−12=y+31=z−2−3 and x−21=y−1−3=z+32
Statement 1: The given lines are coplanar.
Statement 2: The equations
2r−s=1
r+3s=4
3r+2s=5
are consistent.View SolutionGiven lines x−42=y+54=z−1−3andx−21=y+13=z2
Statement-I The lines intersect.
Statement-II They are not parallel.View SolutionShow that the lines x−13=y+12=z−15andx+24=y−13=z+1−2 do not intersect.
View SolutionShow that the lines x−13=y+12=z−15andx+24=y−13=z+1−2 do not intersect.
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFind the shortest distance between the lines x−12=y−23=z−34andx−23=y−44=z−55 .
View SolutionFor an ideal gas, an illustration of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
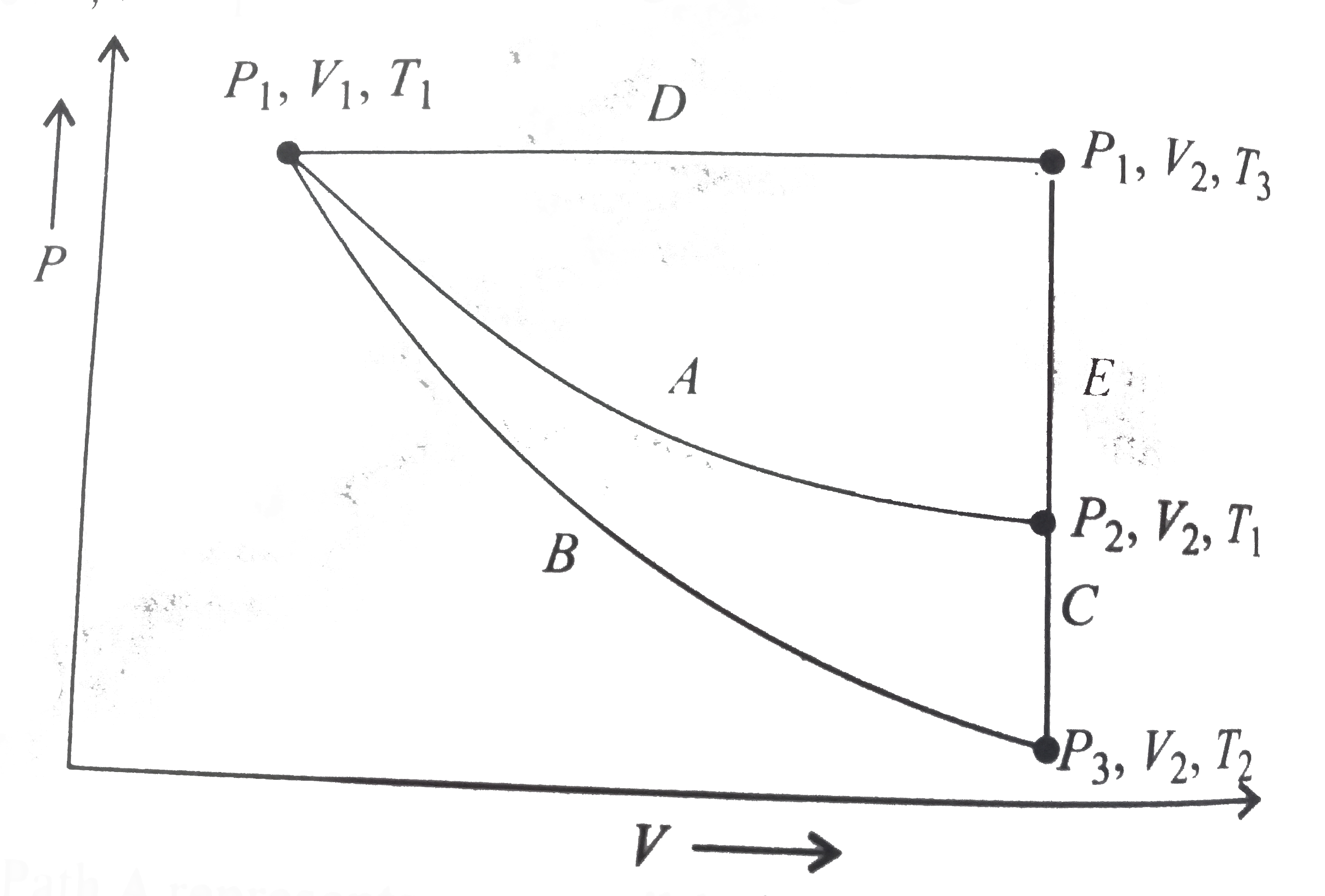
Path A represents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?View Solution


