Question

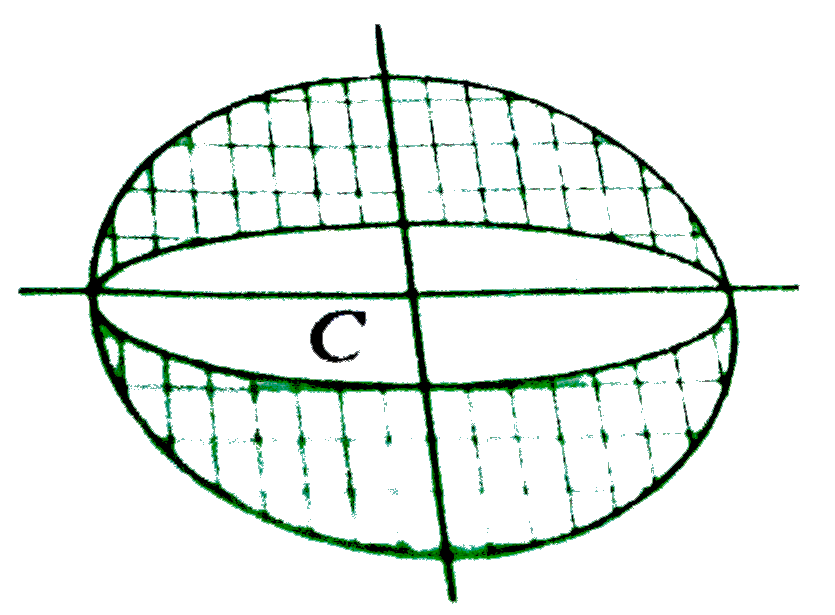
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity ${\displaystyle 2\sqrt{2}/3}$ is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
${\displaystyle 1-\frac{b^2}{a^2}=\frac{8}{9}\text{or}\frac{b^2}{a^2}=\frac{1}{9}}$
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
${\displaystyle p=\frac{\text{Area of shaded region}}{\text{Area of circle}}}$
${\displaystyle =\frac{\pi a^2-\pi ab}{\pi a^2}=1-\frac{b}{a}=1-\frac{1}{3}=\frac{2}{3}}$
Now, answer the following questions.

Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is

Options

A. `1//4`
B. `1//2`
C. `1//3`
D. `1//sqrt(2)`

Answer

A

Explanation

For the favorable cases, the points should lie inside the concentric circle of radius `r//2`. So the desired probability is given by

`("Area of smaller circle")/("Area of larger circle")=(.^(pi((r)/(2))^(2)))/(pir^(2)) = (1)/(4)`