A circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
The correct Answer is:1
To determine whether the statement "The point Q (6,8) lies outside the circle" is true or false, we will follow these steps:
Step 1: Identify the center and radius of the circle
The center of the circle is at the origin (0,0) and the point P (5,0) lies on the circle. The distance from the center to point P is the radius of the circle.
Calculation of radius:
- The radius r is the distance from the center (0,0) to the point P (5,0).
- Using the distance formula:
r=√(x2−x1)2+(y2−y1)2
where (x1,y1)=(0,0) and (x2,y2)=(5,0):
r=√(5−0)2+(0−0)2=√52=5
Step 2: Write the equation of the circle
The equation of a circle with center at (0,0) and radius r is given by:
x2+y2=r2
Substituting r=5:
x2+y2=52=25
Step 3: Determine the position of point Q (6,8)
Now we need to check if the point Q (6,8) lies inside, on, or outside the circle. We will substitute the coordinates of point Q into the circle's equation.
Calculation:
- Substitute x=6 and y=8 into the equation:
62+82=36+64=100
Step 4: Compare with the radius squared
Now we compare 100 with 25:
- Since 100>25, this means that the point Q (6,8) lies outside the circle.
Conclusion
Thus, the statement "The point Q (6,8) lies outside the circle" is True.
---
The center of the circle is at the origin (0,0) and the point P (5,0) lies on the circle. The distance from the center to point P is the radius of the circle.
- The radius r is the distance from the center (0,0) to the point P (5,0).
- Using the distance formula:
r=√(x2−x1)2+(y2−y1)2
where (x1,y1)=(0,0) and (x2,y2)=(5,0):
r=√(5−0)2+(0−0)2=√52=5
The equation of a circle with center at (0,0) and radius r is given by:
x2+y2=r2
Substituting r=5:
x2+y2=52=25
Now we need to check if the point Q (6,8) lies inside, on, or outside the circle. We will substitute the coordinates of point Q into the circle's equation.
- Substitute x=6 and y=8 into the equation:
62+82=36+64=100
Now we compare 100 with 25:
- Since 100>25, this means that the point Q (6,8) lies outside the circle.
Thus, the statement "The point Q (6,8) lies outside the circle" is True.
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 7.3 Very Short Answer Type Questions
Explore 20 Videos
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 7.4 Long Answer Type Questions
Explore 6 Videos
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 7.4 Long Answer Type Questions
Explore 6 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
- INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSBook:NCERT EXEMPLAR ENGLISHChapter:INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSExercise:LONG ANSWER TYPES QUESTIONS
Explore 18 Videos
Similar Questions
If |z|<1,then1+2z lies (A) on or inside circle having center at origin and radius 2 (B) outside the circle having center at origin and radius 2 (C) inside the circle having center at (1,0) and radius 2 (D) outside the circle having center at (1,0) and radius 2.
View SolutionA square is incribed in a circle . If p1 is the probability that a randomly chosen point of the circle lies within the square and p2 is the probability that the point lies outside the square then
View Solution
Knowledge Check
Circle C (not shown) is drawn on a coordinate plane, centered at the origins. If the point (a, b) lies on the circumference of the circle, what is the radius of the cirle in terms of a and b?
Aa−bBa+bC√a2+b2Da2+b2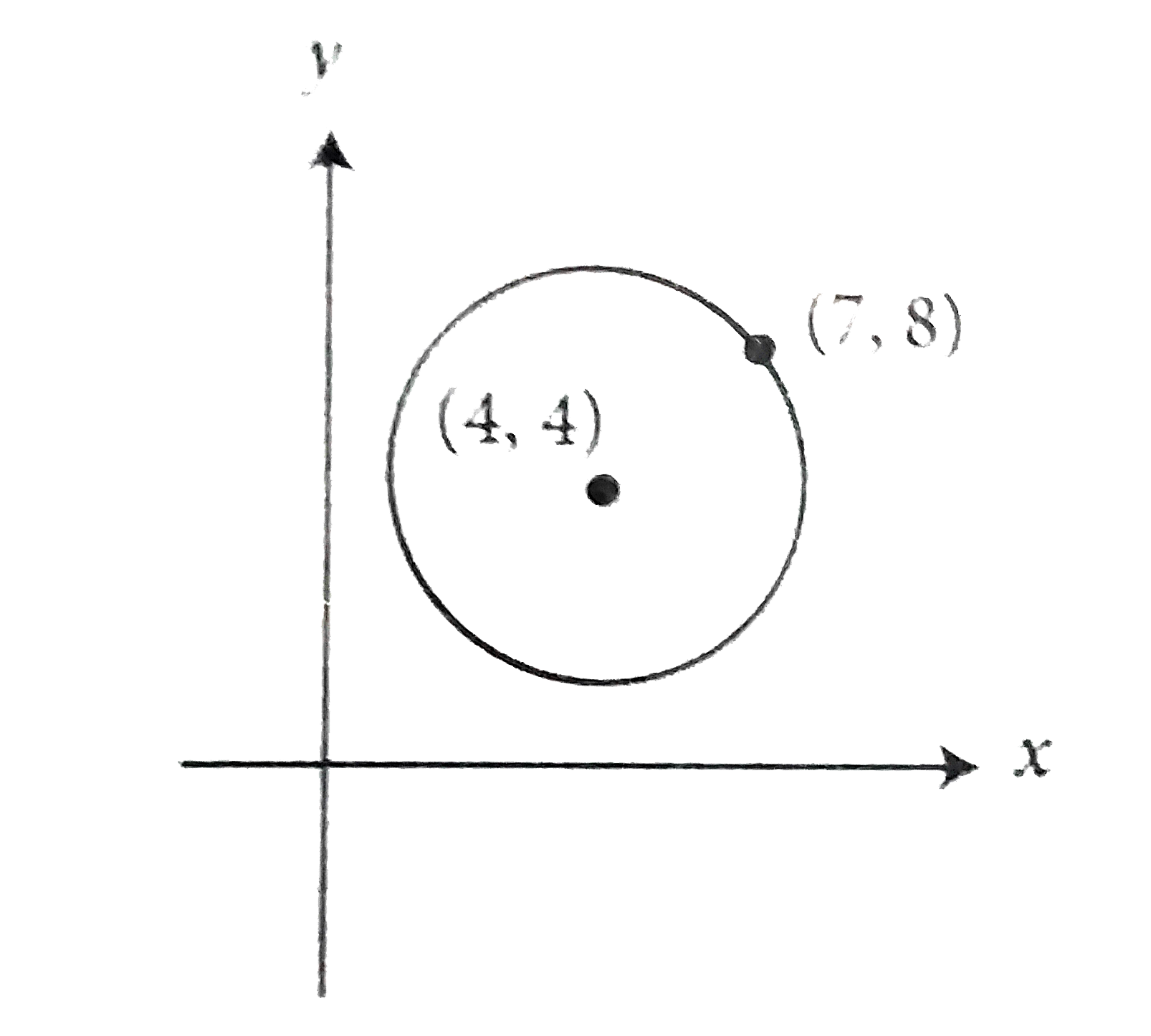
the circle defined by the equation (x−4)2+(y−4)2=25 has its centre at point (4,4) and includes point (7,8) on the circle. This is shown in the figure above. What is the area of the circle shown?A5πB10πC16πD25π
A circle of maximum area is inscribed in an ellipse. If p is the probability that a point within the ellipse chosen at random lies outside the circle, then the eccentricity of the ellipse is
View SolutionMake a point A. Taking A as centre draw two circles, one with radius 5 cm and the other with radius 7 cm. Draw line segments AB and AC where AB is a radius of the smaller circle and AC a radius of the bigger circle. Mark points P, Q, R such that point P is inside both the circles, Q is outside the smaller circle but inside the bigger one and point R is outside both the circles.
View SolutionThe line 2x−y+1=0 touches a circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The diameter (in units) of the circle is
View SolutionIf the point (x,4) lies on a circle whose centre is at the origin and radius is 5, then x= ±5 (b) ±3 (c) 0 (d) 14
View SolutionDraw a circle with centre O and radius 6 cm . Mark points P, Q, R such that P lies on the circle, Q lies in the interior of the circle , and R lies in the exterior of the circle. Rewrite each of the following statements using the correct symbol (=, ⟨or⟩): (i) OQ5 cm (ii) OP.5cm (iii) OR.5 cm
View SolutionA circle of radius 2 has its centre at (2, 0) and another circle of radius 1 has its centre at (5, 0). A line is tangent to the two circles at point in the first quadrant. The y-intercept of the tangent line is
View Solution

