A double-decker bus carry passengers, in the upper deck and in the lower deck. Find the number of ways in which the passengers can be distributed in the two decks, if particular passengers refuse to go in the upper deck and refuse to sit in the lower deck.
To solve the problem of distributing passengers in a double-decker bus, we can break it down into a series of logical steps.
1. Understanding the Problem:
- We have a total of u+l passengers.
- u passengers can sit in the upper deck.
- l passengers can sit in the lower deck.
- There are r passengers who refuse to sit in the upper deck.
- There are s passengers who refuse to sit in the lower deck.
2. Identifying Fixed Passengers:
- The r passengers who refuse to go to the upper deck must sit in the lower deck. Therefore, they occupy r seats in the lower deck.
- The s passengers who refuse to sit in the lower deck must sit in the upper deck. Therefore, they occupy s seats in the upper deck.
3. Calculating Remaining Passengers:
- After placing the r and s passengers, the remaining passengers are:
(u+l)−(r+s)=u+l−r−s
- These remaining passengers can be distributed in the upper and lower decks.
4. Calculating Available Seats:
- The number of available seats in the lower deck after placing r passengers is:
l−r
- The number of available seats in the upper deck after placing s passengers is:
u−s
5. Distributing Remaining Passengers:
- We need to distribute the remaining u+l−r−s passengers into the remaining seats in both decks.
- The number of ways to choose which of the remaining passengers will sit in the lower deck is given by the combination formula:
(u+l−r−sl−r)
- This represents choosing l−r passengers from the total remaining passengers to sit in the lower deck.
6. Final Expression:
- The total number of ways to distribute the passengers is:
Total Ways=(u+l−r−sl−r)
Final Answer:
The number of ways in which the u+l passengers can be distributed in the two decks is:
(u+l−r−sl−r)
- We have a total of u+l passengers.
- u passengers can sit in the upper deck.
- l passengers can sit in the lower deck.
- There are r passengers who refuse to sit in the upper deck.
- There are s passengers who refuse to sit in the lower deck.
- The r passengers who refuse to go to the upper deck must sit in the lower deck. Therefore, they occupy r seats in the lower deck.
- The s passengers who refuse to sit in the lower deck must sit in the upper deck. Therefore, they occupy s seats in the upper deck.
- After placing the r and s passengers, the remaining passengers are:
(u+l)−(r+s)=u+l−r−s
- These remaining passengers can be distributed in the upper and lower decks.
- The number of available seats in the lower deck after placing r passengers is:
l−r
- The number of available seats in the upper deck after placing s passengers is:
u−s
- We need to distribute the remaining u+l−r−s passengers into the remaining seats in both decks.
- The number of ways to choose which of the remaining passengers will sit in the lower deck is given by the combination formula:
(u+l−r−sl−r)
- This represents choosing l−r passengers from the total remaining passengers to sit in the lower deck.
- The total number of ways to distribute the passengers is:
Total Ways=(u+l−r−sl−r)
The number of ways in which the u+l passengers can be distributed in the two decks is:
(u+l−r−sl−r)
Topper's Solved these Questions
Similar Questions
A double-decker bus carry (u+e) passengers, u in the upper deck and e in the lower deck. Find the number of ways in which the u+e passengers can be distributed in the two decks, if r(≤e) particular passengers refuse to go in the upper deck and s(≤u) refuse to sit in the lower deck.
View SolutionPassengers are to travel by a double decked bus which can accommodate 13 in the upper deck and 7 in the lower deck. Find the number of ways that they can be distributed if 5 refuse to sit in the upper deck and 8 refuse to sit in the lower deck.
View SolutionA double -decker bus has 5 empty seats in the upper deck and 5 empty seats in the lower deck. 10 people board the bus of which 2 are old people and 3 are children. The children refuse to take seats lower deck while old people insist to stay lower deck. How many different sitting arrangements of the people are possible ?
View SolutionNumber of ways in which the letters of the word ‘B U L B U L’ can be arranged in a line in any order is also equal to the:
View SolutionLe Chatelier's Principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way as to nullify the effect of that change.
Change of pressure : If a system consists of gases, then the concentration of all the components can be alterd by changing the pressure. To increase the pressure on the system,the volume has to be decreased proportionally. The total number of mols per unit volume will now be more and the equilibrium will shift in the direction in which there is a decrease in number of moles i,e. towards the direction in which there can be decrease in pressure.
Effect of pressure on melting point : There are two types of solids:
(a) Solids whose volume decreases on melting e.g., ice,diamond carborundum magnesium nitride and quratz.
Solids (higher volume)⇔Liquid (lower volume) The process of melting is facilitated at high pressure, thus, melting point is lowerd.
(b) Solids whose volume increase on melting e.g.,Fe,Cu,Ag,Au,etc.
Solid (lower volume)⇔ Liquid (higher volume) In this case the process of melting become difficult at high pressure, thus melting point becomes high.
(c) Solubility of substances : When solid substances are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCI+aq⇔KCI(aq)−heat
In such cases, solubility increase with increase in temperature. Consider the case of KOH, when this is dissolved,heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d) Solubility of gases in liquids : When a gas dissolves in liquid,there is decrease in volume. Thus increase of pressure will favour the dissolution of gas in liquid.
Au(s)⇔Au(l)
Above equsilibrium is favoured at :
View SolutionA heavy block B is sliding with constant velocity u=5m/s on a horizontal table. The width of the block is L=4m.
There is an insect A at distance d=3m from the block as shown in the figure. The insect wants to cross to the oposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v (in m/s) for which the insect can cross to the other side without getting hit by the block.

View SolutionTwo identical unifrom rods OA and OB each of length l and mass m are connected to each other by a massless pin connection (both the rods can rotate about O which is free to move), that allows free rotation. The assembly is kept on a frictionless horizontal plane. Now two point masses each of mass m moving with speed u perpendicular to the AB and hit the assembly inelastically at points A and B as shown in the figure.
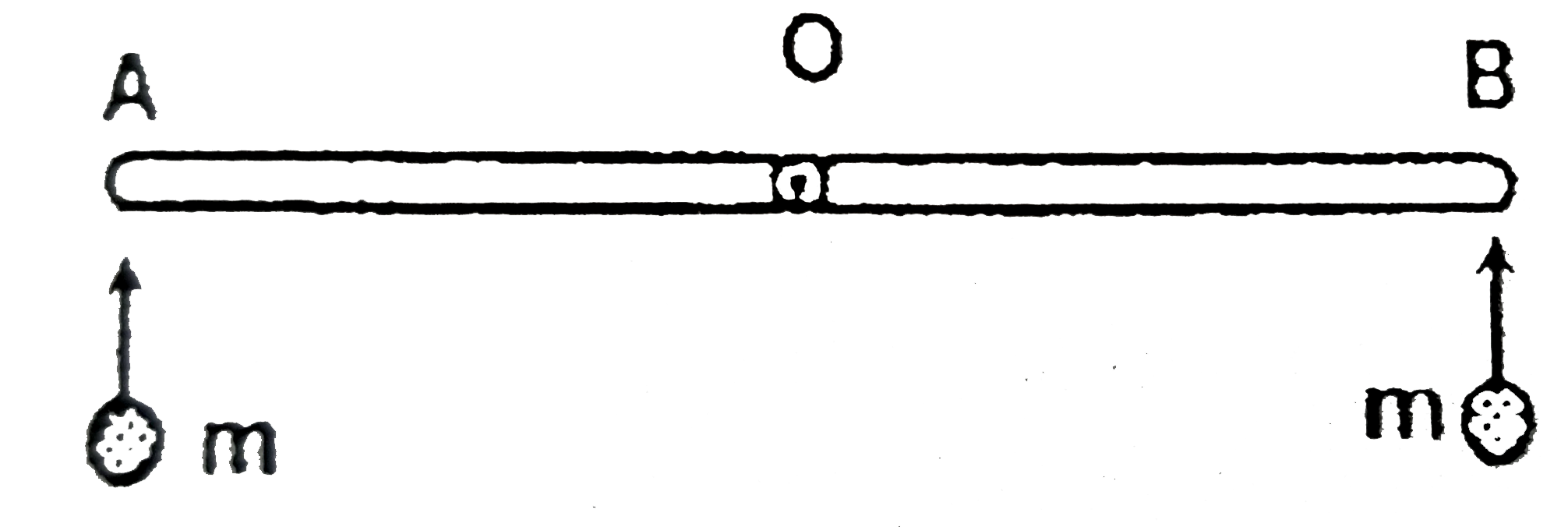
Find the angular speed of rods just after the collision
View SolutionTwo identical unifrom rods OA and OB each of length l and mass m are connected to each other by a massless pin connection (both the rods can rotate about O which is free to move), that allows free rotation. The assembly is kept on a frictionless horizontal plane. Now two point masses each of mass m moving with speed u perpendicular to the AB and hit the assembly inelastically at points A and B as shown in the figure.

Find the speed of centre of rod AO just after the collision.
View SolutionTwo long concetric cylindrical conductors of radii a and b (b<a) are maintained at a potential difference V and carry equal and opposite currents l. Show that an electron with a particular velocity u parallel to the axis may travel underivated in the evacuated region between the conductors, and calculate u when a = 50 mm, b = 2.0 mm, V = 50 V and l = 100 A.
It is also possible for the electron to travel in a helical path. By regarding such a path as the combination of a circular motion perpendicular to the axis with a steady velocity parallel to the axis, indicate without detailed mathematics how this comes about.
View SolutionShows a wire of length l which can slide on a U- shaped rail of negligible resistance. The resistance of the wire is R. The wire is pulled ot the right with a constant speed v. Draw an equivalent circuit diagram representing the induced emf by a battery. Find the current in the wire usingj this diagram.
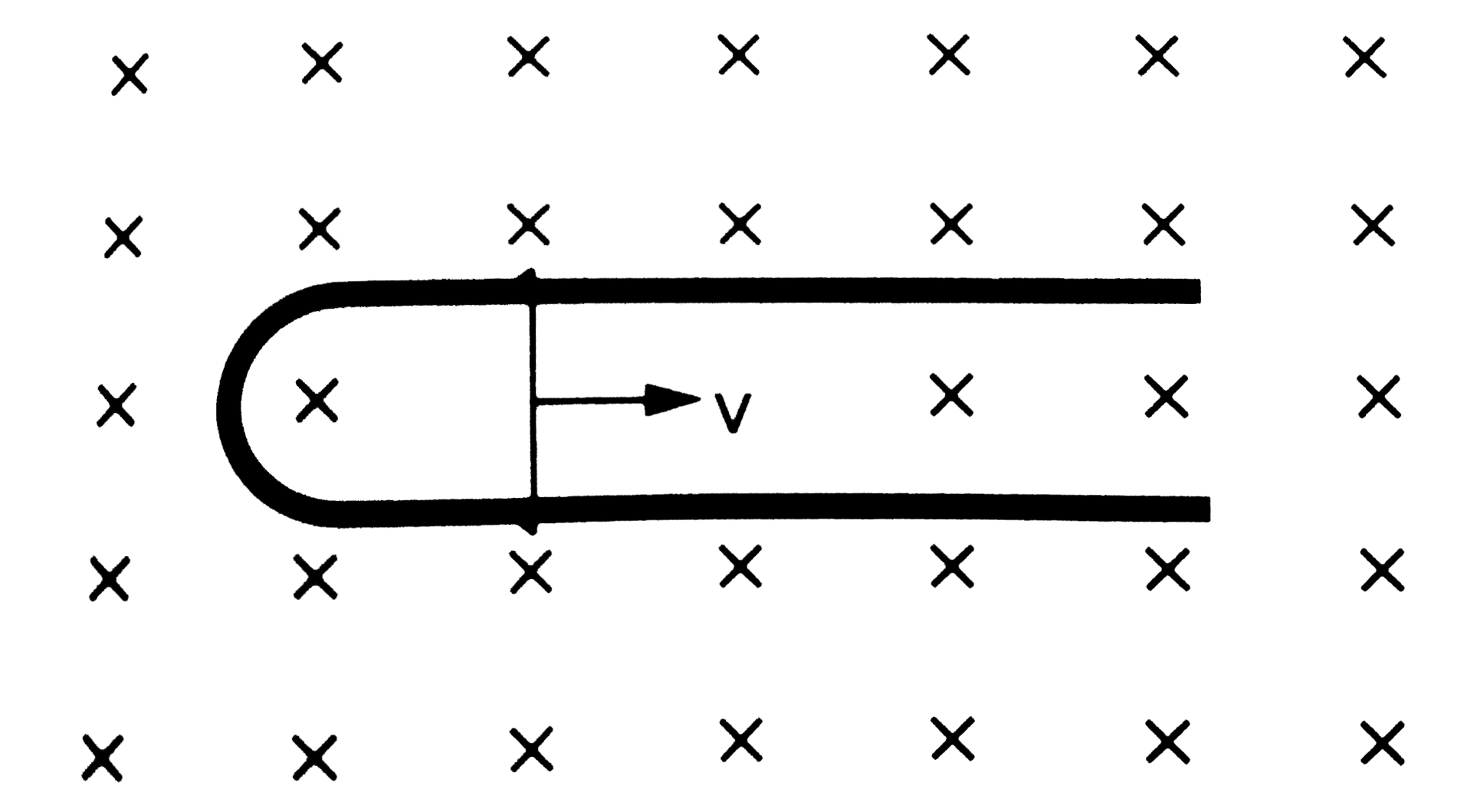

View Solution

