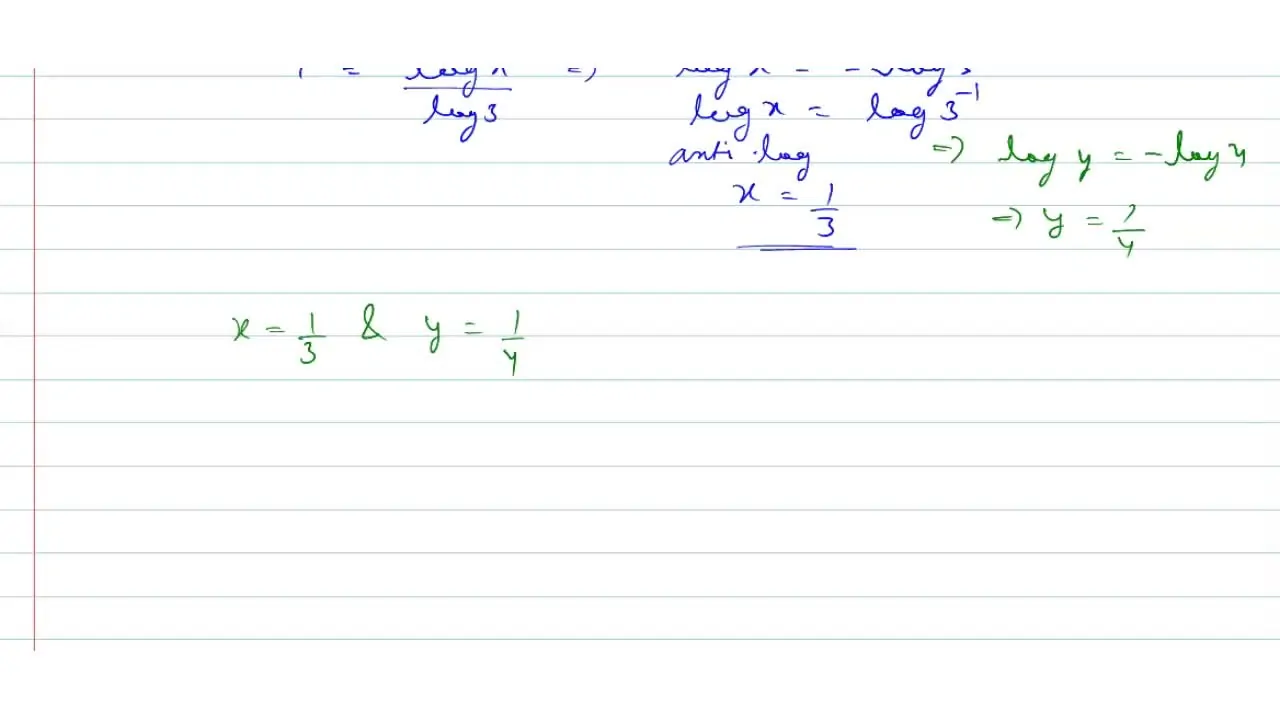Solve the equations for xandy:(3x)log3=(4y)log4,4logx=3logy.
Step by step video & image solution for Solve the equations for x and y:(3x)^(log3)=(4y)^(log 4), 4 ^(log x) = 3 ^(log y). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
Solve the equation for x:log4+(1+12x)log3=log(31x+27)
View SolutionSolve the equation 2xlog34+3logx4=27
View SolutionSolve for x :
3^(log x)-2^(log x) =2^(log x+1)-3^(log x-1)View SolutionSolve the following equations for x and y: log10x+log10(x)12+log10(x)14+….=y 1+3+5+…+(2y−1)4+7+10+..+(3y+1)=207log10x
View SolutionSolve the following equations.
(iii) 2.xlog43+3log4x=27View SolutionSolve the derivative of y=log2x3
View SolutionSolve the differential equation xdydx=y(logy−logx+1).
View SolutionSolve the system of equations: (log)ax(log)a(xyz)=48(log)ayloga(xyz)=12, a>0, a≠1(log)azloga(xyz)=84
View SolutionSolve the following equation for x & y:(log)100|x+y|=12,(log)10|x|=log1004.
View SolutionSolve the following equation of x:2(log)xa+(log)axa+3(log)a2xa=0,a>0
View Solution