One half of a convex lens of focal length 10 cm is covered with a black paper. Can such
a lens produce an image of a complete object placed at a distance of 30 cm from the
lens? Draw a ray diagram to justify your answer. A 4 can tall object is placed
perpendicular to the perpendicular to the principal axis of a convex lens of focal length 20 cm. The distince
of the object from the less is 15 cm. Find nature, position and size of the image.
Step-by-Step Solution
1. Identify Given Data:
- Focal length of the lens (f) = 10 cm
- Object distance (u) = -30 cm (negative as per sign convention)
2. Use the Lens Formula:
The lens formula is given by:
1f=1v−1u
Rearranging gives:
1v=1f+1u
3. Substitute the Values:
1v=110+1−30
Finding a common denominator (30):
1v=330−130=230=115
Thus,
v=15 cm
4. Determine the Nature of the Image:
- Since the object is beyond the 2F point (which is at 20 cm for this lens), the image formed is real, inverted, and diminished.
5. Effect of Half Lens Covered:
- Although the image is formed at 15 cm, the intensity of the image will be reduced because only half of the lens is functioning. The image will still be formed, but it will be dimmer.
6. Ray Diagram:
- Draw a ray diagram showing the convex lens, the object on the left, and the image on the right at 15 cm. Indicate the rays converging to form the image.
Part 2: Image Formation for a 4 cm Tall Object
1. Identify Given Data:
- Focal length of the lens (f) = 20 cm
- Object distance (u) = -15 cm
- Height of the object (h_o) = 4 cm
2. Use the Lens Formula:
1f=1v−1u
Rearranging gives:
1v=1f+1u
3. Substitute the Values:
1v=120+1−15
Finding a common denominator (60):
1v=360−460=−160
Thus,
v=−60 cm
4. Determine the Nature of the Image:
- The negative sign indicates that the image is virtual and located on the same side as the object. The image is upright and larger than the object.
5. Calculate the Size of the Image:
Using the magnification formula:
Magnification (m)=hiho=−vu
Substituting the values:
m=−−60−15=4
Thus,
hi=m⋅ho=4⋅4 cm=16 cm
6. Ray Diagram:
- Draw a ray diagram showing the convex lens, the object on the left, and the virtual image on the same side at 60 cm, indicating the rays diverging.
Summary of Results:
- For the first part, the image is formed at 15 cm, real, inverted, and diminished.
- For the second part, the image is virtual, upright, and 16 cm tall.
- Focal length of the lens (f) = 10 cm
- Object distance (u) = -30 cm (negative as per sign convention)
The lens formula is given by:
1f=1v−1u
Rearranging gives:
1v=1f+1u
1v=110+1−30
Finding a common denominator (30):
1v=330−130=230=115
Thus,
v=15 cm
- Since the object is beyond the 2F point (which is at 20 cm for this lens), the image formed is real, inverted, and diminished.
- Although the image is formed at 15 cm, the intensity of the image will be reduced because only half of the lens is functioning. The image will still be formed, but it will be dimmer.
- Draw a ray diagram showing the convex lens, the object on the left, and the image on the right at 15 cm. Indicate the rays converging to form the image.
- Focal length of the lens (f) = 20 cm
- Object distance (u) = -15 cm
- Height of the object (h_o) = 4 cm
1f=1v−1u
Rearranging gives:
1v=1f+1u
1v=120+1−15
Finding a common denominator (60):
1v=360−460=−160
Thus,
v=−60 cm
- The negative sign indicates that the image is virtual and located on the same side as the object. The image is upright and larger than the object.
Using the magnification formula:
Magnification (m)=hiho=−vu
Substituting the values:
m=−−60−15=4
Thus,
hi=m⋅ho=4⋅4 cm=16 cm
- Draw a ray diagram showing the convex lens, the object on the left, and the virtual image on the same side at 60 cm, indicating the rays diverging.
- For the first part, the image is formed at 15 cm, real, inverted, and diminished.
- For the second part, the image is virtual, upright, and 16 cm tall.
Similar Questions
A 2.0cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 10 cm. The distance of the object from the lens is 15 cm. Find the nature, position and size of the image. Also, find its magnification.
View SolutionA 1.5 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 15 cm. Distance of object from the lens is 20 cm. Use lens formula to find the nature, position and size of the image.
View SolutionAn object of height 2 cm is placed in front of a convex lens of focal length 20 cm at a distance of 15 cm from it. Find the position and magnification of the image.
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
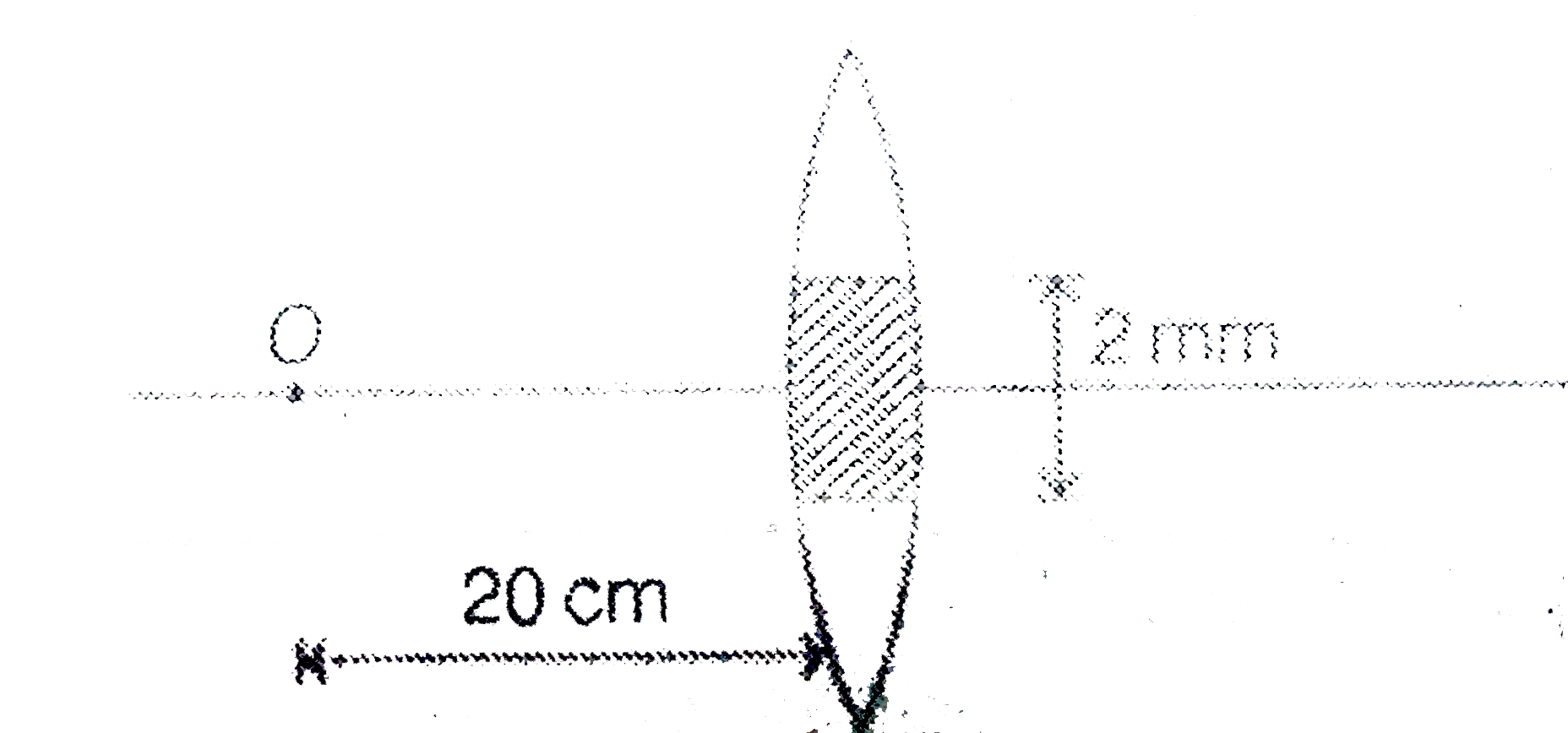
View SolutionAn object of length 2.0 cm is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. Find the size of the image of the object is at a distance of 8.0 cm from the lens.
View SolutionA thin linear object of size 1mm is kept along the principal axis of a convex lens of focal length 10cm. The object is at 15cm from the lens. The length of the image is:
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn extended real object of size 2cm is palced perpendicular to the principle axis of a converging lens of focal length 20cm. The distance between the object and the lens is 30cm
(i) Find the laterial magnification produced by the lens.
(ii) Find the height of the image.
View SolutionOne half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object? Verify your answer experimentally. Explain your observations.
View SolutionA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View Solution