Combinations and Comparison of Capacitors and Resistors
To solve the problem of combinations and comparison of capacitors and resistors, we will break it down into steps for both series and parallel combinations for resistors and capacitors.
Step 1: Series Combination of Resistors
1. Identify the Resistors: Let’s denote the resistors as R1,R2,R3,…,Rn.
2. Connect in Series: In a series combination, the resistors are connected end-to-end.
3. Calculate Equivalent Resistance: The total or equivalent resistance RAB between points A and B is given by:
RAB=R1+R2+R3+…+Rn
Step 2: Parallel Combination of Resistors
1. Identify the Resistors: Again denote the resistors as R1,R2,R3,…,Rn.
2. Connect in Parallel: In a parallel combination, the resistors are connected across the same voltage source.
3. Calculate Equivalent Resistance: The total or equivalent resistance RAB is given by:
1RAB=1R1+1R2+1R3+…+1Rn
Step 3: Series Combination of Capacitors
1. Identify the Capacitors: Let’s denote the capacitors as C1,C2,C3,…,Cn.
2. Connect in Series: In a series combination, the capacitors are connected end-to-end.
3. Calculate Equivalent Capacitance: The total or equivalent capacitance CAB between points A and B is given by:
1CAB=1C1+1C2+1C3+…+1Cn
Step 4: Parallel Combination of Capacitors
1. Identify the Capacitors: Again denote the capacitors as C1,C2,C3,…,Cn.
2. Connect in Parallel: In a parallel combination, the capacitors are connected across the same voltage source.
3. Calculate Equivalent Capacitance: The total or equivalent capacitance CAB is given by:
CAB=C1+C2+C3+…+Cn
Summary of Results:
- Resistors in Series: RAB=R1+R2+R3+…+Rn
- Resistors in Parallel: 1RAB=1R1+1R2+1R3+…+1Rn
- Capacitors in Series: 1CAB=1C1+1C2+1C3+…+1Cn
- Capacitors in Parallel: CAB=C1+C2+C3+…+Cn
1. Identify the Resistors: Let’s denote the resistors as R1,R2,R3,…,Rn.
2. Connect in Series: In a series combination, the resistors are connected end-to-end.
3. Calculate Equivalent Resistance: The total or equivalent resistance RAB between points A and B is given by:
RAB=R1+R2+R3+…+Rn
1. Identify the Resistors: Again denote the resistors as R1,R2,R3,…,Rn.
2. Connect in Parallel: In a parallel combination, the resistors are connected across the same voltage source.
3. Calculate Equivalent Resistance: The total or equivalent resistance RAB is given by:
1RAB=1R1+1R2+1R3+…+1Rn
1. Identify the Capacitors: Let’s denote the capacitors as C1,C2,C3,…,Cn.
2. Connect in Series: In a series combination, the capacitors are connected end-to-end.
3. Calculate Equivalent Capacitance: The total or equivalent capacitance CAB between points A and B is given by:
1CAB=1C1+1C2+1C3+…+1Cn
1. Identify the Capacitors: Again denote the capacitors as C1,C2,C3,…,Cn.
2. Connect in Parallel: In a parallel combination, the capacitors are connected across the same voltage source.
3. Calculate Equivalent Capacitance: The total or equivalent capacitance CAB is given by:
CAB=C1+C2+C3+…+Cn
- Resistors in Series: RAB=R1+R2+R3+…+Rn
- Resistors in Parallel: 1RAB=1R1+1R2+1R3+…+1Rn
- Capacitors in Series: 1CAB=1C1+1C2+1C3+…+1Cn
- Capacitors in Parallel: CAB=C1+C2+C3+…+Cn
Topper's Solved these Questions
Similar Questions
Combination of two identical capacitors, a resistor R and a dc voltage source of voltage 6V is used in an experiment on a (C−R) circuit. It is found that for a parallel combination of the capacitor the time in which the voltage of the fully charged combinatiomn reduces to half its original voltage is 10 second. For series combination the time needed for reducing teh voltage of the fully charged series combination by half is-
View SolutionFigure shows a part of network of a capacitor and resistors. The potential indicated at A, B and C are with respect to the ground. The charge on the capacitor on the capacitor in steady state is
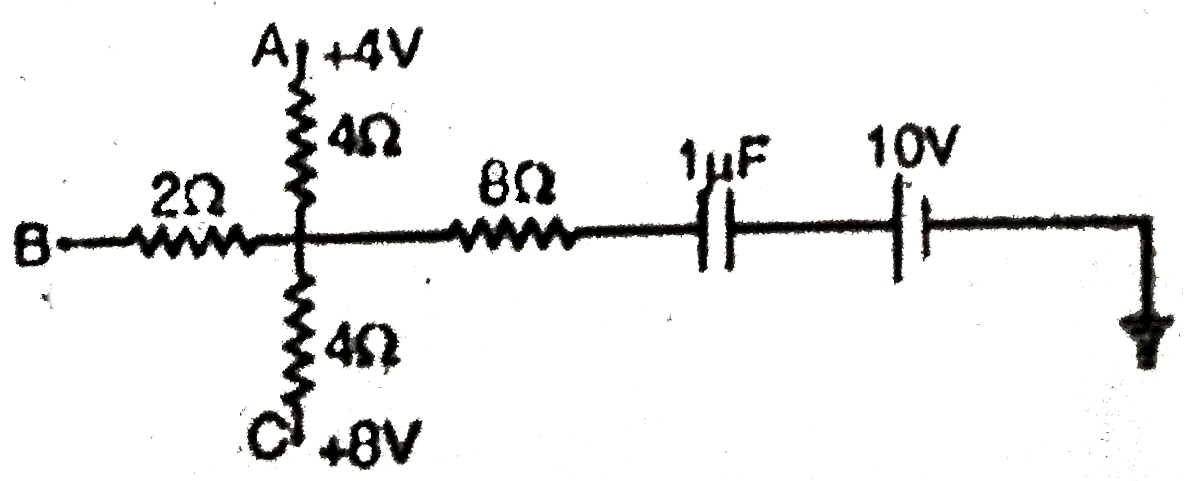
View Solution
Knowledge Check
Assertion- In a series combination of capacitors, charge on each capacitor is same.
Reason- In such a combination, charge cannot move only along one route.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
The V-I graph for a series combination and for a parallel combination of two resistor is shown in the figure below. Which of the two A or B, represents the parallel combination? Give a reason for your answer.
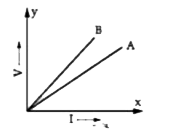
View SolutionThe V-I graph for a series combination and for a parallel combination of two resistors is 1 shown in Fig. Which of the V two, A or B, represents the parallel combination ? Give a reason for your answer.
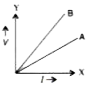
View SolutionThe V-I graph for a series combination and for a parallel combination of two resistor is shown in the figure below. Which of the two A or B, represents the parallel combination? Give a reason for your answer.
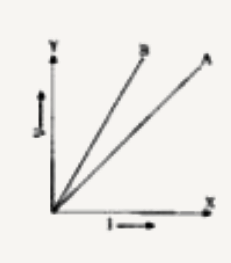
View SolutionFigure shows a network of a capacitor and resistors. Find the charge on capacitor in steady state in μC.
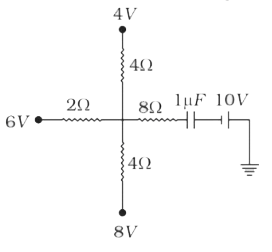
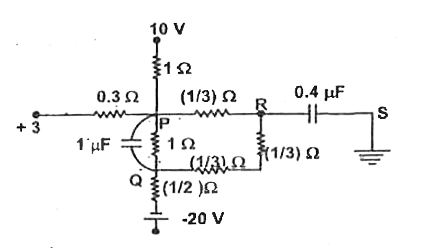
View SolutionShown in the figure is network of capacitors & resistors. The potentials of some of the nodes are given. Find the
(a) potential of
(b) energy stored in the capacitor connected between R&S
(c) energy stored in the capacitor connected between P&Q
View SolutionIf capacitor with capacitance C,2C are initially at potential v, 2v resp. Now they are connected in parallel combination such that end of charge of (∩aci→r)1 & -ve charge of (∩aci→r)2 are on same side. Find energy loss
View Solutionfigure, shows a source of alternating voltage connected to a capacitor and a resistor. Which of the following phasor diagrams correctly describes the phase relationshop between (IC) the current between the source and the capacitor and (IR) the current between the source and the resistor?

View Solution

