Ram was a daily wage worker in a factory. He was suffering from Cancer. On hearing this, most of his co-workers, started avoiding him under the impression that it was a contagious disease. When Prof. Srivastava came to know about this, case, he took him to a leading radiologist, who examined him and told that it was at the beginning stage. He advised that it could be easily cured and also certified that it was not a communicable disease. After this, Ram was given proper treatment by the doctor and got cured completely.
(1) How is mean life of a radioactive element related to its half life?
(2) A radioactive sample has activity of 10,000 disintegrations per second after 20 hours . After next 10 hours, its activity reduces to 5,000 dps. Find out its half - life and initial activity.
Step-by-Step Solution
1. The mean life (τ) is defined as the average time a particle exists before decaying:
τ=1λ
where λ is the decay constant.
2. The half-life (t₁/₂) is the time taken for half of the radioactive substance to decay:
t1/2=ln(2)λ
3. To express the half-life in terms of mean life, we can rearrange the equations:
t1/2=ln(2)⋅τ
Thus, the relationship between mean life and half-life is:
t1/2=ln(2)⋅τ
---
(2) Finding Half-Life and Initial Activity
Given:
- Activity after 20 hours (A₁) = 10,000 disintegrations per second (dps)
- Activity after 30 hours (A₂) = 5,000 dps
We know that the activity of a radioactive sample can be expressed as:
A=A0e−λt
Where:
- A0 = initial activity
- λ = decay constant
- t = time elapsed
Step 1: Set up the equations for both time points.
For the first time point (20 hours):
10,000=A0e−λ⋅20(Equation 1)
For the second time point (30 hours):
5,000=A0e−λ⋅30(Equation 2)
Step 2: Divide Equation 1 by Equation 2.
10,0005,000=A0e−λ⋅20A0e−λ⋅30
This simplifies to:
2=e−λ⋅20⋅eλ⋅30
This can be rewritten as:
2=eλ⋅10
Step 3: Take the natural logarithm of both sides.
ln(2)=λ⋅10
Thus, we can express the decay constant:
λ=ln(2)10
Step 4: Substitute λ back to find A₀.
Using Equation 1:
10,000=A0e−(ln(2)10)⋅20
This simplifies to:
10,000=A0e−2ln(2)=A0⋅14
Thus:
A0=10,000⋅4=40,000 dps
Step 5: Find the half-life (t₁/₂).
Using the relationship:
t1/2=ln(2)λ
Substituting λ:
t1/2=ln(2)ln(2)10=10 hours
Final Answers:
1. The relationship between mean life and half-life is given by:
t1/2=ln(2)⋅τ
2. The half-life (t₁/₂) is 10 hours and the initial activity (A₀) is 40,000 dps.
---
τ=1λ
where λ is the decay constant.
t1/2=ln(2)λ
t1/2=ln(2)⋅τ
t1/2=ln(2)⋅τ
- Activity after 20 hours (A₁) = 10,000 disintegrations per second (dps)
- Activity after 30 hours (A₂) = 5,000 dps
A=A0e−λt
- A0 = initial activity
- λ = decay constant
- t = time elapsed
10,000=A0e−λ⋅20(Equation 1)
5,000=A0e−λ⋅30(Equation 2)
2=e−λ⋅20⋅eλ⋅30
2=eλ⋅10
λ=ln(2)10
10,000=A0e−(ln(2)10)⋅20
10,000=A0e−2ln(2)=A0⋅14
A0=10,000⋅4=40,000 dps
t1/2=ln(2)λ
t1/2=ln(2)ln(2)10=10 hours
1. The relationship between mean life and half-life is given by:
t1/2=ln(2)⋅τ
2. The half-life (t₁/₂) is 10 hours and the initial activity (A₀) is 40,000 dps.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-I (SECTION-A)
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-I (SECTION-B)
Explore 5 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section-E
Explore 17 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
Does the charge given to a metallic sphere depend on whether it is hollow or solid ? Give reason for your answer.
View SolutionHow does Ampere-Maxwell law explain the flow the of current through a capacitor when it is being charged by a battery? Write the expression for the displacement current in terms of the rate of change of electric flux.
View SolutionHow much current is drawn by the primary of a transformer connected to 220V supply when it delivers power to a 110V−550W refrigerator ?
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
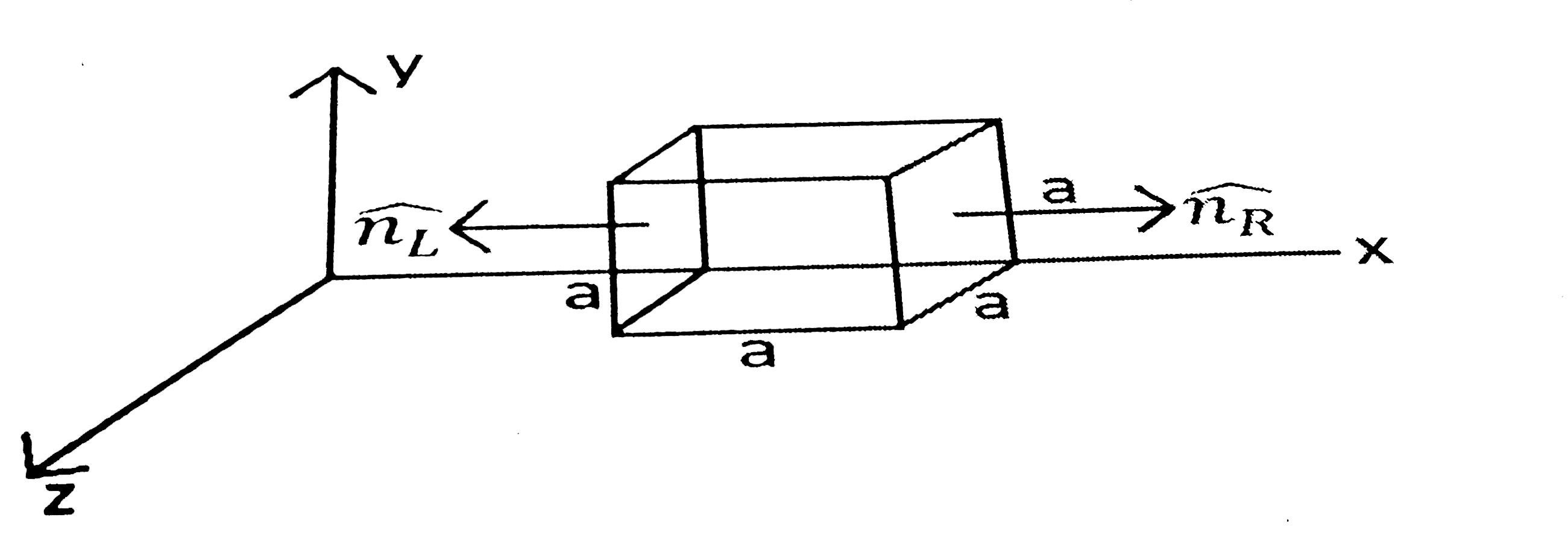
View SolutionRam was a daily wage worker in a factory. He was suffering from Cancer. On hearing this, most of his co-workers, started avoiding him under the impression that it was a contagious disease. When Prof. Srivastava came to know about this, case, he took him to a leading radiologist, who examined him and told that it was at the beginning stage. He advised that it could be easily cured and also certified that it was not a communicable disease. After this, Ram was given proper treatment by the doctor and got cured completely. (1) What moral values did Prof. Srivastava display ? (2) How is mean life of a radioactive element related to its half life? (3) A radioactive sample has activity of 10,000 disintegrations per second after 20 hours . After next 10 hours, its activity reduces to 5,000 dps. Find out its half - life and initial activity.
View SolutionWorkers of a factory are always going to production manager for guidance and information. As a result, he is overburdened with work. Suggest him as to what he can do to relieve himself?
View Solutionकिसी फैक्टरी के श्रमिकों की दैनिक मजदूरी के निम्नलिखित बंटन पर विचार कीजिए :
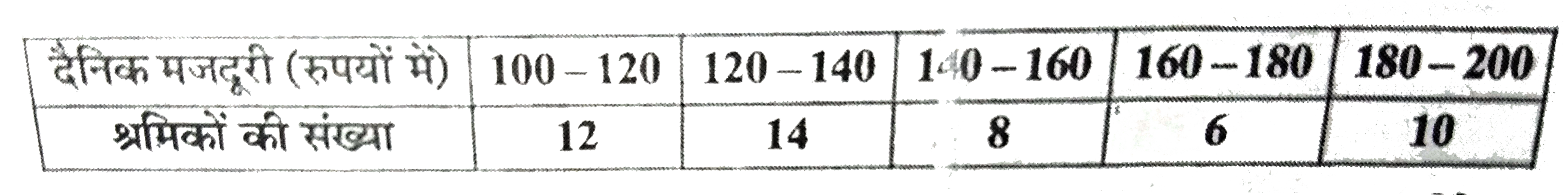
एक उपयुक्त विधि का प्रयोग करते हुए, इस फ़ैक्ट्री के श्रमिक की माध्य दैनिक मजदूरी ज्ञात कीजिए।
View Solutionकिसी फैक्टरी के 50 श्रमिकों की दैनिक मजदूरी के निम्नलिखित बंटन पर विचार कीजिएः

इस फैक्टरी के श्रमिकों की माध्य दैनिक मजदूरी ज्ञात कीजिए |
View SolutionHe hid _______ his pursuers could not find him.
View SolutionSwami Vivekanand once speaking in America told about a young man who came to a religious conference and said nothing. The young man returned time after time, ever repeating his desire, his longing to find God. After many days, the sage told him to accompany him as he went to the river to take his morning bath and when both were in the river, the sage took hold of the young man and plunged him under the surface of water and held him there. The young man struggled to shake off his hold. Finally he raised him out of water and asked him : "My son, what did you long for most when under water" ? "A breath of air", gasped the young. "Thus should a disciple long after God if he would find him. If you have this longing after God, verily, He should be found by you." said the sage.
The youngman struggled to........
View SolutionThe table representing the daily wages of workers ina factory is given below:- Find the mean of daily wages of workers. .
View SolutionIf a person can see an object clearly when it is placed at about 25 cm away from him, he is suffering from
View SolutionEverybody who know him agree that he rarely loses his temper.
View SolutionThe official found himself _________ when he could not explain his actions and all the members started attacking him with accusations of cheating.
View SolutionThe moment the manager came to know of the fraudulent action of his assistant, he order immediately dismissed him.
View Solution

