For an ideal inductor, connected across a sinusoidal ac voltage source, state which one of the following quantity is zero:
(i) Instantaneous power is zero :
(ii) Average power over full cycle of the ac voltage source.
To solve the question regarding the instantaneous power and average power in an ideal inductor connected to a sinusoidal AC voltage source, we will follow these steps:
1. Understand the Circuit:
- We have an ideal inductor (L) connected to a sinusoidal AC voltage source, which can be represented as e(t)=E0sin(ωt).
2. Determine the Current:
- In an inductive circuit, the current lags the voltage by a phase difference of π2 radians. Therefore, the current can be expressed as:
i(t)=I0sin(ωt−π2)=I0cos(ωt)
3. Calculate Instantaneous Power:
- The instantaneous power p(t) is given by the product of voltage and current:
p(t)=e(t)⋅i(t)=E0sin(ωt)⋅I0cos(ωt)
- Using the identity sin(x)cos(x)=12sin(2x), we can rewrite the power:
p(t)=E0I02sin(2ωt)
4. Analyze Instantaneous Power:
- The instantaneous power p(t) oscillates between positive and negative values, but it is not zero at all times. Therefore, the statement "instantaneous power is zero" is not true.
5. Calculate Average Power Over a Full Cycle:
- The average power Pavg over one full cycle (T) can be calculated using:
Pavg=1T∫T0p(t)dt
- Substituting the expression for p(t):
Pavg=1T∫T0E0I02sin(2ωt)dt
- The integral of sin(2ωt) over one complete cycle is zero:
∫T0sin(2ωt)dt=0
- Therefore, the average power becomes:
Pavg=E0I02T⋅0=0
6. Conclusion:
- The average power over a full cycle for an ideal inductor connected to a sinusoidal AC source is zero.
Final Answer:
- The quantity that is zero is the average power over a full cycle of the AC voltage source.
- We have an ideal inductor (L) connected to a sinusoidal AC voltage source, which can be represented as e(t)=E0sin(ωt).
- In an inductive circuit, the current lags the voltage by a phase difference of π2 radians. Therefore, the current can be expressed as:
i(t)=I0sin(ωt−π2)=I0cos(ωt)
- The instantaneous power p(t) is given by the product of voltage and current:
p(t)=e(t)⋅i(t)=E0sin(ωt)⋅I0cos(ωt)
- Using the identity sin(x)cos(x)=12sin(2x), we can rewrite the power:
p(t)=E0I02sin(2ωt)
- The instantaneous power p(t) oscillates between positive and negative values, but it is not zero at all times. Therefore, the statement "instantaneous power is zero" is not true.
- The average power Pavg over one full cycle (T) can be calculated using:
Pavg=1T∫T0p(t)dt
- Substituting the expression for p(t):
Pavg=1T∫T0E0I02sin(2ωt)dt
- The integral of sin(2ωt) over one complete cycle is zero:
∫T0sin(2ωt)dt=0
- Therefore, the average power becomes:
Pavg=E0I02T⋅0=0
- The average power over a full cycle for an ideal inductor connected to a sinusoidal AC source is zero.
- The quantity that is zero is the average power over a full cycle of the AC voltage source.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-B52videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C50videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section -E6videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
An inductor-coil having some resistance is connected to an AC source. Which of the following quantities have zero average value over a cycle?
View SolutionIf an ac source is connected across ideal capacitor and current passing through it is denoted by curve (a) then instantaneous power is denoted by curve
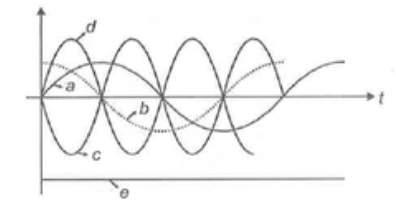 View Solution
View SolutionProve that the current flowing through an ideal inductor connected across a.c. source, lags the voltage in phase by π2.
View SolutionWhich of the following quantities have zero average value over a cycle.If an inductor coil having some resistance is connected to a sinusoidal AC source.
View SolutionIn an AC circuit, voltage V = V0sinωt and inductor L is connected across the circuit. Then the instantaneous power will be
View SolutionWhich of the following is true for an ideal capacitor connected to a sinusoidal voltage source ?
View SolutionIn a series L−R circuit, under which condition the power loss will be least for an a.c voltage source?
View SolutionTwo identical incandescent light bulbs are connected as shown in figure. When the circuit is an AC voltage source of frequency f, which of the following observations will be correct.
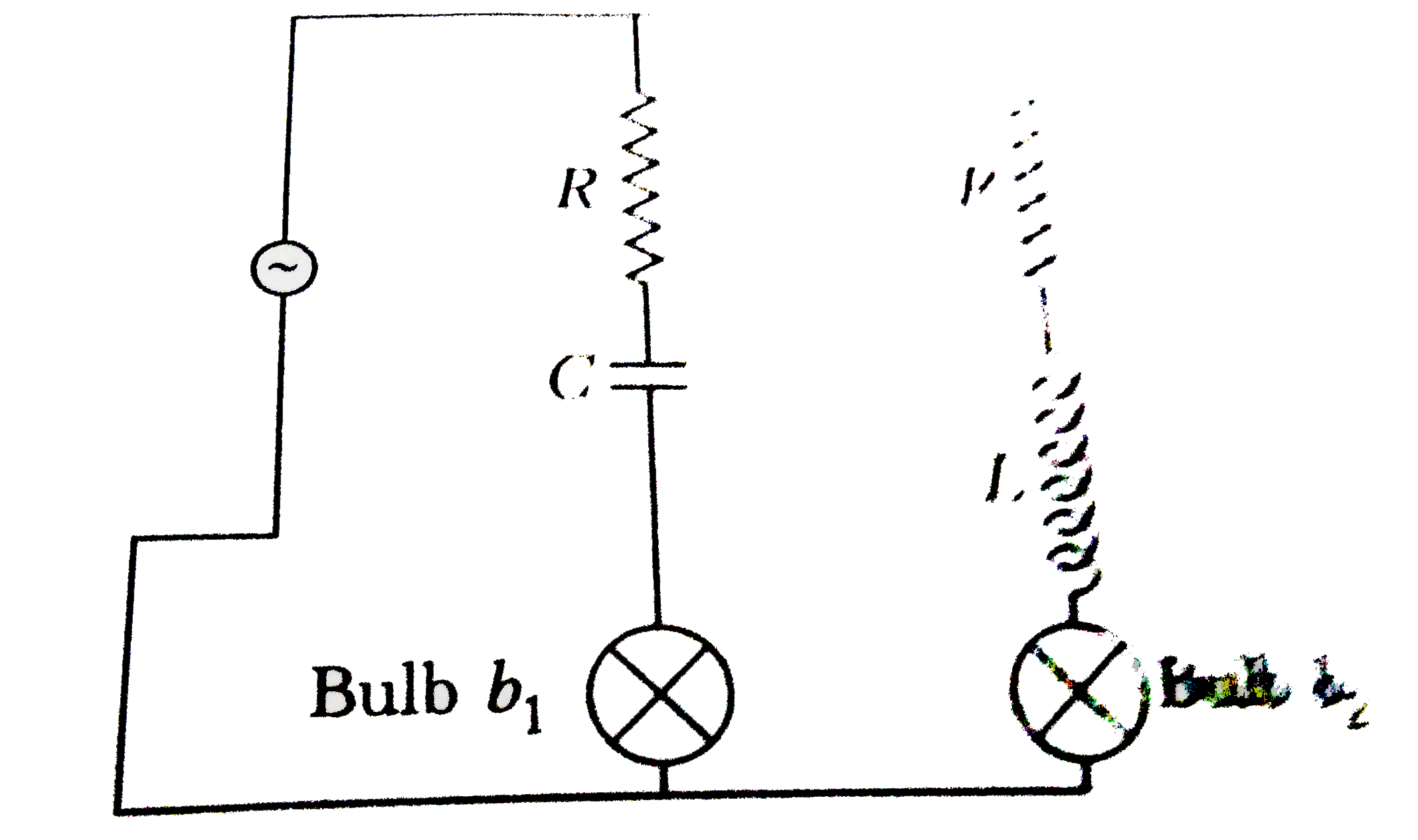 View Solution
View SolutionCan the instantaneous power output of an ac source ever be negative ? Can the average power output be negative ?
View SolutionAn inductor, a capacitor, and a resistor are connected in series. The combination is connected across an ac source.
Statement 1: Peak current through each remains same.
Statement 2: Average power dielivered by source is equal to average power developed across resistance.View Solution
