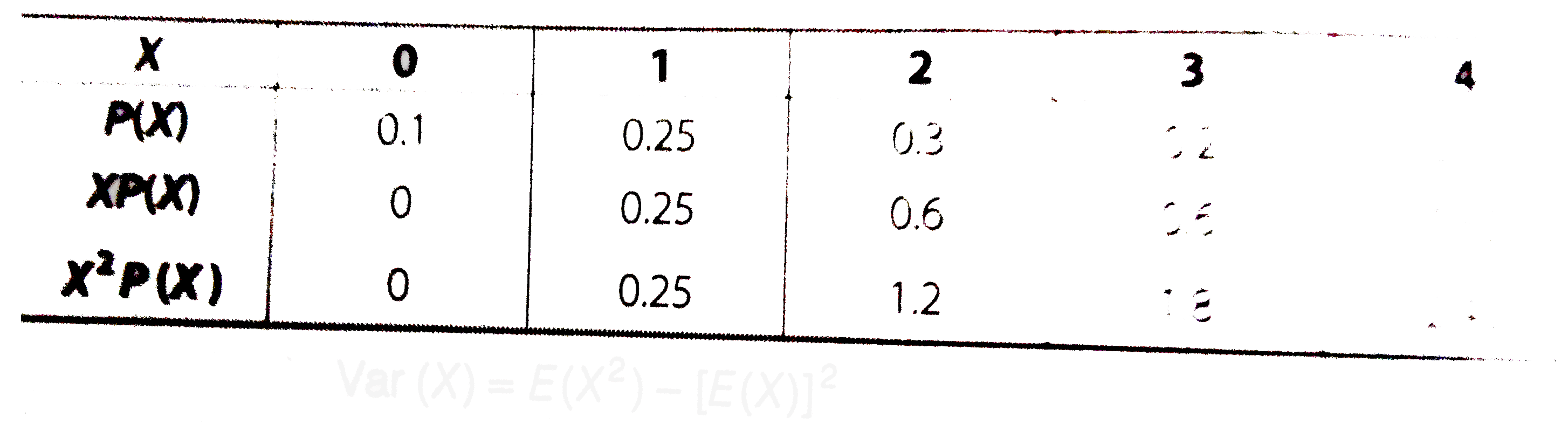
Consider the probability distribution of a random variable X

Calculate
(i) V(X2) (ii) Variance of X.
We have
Var(X)=E(X2)−[E(X)]2
where, E(X)=μ=n∑i=1xiPi(ξ)
and E(X2)=sunni=1xiPi(ξ)
∴E(X)=0+0.25+0.6+0.6+0.60=2.05
E(X2)=0+0.25+1.2+1.8+2.40=5.65
(i) V(X2)=14V(X)=14[5.65−(2.05)2]
=14[56.65−4.2025]=14×1.4775=0.361875
(II) V(X) = 1.4475
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions
15 Videos
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions
38 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers
15 Videos
Similar Questions
Consider the probability distribution of a random variable X.

Variance of X
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
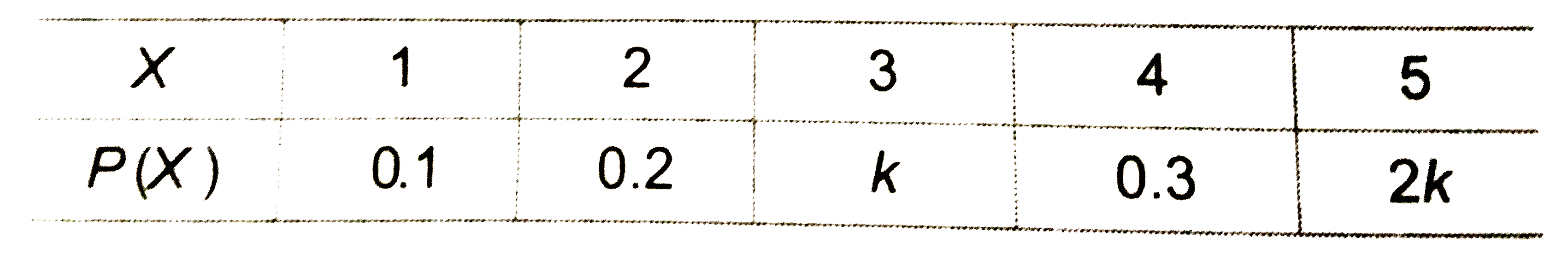
View SolutionIn a probability distribution of a random variable X , the sum of probabilities is always
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe probability distribution for a random variable X is as follows:
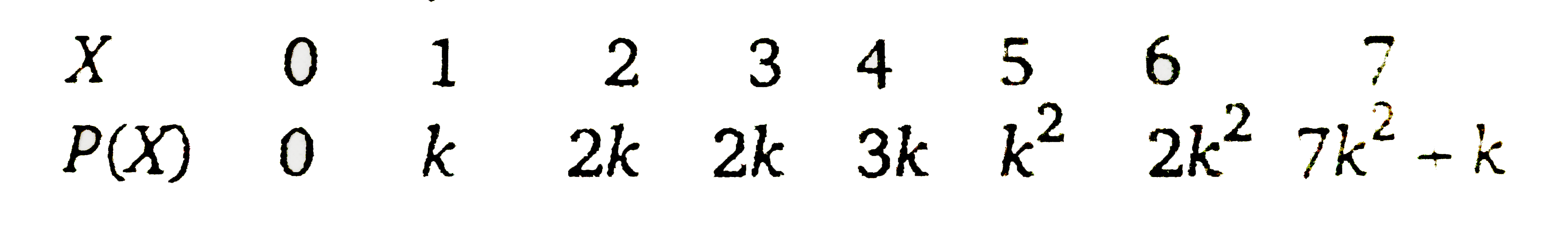
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View Solution
