The probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
The correct Answer is:k=110;P(X<6)=0.81
Step by step video, text & image solution for The probability distribution of a random variable X is given as under: Find k , and P (X lt 6) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MODEL TEST PAPER - 3 BOOK - ICSECHAPTER - MODEL TEST PAPER - 3 EXERCISE - SECTION - B
10 Videos
- MODEL TEST PAPER - 3 BOOK - ICSECHAPTER - MODEL TEST PAPER - 3 EXERCISE - SECTION - C
10 Videos
- MODEL TEST PAPER - 2BOOK - ICSECHAPTER - MODEL TEST PAPER - 2EXERCISE - Section - C
10 Videos
- MODEL TEST PAPER - 4BOOK - ICSECHAPTER - MODEL TEST PAPER - 4EXERCISE - SECTION - C
10 Videos
Similar Questions
The probability distribution of a random variable X is given below.

Find k, mean and variance of X
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionConsider the probability distribution of a random variable X.

Variance of X
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionThe probability distribution of a discrete random variable x is given as under

Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionThe probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionThe probability distribution of a discrete random variable X is given as under: X:1242A3A5A P(X):121/5325110125125 Calculate: The value of A,ifE(X)=2.94 (ii) Variance ofX.
View SolutionThe probability distribution for a random variable X is as follows:
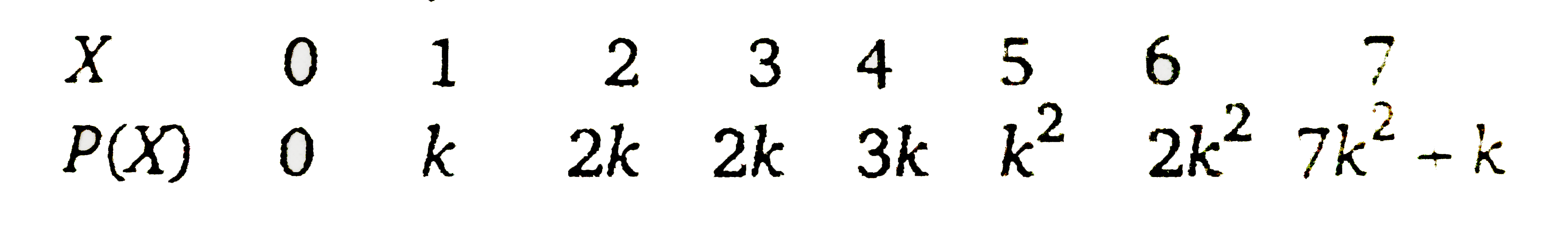
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View Solution
