A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because
The magnetic field is constant
The magnetic field is in the smae plane as the circular coil and it may or may not vary
The magnetic field has a perpendicular ( to the palne of the coil) component whose magnitude is decreasing suitably
There is a constant magnetic fied in the perpendicular ( to the plane of the coil direction)
The correct Answer is:B,C
To solve the question regarding why no electromotive force (EMF) is produced in a circular coil that expands radially in a magnetic field, we can analyze the conditions under which EMF is induced.
1. Understanding EMF and Magnetic Flux:
- The induced EMF (ε) in a coil is given by Faraday's law of electromagnetic induction:
ϵ=−dΦdt
- Here, Φ is the magnetic flux through the coil, defined as:
Φ=B⋅A=B⋅A⋅cos(θ)
- Where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the surface of the coil.
2. Analyzing the Conditions:
- For EMF to be zero, the rate of change of magnetic flux must be zero, which can occur under several conditions:
- The magnetic field B is constant.
- The area A is not changing in a way that affects the flux.
- The angle θ remains constant (specifically, it can be 90 degrees, making cos(90)=0).
3. Evaluating the Options:
- Option A: The magnetic field is constant.
- If the magnetic field is constant and the area is changing, the flux would change, leading to a non-zero EMF. Therefore, this option is incorrect.
- Option B: The magnetic field is in the same plane as the circular coil and may or may not vary.
- If the magnetic field is in the same plane, the angle θ between the magnetic field and the area vector is 90 degrees. Thus, cos(90)=0, leading to zero flux change. This option is correct.
- Option C: The magnetic field has a perpendicular component whose magnitude is decreasing suitably.
- If there is a perpendicular component of the magnetic field and its magnitude is decreasing, while the area is increasing, the overall flux can remain constant if the changes balance each other out. This can also lead to zero EMF. Thus, this option is correct.
- Option D: There is a constant magnetic field in the perpendicular direction to the plane of the coil.
- If the magnetic field is constant and perpendicular, the area is changing, leading to a change in flux and a non-zero EMF. Therefore, this option is incorrect.
4. Conclusion:
- The correct options that explain why no EMF is produced in the expanding circular coil are Option B and Option C.
- The induced EMF (ε) in a coil is given by Faraday's law of electromagnetic induction:
ϵ=−dΦdt
- Here, Φ is the magnetic flux through the coil, defined as:
Φ=B⋅A=B⋅A⋅cos(θ)
- Where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the surface of the coil.
- For EMF to be zero, the rate of change of magnetic flux must be zero, which can occur under several conditions:
- The magnetic field B is constant.
- The area A is not changing in a way that affects the flux.
- The angle θ remains constant (specifically, it can be 90 degrees, making cos(90)=0).
- Option A: The magnetic field is constant.
- If the magnetic field is constant and the area is changing, the flux would change, leading to a non-zero EMF. Therefore, this option is incorrect.
- Option B: The magnetic field is in the same plane as the circular coil and may or may not vary.
- If the magnetic field is in the same plane, the angle θ between the magnetic field and the area vector is 90 degrees. Thus, cos(90)=0, leading to zero flux change. This option is correct.
- Option C: The magnetic field has a perpendicular component whose magnitude is decreasing suitably.
- If there is a perpendicular component of the magnetic field and its magnitude is decreasing, while the area is increasing, the overall flux can remain constant if the changes balance each other out. This can also lead to zero EMF. Thus, this option is correct.
- Option D: There is a constant magnetic field in the perpendicular direction to the plane of the coil.
- If the magnetic field is constant and perpendicular, the area is changing, leading to a change in flux and a non-zero EMF. Therefore, this option is incorrect.
- The correct options that explain why no EMF is produced in the expanding circular coil are Option B and Option C.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - very short answer
6 Videos
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Short answer type questions
5 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question
6 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
Similar Questions
A circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA 50 turns circular coil has a radius of 3 cm, it is kept in a magnetic field acting normal to the area of the coil. The magnetic field B increased from 0.10 tesla to 0.35 tesla in 2 milliseconds. The average induced e.m.f in the coil is
View Solution
Knowledge Check
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 Nm
Magnetic Field due to Circular Coil
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View SolutionA circular coil carrying current I is placed in a region of uniform magnetic field acting perpendicular to a coil as shown in te Mark correct option
 .
.
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
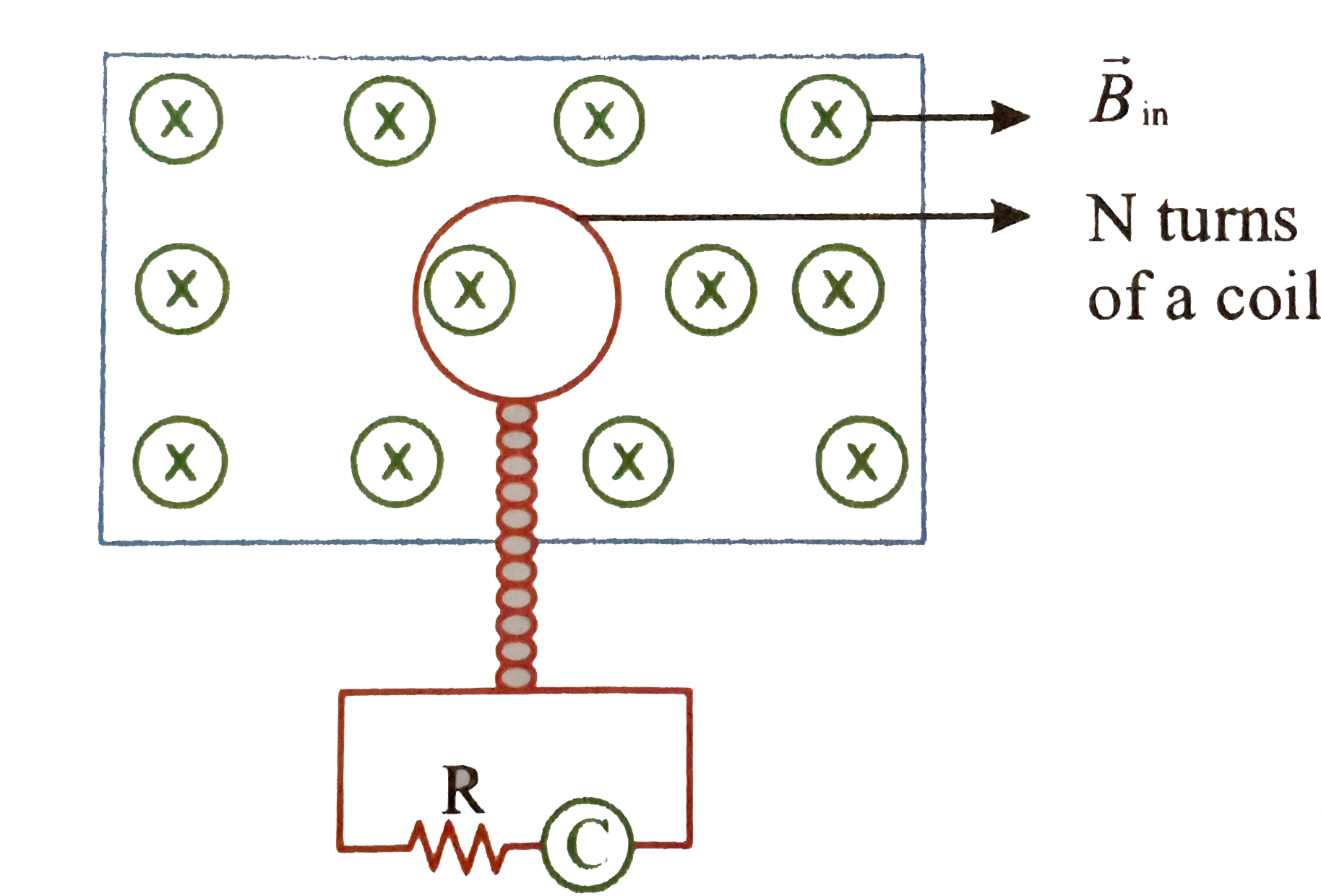
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View Solution
