An open box with a square base is to be made out of a given quantity of card board of area c2 square units. Show that the maximum volume of the box is c36√3 cubic units.
To solve the problem of finding the maximum volume of an open box with a square base made from a given area of cardboard c2, we can follow these steps:
Step 1: Define the Variables
Let the side length of the square base be x and the height of the box be y.
Step 2: Write the Volume Formula
The volume V of the box can be expressed as:
V=x2y
Step 3: Write the Surface Area Constraint
The surface area of the open box consists of the base and the four sides. The area of the base is x2 and the area of the four sides is 4xy. Thus, the total area constraint is:
x2+4xy=c2
Step 4: Express y in Terms of x
From the surface area constraint, we can solve for y:
4xy=c2−x2⟹y=c2−x24x
Step 5: Substitute y into the Volume Formula
Substituting y into the volume formula gives:
V=x2(c2−x24x)=x(c2−x2)4
This simplifies to:
V=c2x4−x34
Step 6: Differentiate the Volume Function
To find the maximum volume, we differentiate V with respect to x:
dVdx=c24−3x24
Step 7: Set the Derivative to Zero
Setting the derivative equal to zero to find critical points:
c24−3x24=0⟹c2=3x2⟹x2=c23
Thus,
x=c√3
Step 8: Determine the Nature of the Critical Point
To confirm that this critical point gives a maximum, we can find the second derivative:
d2Vdx2=−32x
Since x>0, d2Vdx2<0, indicating a maximum.
Step 9: Find the Height y
Substituting x=c√3 back into the equation for y:
y=c2−x24x=c2−c234⋅c√3=2c234⋅c√3=2c√312=c2√3
Step 10: Calculate the Maximum Volume
Now substituting x and y back into the volume formula:
V=x2y=(c23)(c2√3)=c36√3
Conclusion
Thus, the maximum volume of the box is:
c36√3
Let the side length of the square base be x and the height of the box be y.
The volume V of the box can be expressed as:
V=x2y
The surface area of the open box consists of the base and the four sides. The area of the base is x2 and the area of the four sides is 4xy. Thus, the total area constraint is:
x2+4xy=c2
From the surface area constraint, we can solve for y:
4xy=c2−x2⟹y=c2−x24x
Substituting y into the volume formula gives:
V=x2(c2−x24x)=x(c2−x2)4
This simplifies to:
V=c2x4−x34
To find the maximum volume, we differentiate V with respect to x:
dVdx=c24−3x24
Setting the derivative equal to zero to find critical points:
c24−3x24=0⟹c2=3x2⟹x2=c23
Thus,
x=c√3
To confirm that this critical point gives a maximum, we can find the second derivative:
d2Vdx2=−32x
Since x>0, d2Vdx2<0, indicating a maximum.
Substituting x=c√3 back into the equation for y:
y=c2−x24x=c2−c234⋅c√3=2c234⋅c√3=2c√312=c2√3
Now substituting x and y back into the volume formula:
V=x2y=(c23)(c2√3)=c36√3
Thus, the maximum volume of the box is:
c36√3
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - OBJECTIVE TYPES QUESTIONS
25 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers
5 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers
5 Videos
- APPLICATION OF INTEGRALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Objective Type Questions
22 Videos
Similar Questions
OR An open box with a square base is to be made out of a given quantity of cardboard of area c2 square units. Show that the maximum volume of the box is c36 √3 cubic units.
View SolutionA square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Also, find the maximum volume.
View Solution
Knowledge Check
A rectangular box with an open top is constructed from cardboard to have a square base of area x2 and height h. If the volume of this box is 50 cubic units, how many square units of cardboard in terms of x, are needed to build this box ?
A5x2B6x2C200x+x2D200x+2x2A 3-inch-tall rectangular box with a square base is constructed to hold a circular pie that has a diameter of 8 inches. Both are shown below. What is the volume, in cubic inches, of the smallest such box that can hold this pie?
 A24B64C72D192
A24B64C72D192
If A(x,y),B(1,2)andC(2,1) are the vertices of a triangle of area 6 square units, show that x+y=15 or −9.
View SolutionA pyramid with vertex at point P has a regular hexagonal base ABCDEF , Position vector of points A and B are ˆiandˆi+2ˆj The centre of base has the position vector ˆi+ˆj+√3ˆk. Altitude drawn from P on the base meets the diagonal AD at point G. find the all possible position vectors of G. It is given that the volume of the pyramid is 6√3 cubic units and AP is 5 units.
View SolutionThe volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
View SolutionA square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
View Solution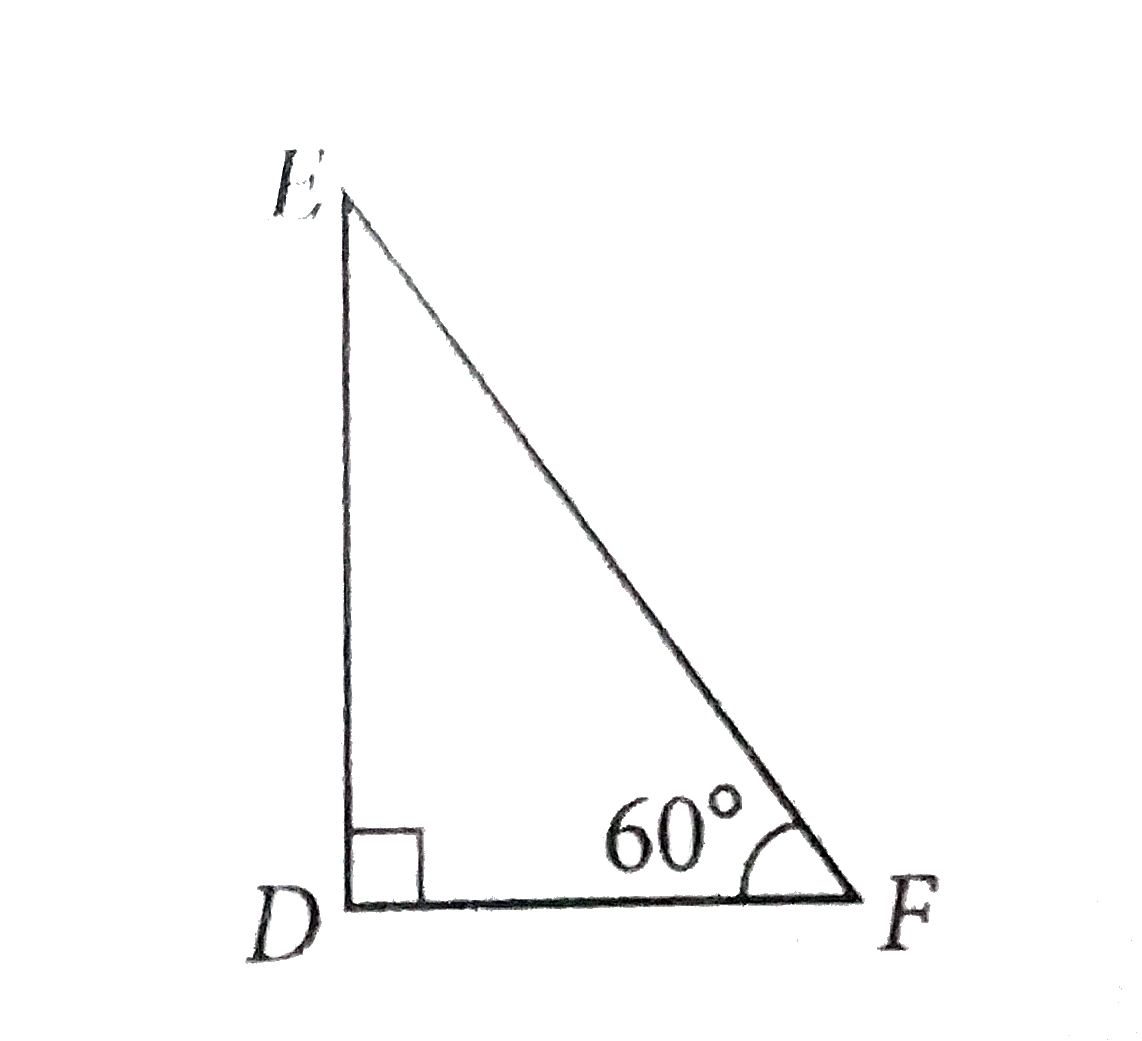
The area of triangle DEF is 32√3 square units. What is the length of ¯¯¯¯¯¯DF?
View SolutionAn open tank is to be constructed with square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead will be least, if depth is made half of width.
View Solution