Find the locus of the mid-point of the portion of the line $x cos α + y sin α = p$ which is intercepted between the axes.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

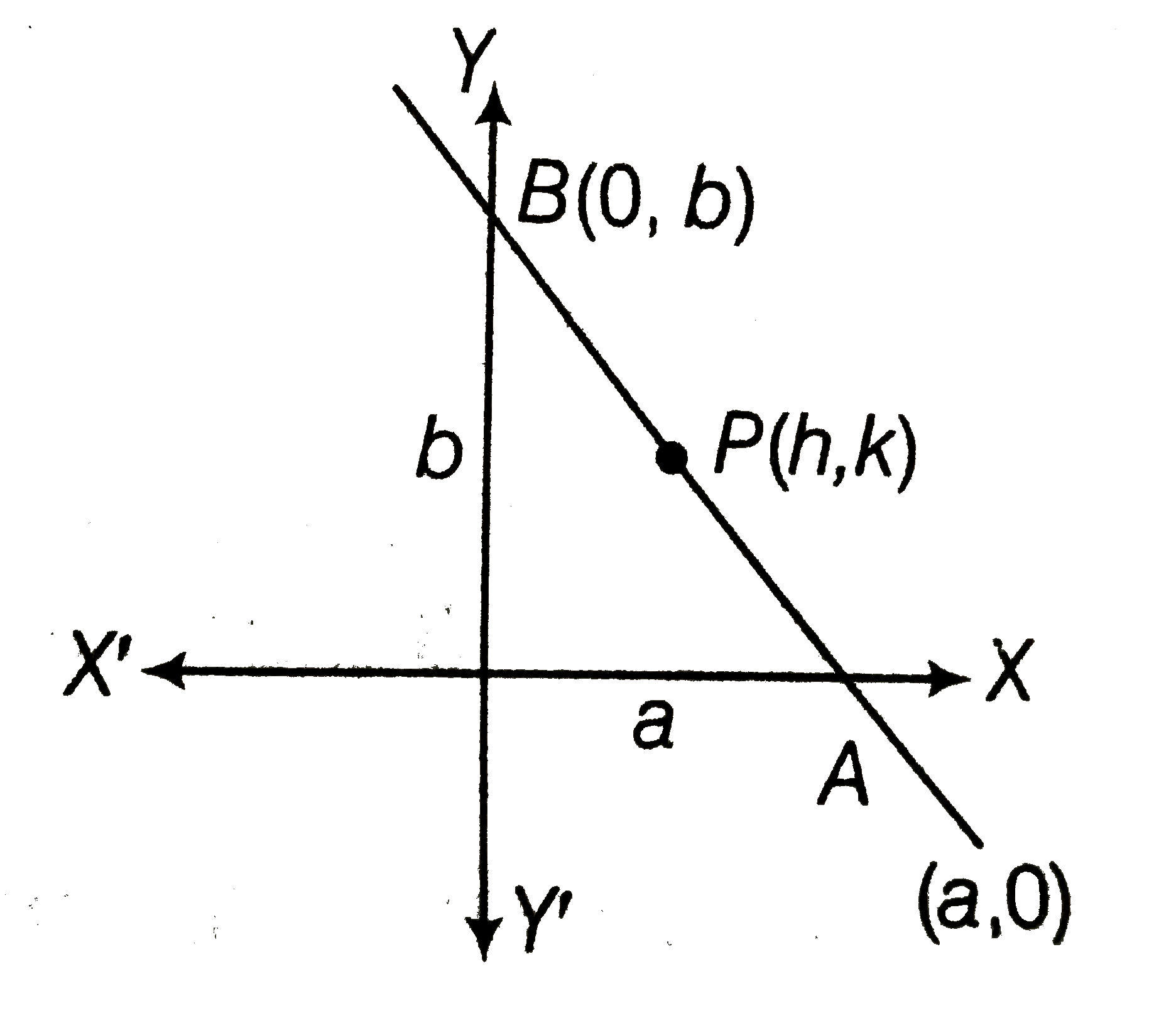
Given equation of the line is $x sin θ + y cos θ = p$
Let the mid-point of AB is p(h,k).
So, the mid-point of AB are $(\frac{a}{2}, \frac{b}{2})$
Since, the point (a,0) lies on the line (i), then $a sin θ + 0 = p$
$\Rightarrow a sin θ = p \Rightarrow a = \frac{p}{sin θ}$
and the point (0,b) also lies on the line then, $0 + b cos θ = p$
$\Rightarrow b cos θ = p \Rightarrow a = (p) . (sin θ)$
Now, mid-point of $A B = (\frac{a}{2}, \frac{a}{2})$ or $(\frac{p}{2 sin θ}, \frac{p}{2 cos θ})$
$∵ \frac{p}{2 sin θ} = h \Rightarrow sin θ = \frac{p}{2 h}$
$\Rightarrow 1 = \frac{p^{2}}{4} (\frac{1}{h^{2}} + \frac{1}{k^{2}})$
Locus of the mid-point is
$4 = p^{2} (\frac{1}{x^{2}} + \frac{1}{y^{2}})$
$\Rightarrow 4 x^{2} y^{2} = p^{2} (x^{2} + y^{2})$

Updated on:21/07/2023

|

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-STRAIGHT LINES-Fillers

Home
Ask Doubt
Profile