If a+ib=c+, then
a2+c2=0
b2+c2=0
b2+d2=0
a2+b2=c2+d2
The correct Answer is:D
To solve the equation a+ib=c+id, we will follow these steps:
Step 1: Understand the Equation
We start with the equation:
a+ib=c+id
This means that the complex number on the left side is equal to the complex number on the right side.
Step 2: Separate Real and Imaginary Parts
From the equation, we can separate the real and imaginary parts:
- Real part: a=c
- Imaginary part: b=d
Step 3: Take the Modulus of Both Sides
Next, we take the modulus of both sides of the equation:
|a+ib|=|c+id|
The modulus of a complex number z=x+iy is defined as:
|z|=√x2+y2
So we can express the moduli as:
|a+ib|=√a2+b2
|c+id|=√c2+d2
Step 4: Set the Moduli Equal
Now we set the moduli equal to each other:
√a2+b2=√c2+d2
Step 5: Square Both Sides
To eliminate the square roots, we square both sides:
a2+b2=c2+d2
Conclusion
Thus, we have derived the equation:
a2+b2=c2+d2
This is the final result.
We start with the equation:
a+ib=c+id
This means that the complex number on the left side is equal to the complex number on the right side.
From the equation, we can separate the real and imaginary parts:
- Real part: a=c
- Imaginary part: b=d
Next, we take the modulus of both sides of the equation:
|a+ib|=|c+id|
The modulus of a complex number z=x+iy is defined as:
|z|=√x2+y2
So we can express the moduli as:
|a+ib|=√a2+b2
|c+id|=√c2+d2
Now we set the moduli equal to each other:
√a2+b2=√c2+d2
To eliminate the square roots, we square both sides:
a2+b2=c2+d2
Thus, we have derived the equation:
a2+b2=c2+d2
This is the final result.
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - TRUE/FALSE
9 Videos
- BINOMIAL THEOREMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - True/False
7 Videos
- CONIC SECTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - Objective type
13 Videos
Similar Questions
Knowledge Check
In a transistor connected in a common emitter mode RC=4kΩ,R1=1kΩ,IC=1mA and IB=20μA. Find the voltage gain.
A100B200C300D400
If the roots of Quadratic i2x2+5ix−6 are a+ib and c+ (a,b,c,d∈R and i=√−1) then, (ac−bd)+(ad+bc)i=?
View SolutionIf z1=a+ibandz2=c+ are complex numbers such that |z1|=|z2|=1andRe(z1¯z2)=0 , then the pair ofcomplex nunmbers ω1=a+icandω2=b+ satisfies
View SolutionIf z 1 =a+ib and z 2 =c+id are complex numbers such that ∣z 1 ∣=∣z 2 ∣=1 and Re(z 1 z 2 )=0, then the pair of complex numbers w 1 =a+ic and w 2 =b+id satisfy
View SolutionSuppose three real numbers a, b, c are in G.P. Let z=a+ibc−ib. Then
View SolutionIn the circuit shown in figure when the input voltage of the base resistance is 10 V . Find the values of Ib,Icandβ .
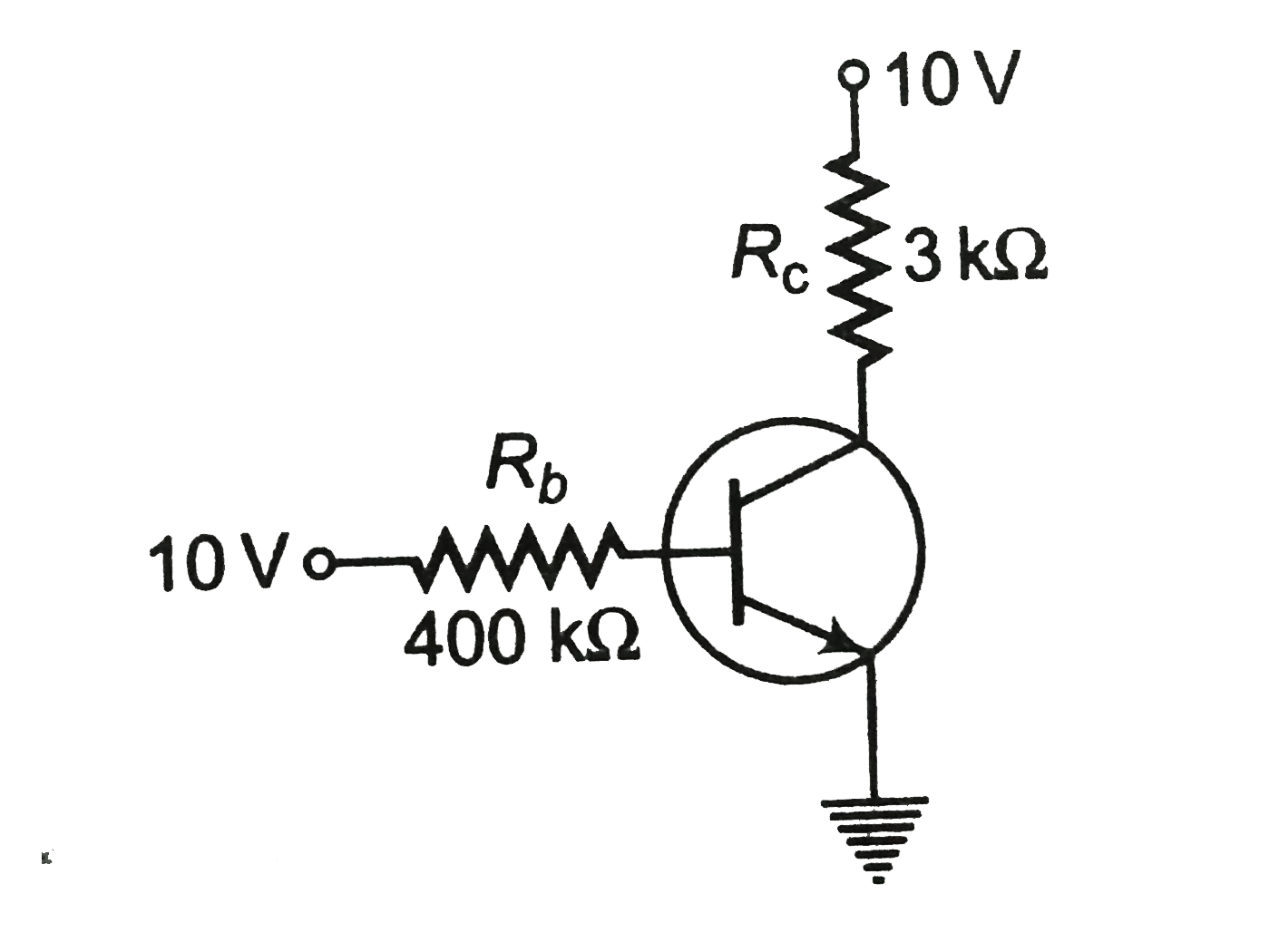
View SolutionIf (a+ib)=1+i1−i, then prove that (a2+b2)=1
View SolutionExpress the following in the form of a + ib .
(i) (14+4i)2
View Solution
