Match the AP's given in column A with suitable common differences given in column B.

A1.2,−2,−6,−10,…
Here, common difference, d=−2−2=−4
A2.∵an=a+(n−1)d
⇒0=−18+(10−1)d
18=9d
∴ Common difference, d=2
A3.∵a10=6
⇒a+(10−1)d=6
⇒ 0+9d=6 [∵a=0(given)]
⇒ 9d=6⇒d=23
A4.∵a2=13
⇒a+(2−1)d=13 [∵an=a+(n−1)d]
⇒ a+d=13 ...(i)
and a4=3⇒a+(4−1)d=3
∴ a+3d=3 ...(ii)
On subtracting Eq. (i) from Eq. (ii), we get
2d=−10
⇒d=−5
∴(A1)→B4,(A2)→B5,(A3)→B1 and (A4)→B2
Topper's Solved these Questions
- ARITHMETIC PROGRESSIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions
10 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Very Short Answer Type Questions
8 Videos
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Long Answer Type Questions
20 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
14 Videos
Similar Questions
Match the items given in column A and B:
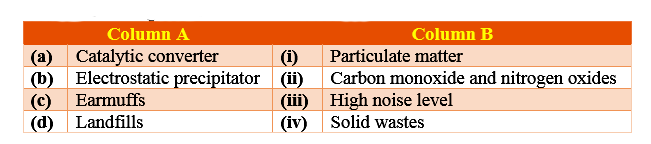
View SolutionMatch the polymers given in column I with their commerical names given in column II

View SolutionMatch the reactions given in Column I with the suitable reagents given in Column II.

View SolutionMatch the terms given in column 'A' with the descriptive phrase given in column 'B' .

View SolutionMatch the terms given in column 'A' with the descriptive phrase given in column 'B' .

View SolutionMatch the terms given in column 'A' with the descriptive phrase given in column 'B' .
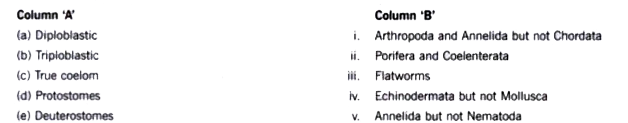
View SolutionMatch the scientists given in column 'A' with the statements given in column 'B'.

View SolutionMatch the polymers given in column I with their main applications given in column II

View SolutionMatch structures given in Column I with the type of detergents given in Column II.

View SolutionMatch the polymers given in column I with their repeating units given in column II
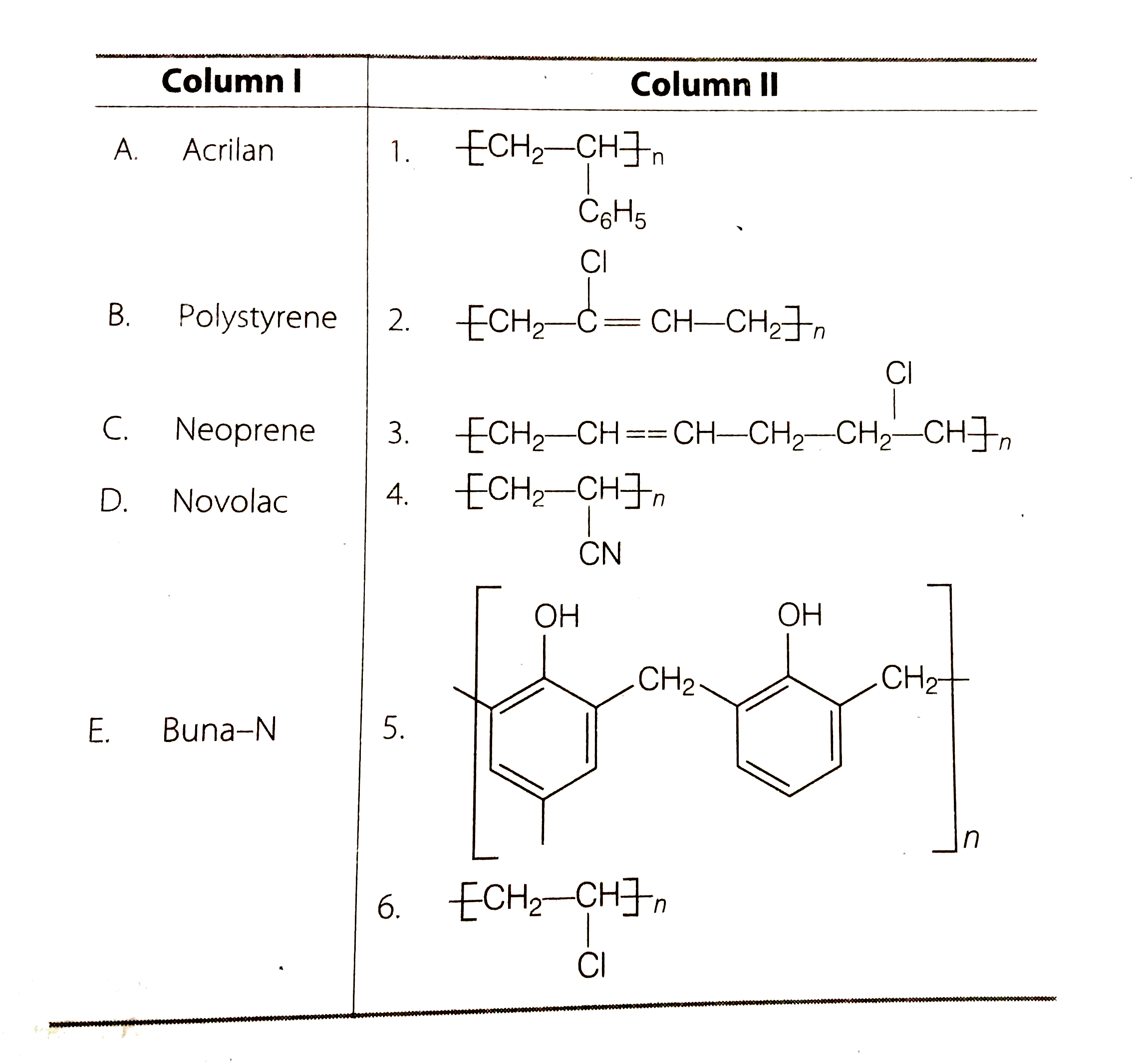
View Solution
