about to only mathematics

Video Solution

Text Solution

Verified by Experts

Let OQ=x and OA=y
Given that, BQ=q, SA=P and AB=SQ=Length of ladder
Also, $∠ B A O = α$ and $∠ Q S O = β$
Now, in $Δ Q S O$
$cos β = \frac{O S}{S Q}$
$\Rightarrow O S = S q cos β = A b cos β$ $[∴ A B = S Q]$ ………….(iii)
and $sin β = \frac{O Q}{S Q}$
$\Rightarrow O Q = S Q sin β - A B sin β$ $[∴ A B = S Q]$ ...............(iv)

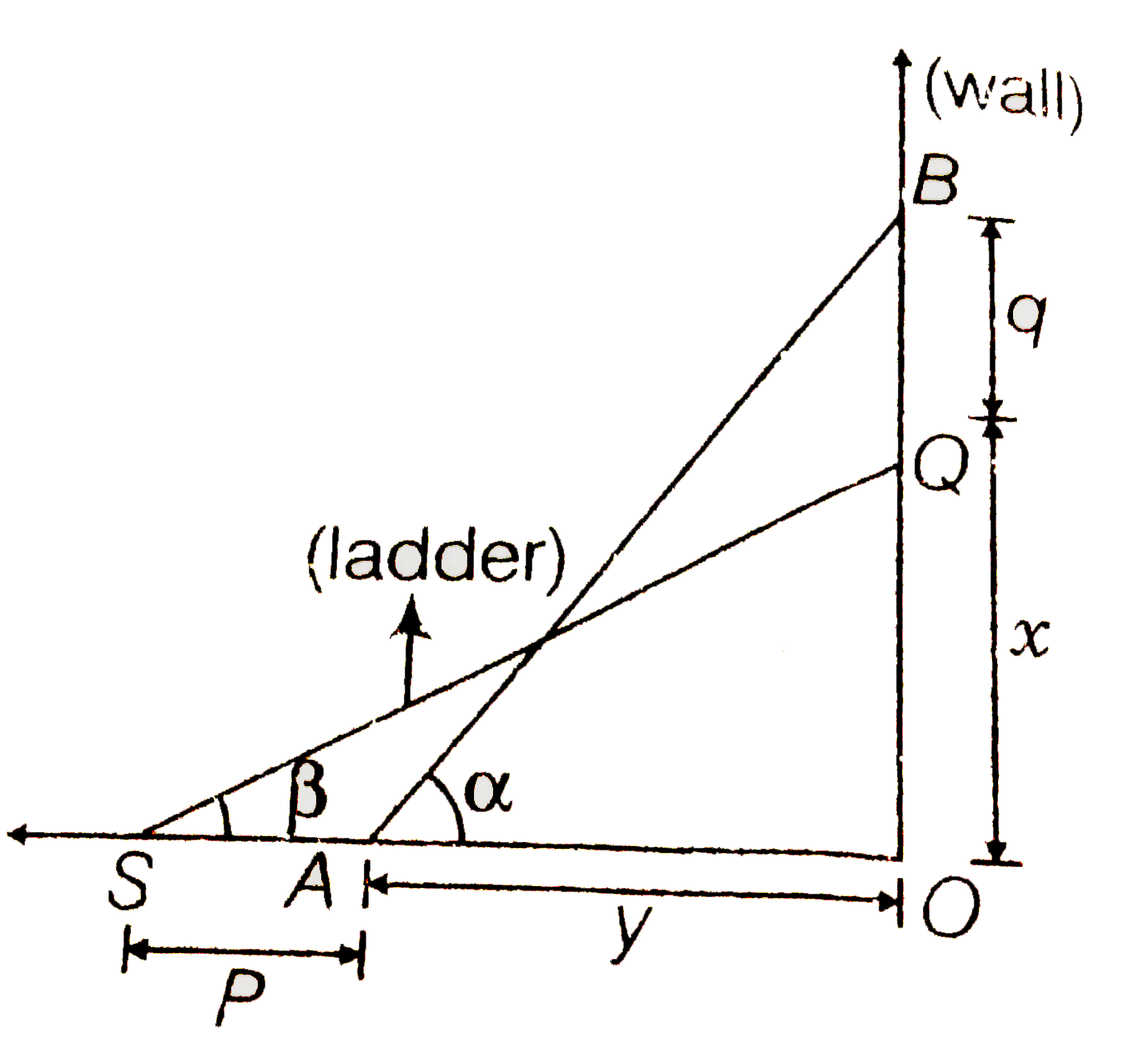
Now, SA=OS-AO
$P = A B cos β - A B cos α$
$\Rightarrow P = A B (cos β - cos α)$ ............(v)
and BQ=BO-QO
$\Rightarrow q = B A (sin α - sin β)$ ..............(vi)
Eq. (v) divided by Eq.(vi), we get
$\frac{p}{q} = \frac{A B (cos β - cos α)}{A B (sin α - sin β)} = \frac{cos β - cos α}{sin α - sin β}$
$\Rightarrow \frac{p}{q} = \frac{cos β - cos α}{sin α - sin β}$ Hence proved.

Updated on:21/07/2023