The shadow of a tower standing on a level ground is found to be 40 m longer when the Suns altitude is 30o than when it is 60o. Find the height of the tower.
Let the height of the tower be h and RQ=x m
Given that, PR=50 m
and ∠SPQ=30∘,∠SRQ=60∘
Now, in ΔSRQ, tan60∘=SQRQ
⇒√3=hx⇒x=h√3……………(i)
and in ΔSPQ, tan30∘=SQPQ=SQPR+RQ=h50+x
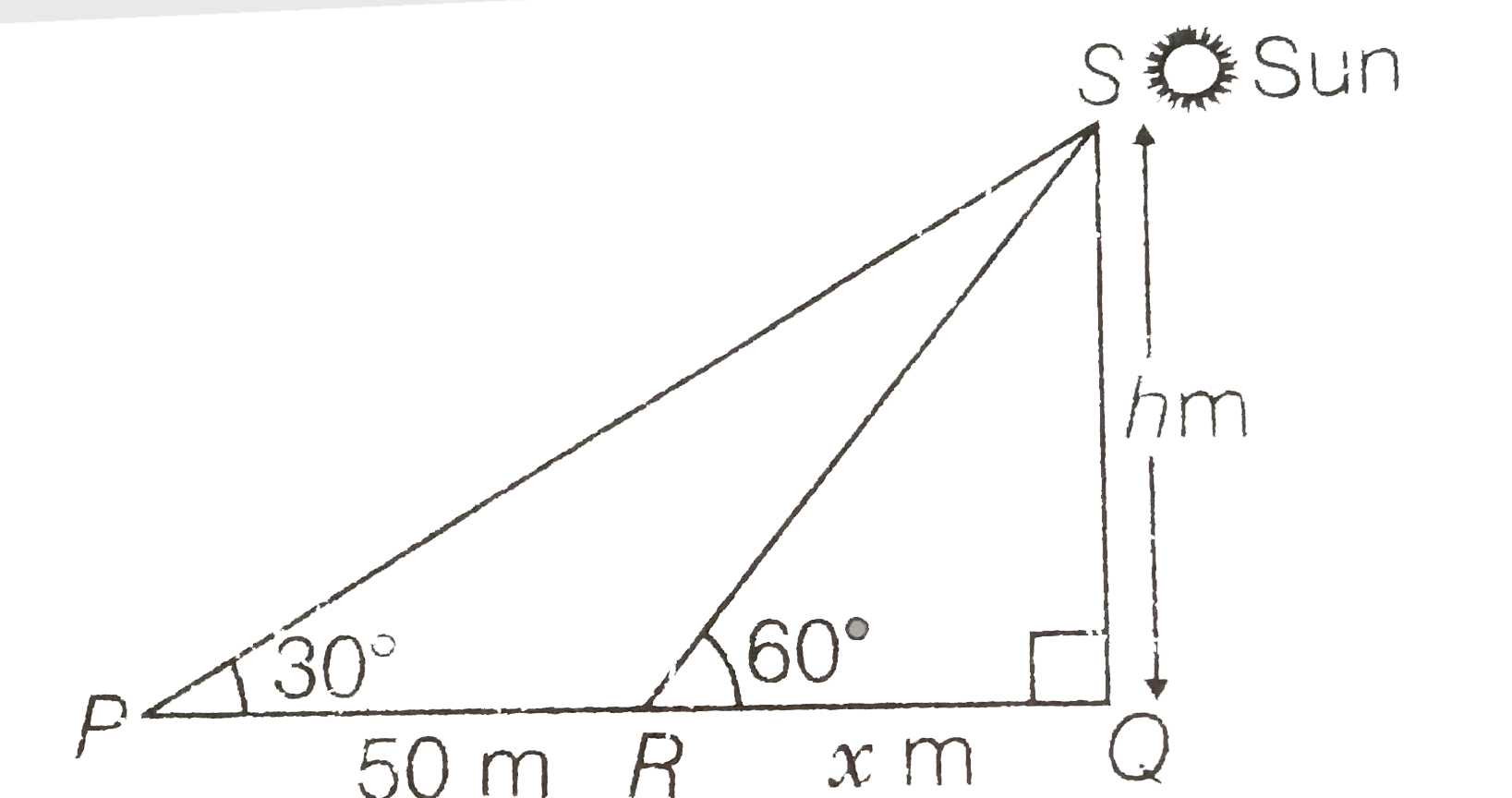
⇒1√3=h50+x
⇒√3.h=50+x
⇒√3.h=50+h√3 [From Eq. (i)]
⇒(√3−1√3)h=50
⇒3−1√3h=50
∴h=50√32
h=25√3m
Hence, the required height of tower is 25√3m
Topper's Solved these Questions
- INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - SHORT ANSWER TYPE QUESTIONS
15 Videos
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 7.4 Long Answer Type Questions
6 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 3.4 Long Answer Type Questions
13 Videos
Similar Questions
The shadow of a tower standing on a level ground is found to be 40m longer when Suns altitude is 30o than when it was 60o . Find the height of the tower.
View SolutionThe shadow of a tower standing on a level plane is found to be 50 m longer when when sun's elevation is 30∘ than when it is 60∘. Find the height of the tower.
View SolutionThe length of the shadow of a tower standing on level ground is found to be 2x metres longer when the suns elevation is 30o than when it was 45o . The height of the tower in metres is (√3+1)x (b) (√3−1)x (c) 2√3x (d) 3√2x
View SolutionThe length of the shadow of a tower standing on level plane is found to be 2x metres longer when the suns altitude is 30o than when it was 45o . Prove that the height of tower is x(√3+1) metres.
View SolutionThe length of the shadow of a tower standing of level plane is found to be 2y metres longer when the sun's altitude is 30∘ then when it was 45∘ . Prove that the height of the tower is y(√3+1) metres
View SolutionThe shadow of a tower, when the angle of elevation of the sun is 45o , is found to be 10m. longer than when it was 60o . Find the height of the tower.
View SolutionThe shadow of a vertical tower on level ground increases by 10 metres, when the altitude of the sun changes from angle of elevatin 450→300. Find the height of the tower, correct to one place of decimal. (Take√3=1.73
View SolutionThe shadow of a pole of height (√3+1) metres standing on the ground is found is found to be 2 metres longer when the elevation is 30∘ than when elevation was α.Then , α=
View SolutionA person observed the angle of elevation of the top of a tower as 30∘ . He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point A on the ground is 30∘. On walking 20 meters toward the tower, the angle of elevation is 60∘. Find the height of the tower and its distance from A.
View Solution
