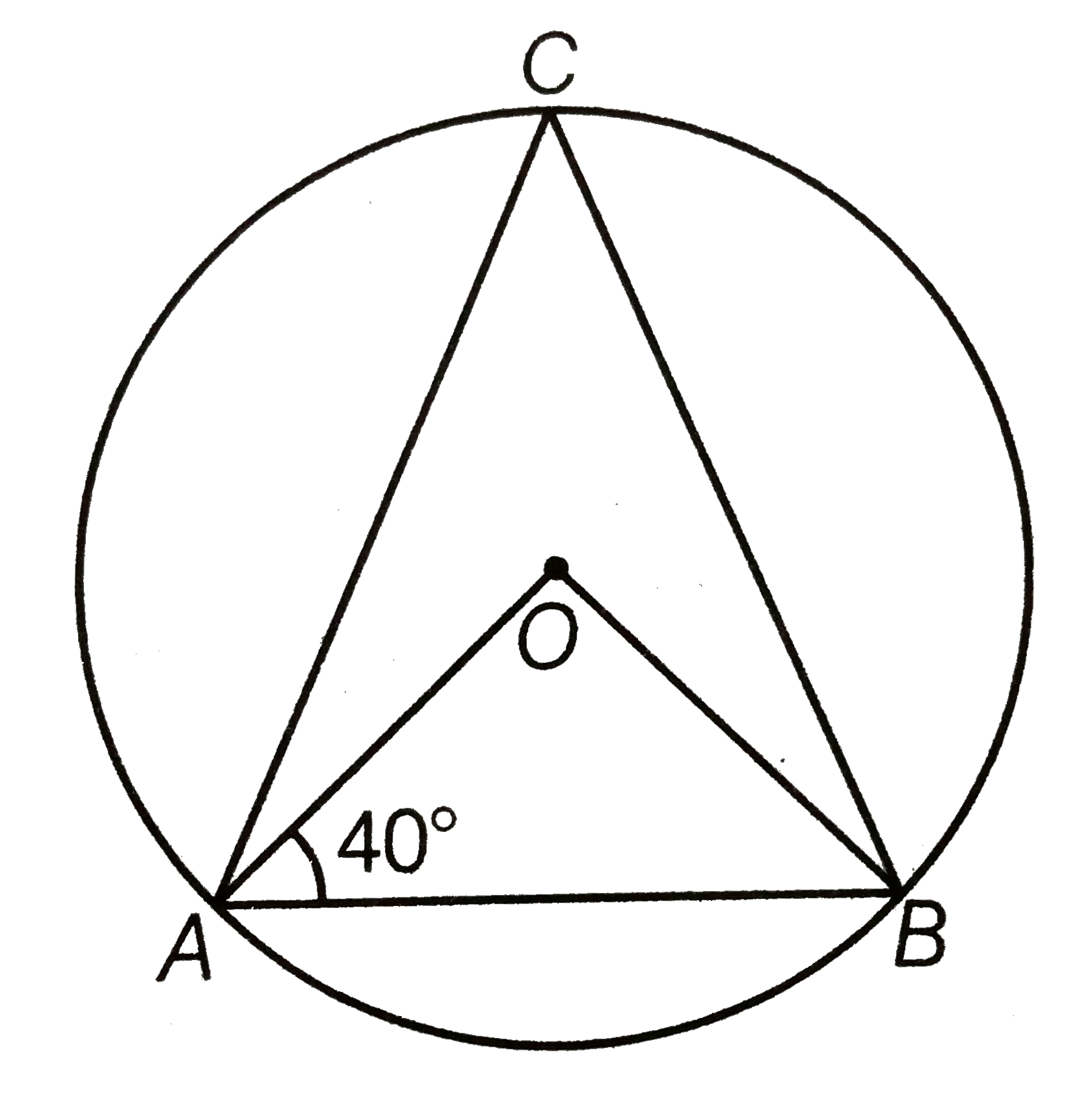
In figure, if ∠OAB=40∘,then∠ACB is equal to
50∘
40∘
60∘
70∘
The correct Answer is:A
In ΔOAB,OA=OB[both are the radius of a circle]
∴∠OAB=∠OBA⇒∠OBA=40∘
[angle opposite to equal sides are equal]
Also, ∠AOB+∠OBA+∠BAO=180∘
[by angle sum property of a triangle]
∴∠AOB+40∘+40∘=180∘
⇒∠AOB=180∘−80∘=100∘
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴∠AOB=2∠ACB
⇒100∘=2∠ACB
∴∠ACB=100∘2=50∘
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.2
Explore 10 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.3
Explore 20 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.4 Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
Similar Questions
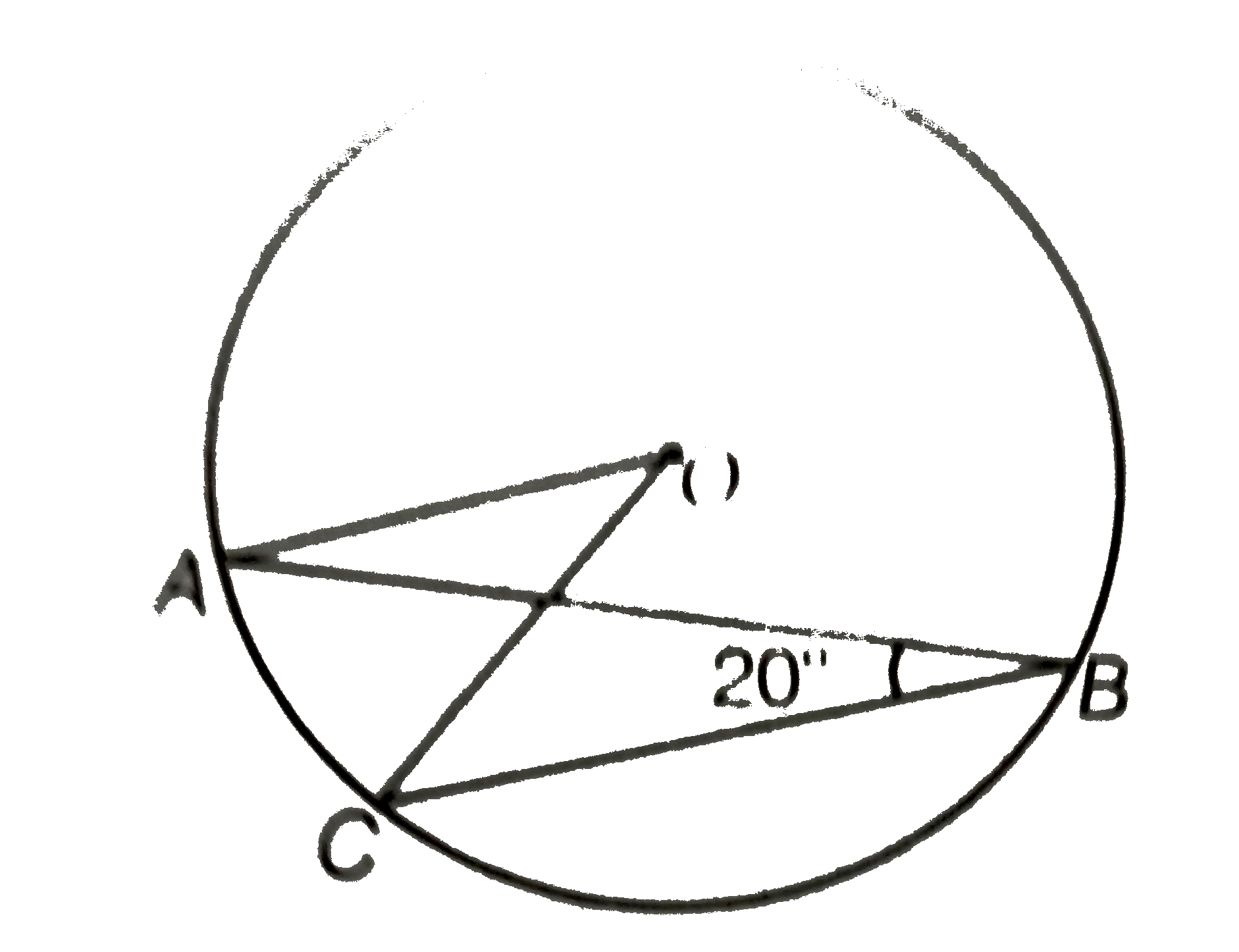
If figure, if∠ABC=20∘,then∠AOC is equal to
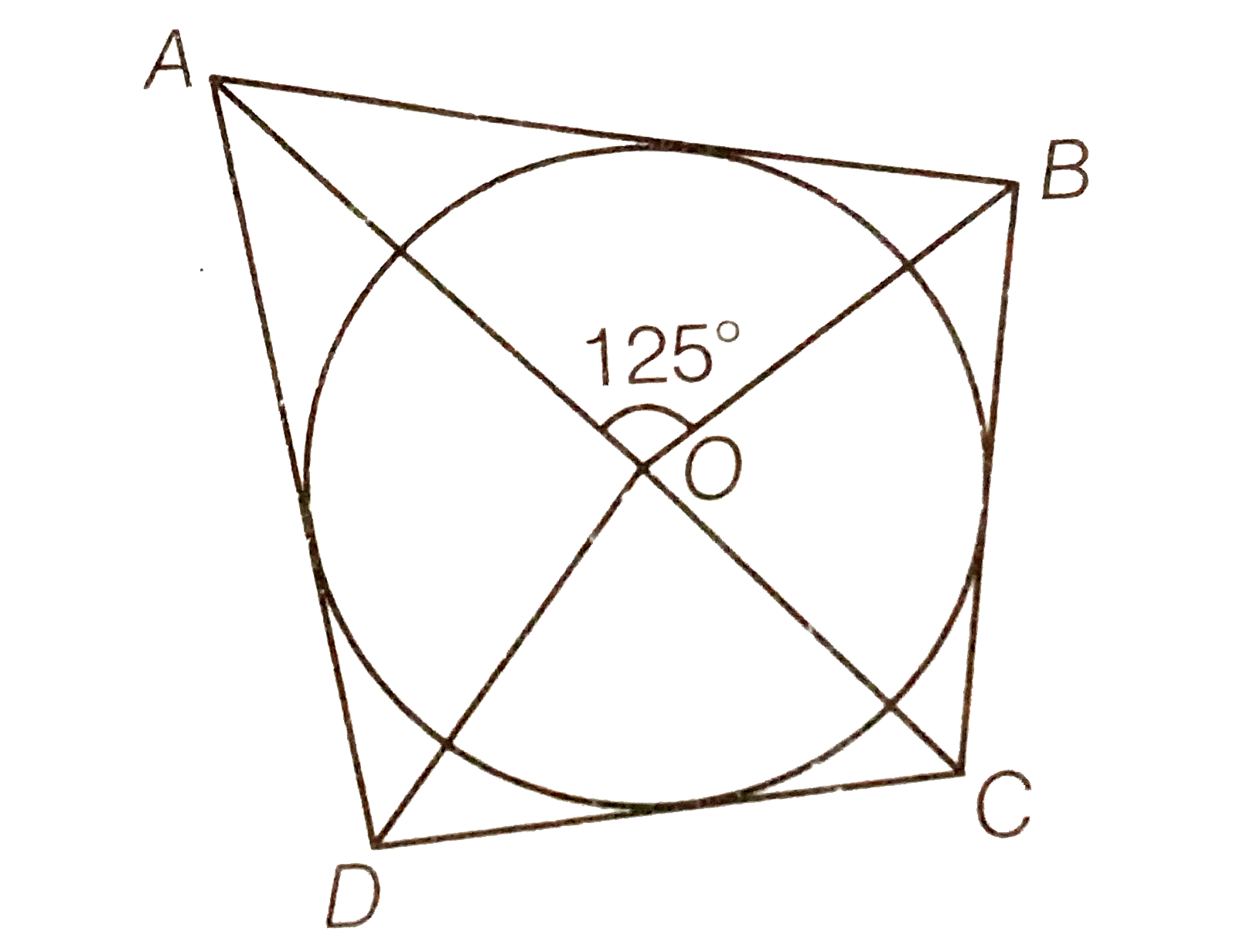
View SolutionIn figure, if ∠AOB=125∘,then∠COD is equal to
View SolutionIn figure, ∠ACB=40∘. Find ∠OAB.

View SolutionIn figure, if ∠DAB=60∘,∠ABD=50∘,then ∠ACB is equal to

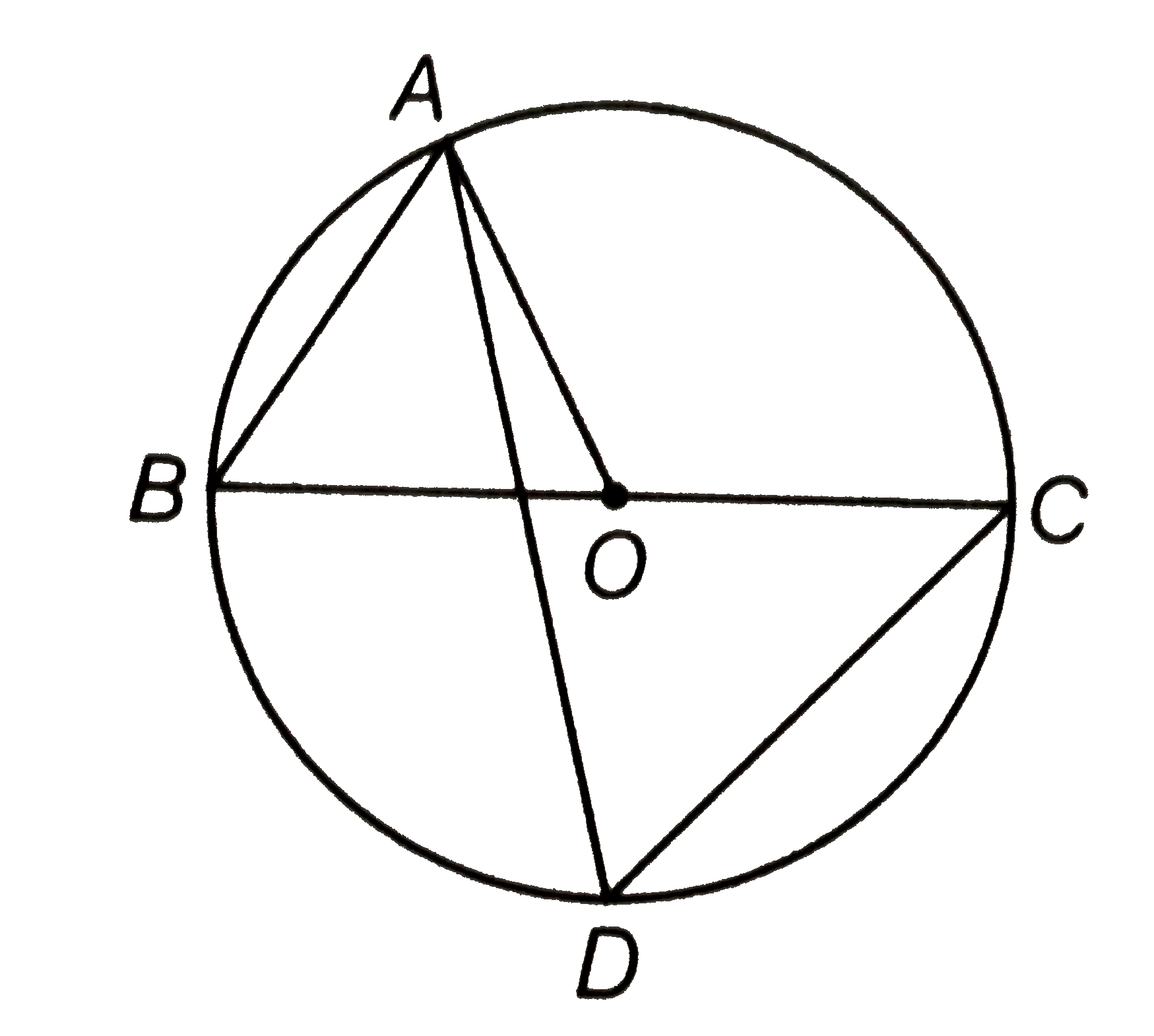
View SolutionIn figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
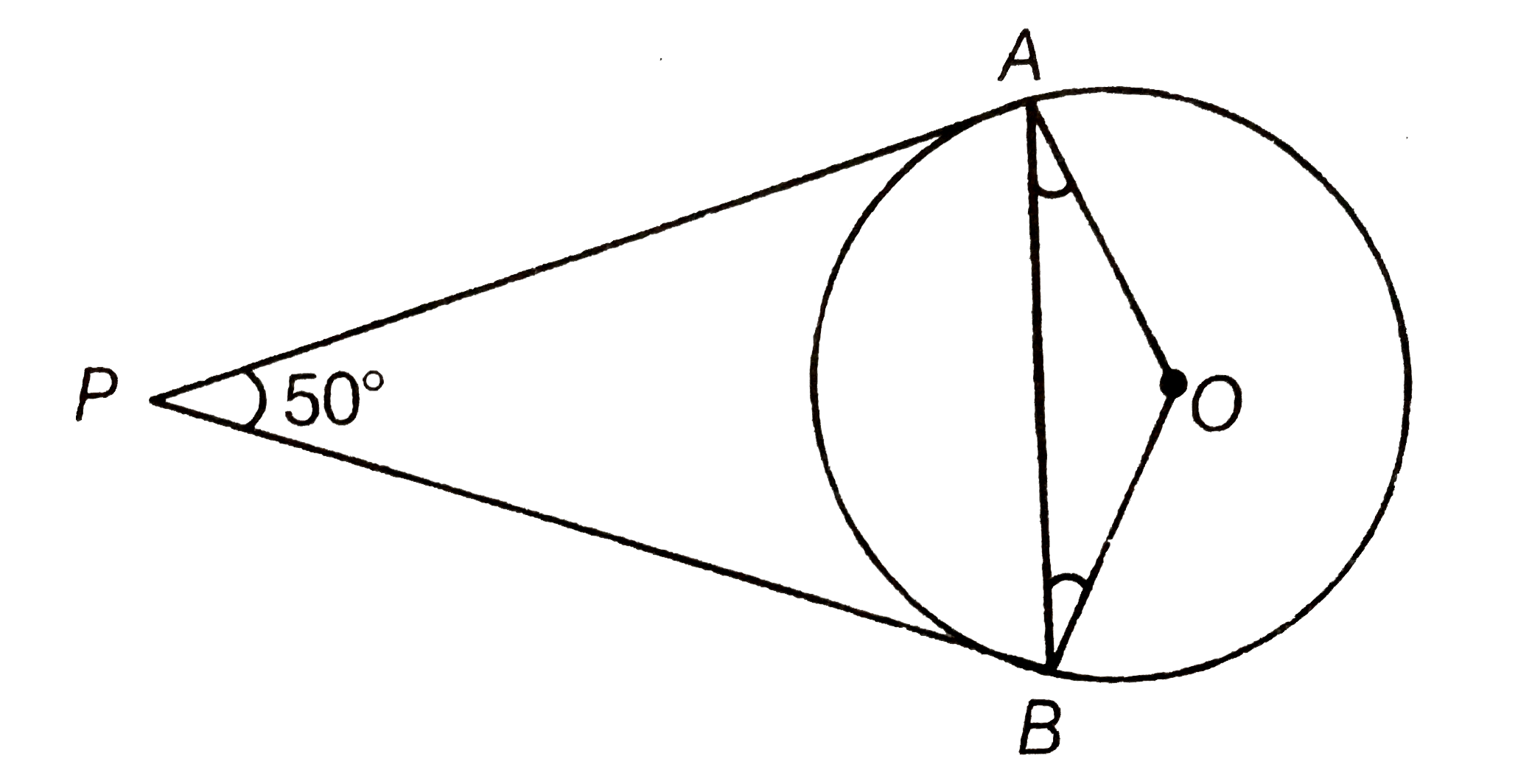
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
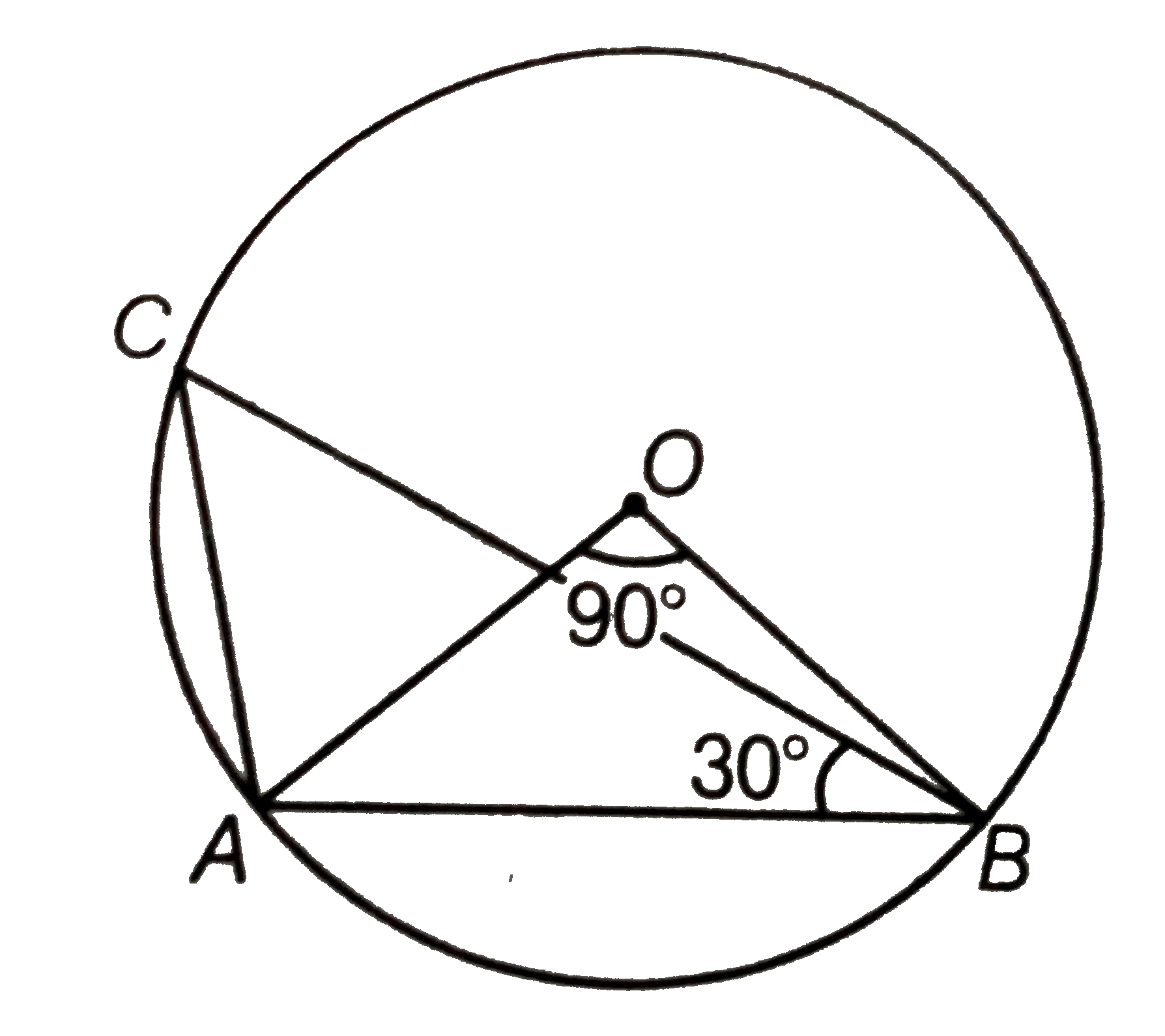
View SolutionIn figure, if ∠AOB=90∘and∠ABC=30∘, then∠CAO is equal to
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
View SolutionIn figure, ∠OAB=30∘and∠OCB=57∘. Find ∠BOCand∠AOC.
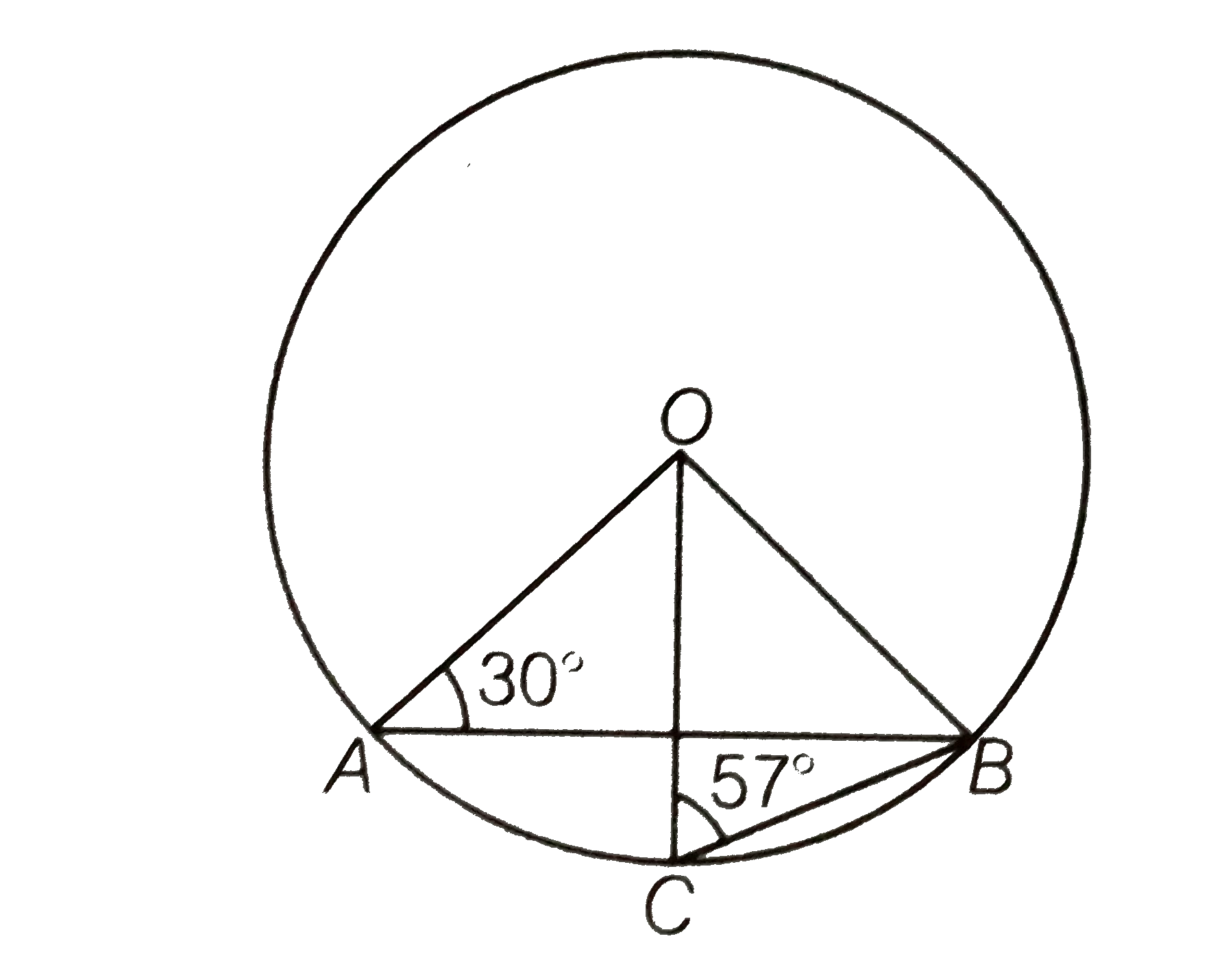
View SolutionIn the given figure, ∠OAB=30∘and∠OCB=57∘, find ∠BOCand∠AOC

View Solution

