AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
To prove that 4q2=p2+3r2 given that AB=2AC and p and q are the distances from the center O to the chords AB and AC respectively, we will follow these steps:
Step 1: Draw the Circle and Chords
1. Draw a circle with center O and radius r.
2. Draw two chords AB and AC such that AB=2AC.
3. Let AC=2a (hence AB=4a) for some length a.
4. Let p be the distance from O to chord AB and q be the distance from O to chord AC.
Step 2: Use the Perpendicular Bisector Theorem
1. Draw perpendiculars from the center O to both chords AB and AC. Let these perpendiculars meet AB at point P and AC at point Q.
2. By the property of chords, AP=PB and AQ=QC.
3. Since AB=4a, we have AP=PB=2a.
4. Since AC=2a, we have AQ=QC=a.
Step 3: Apply the Pythagorean Theorem
1. In triangle OAP:
OA2=OP2+AP2
Substituting the known values:
r2=p2+(2a)2(1)
This simplifies to:
r2=p2+4a2
2. In triangle OAQ:
OA2=OQ2+AQ2
Substituting the known values:
r2=q2+a2(2)
Step 4: Relate the Two Equations
1. From equation (1):
p2=r2−4a2(3)
2. From equation (2):
a2=r2−q2(4)
Step 5: Substitute Equation (4) into Equation (3)
1. Substitute a2 from equation (4) into equation (3):
p2=r2−4(r2−q2)
Simplifying gives:
p2=r2−4r2+4q2
p2=−3r2+4q2
Rearranging gives:
4q2=p2+3r2
Conclusion
Thus, we have proved that:
4q2=p2+3r2
1. Draw a circle with center O and radius r.
2. Draw two chords AB and AC such that AB=2AC.
3. Let AC=2a (hence AB=4a) for some length a.
4. Let p be the distance from O to chord AB and q be the distance from O to chord AC.
1. Draw perpendiculars from the center O to both chords AB and AC. Let these perpendiculars meet AB at point P and AC at point Q.
2. By the property of chords, AP=PB and AQ=QC.
3. Since AB=4a, we have AP=PB=2a.
4. Since AC=2a, we have AQ=QC=a.
1. In triangle OAP:
OA2=OP2+AP2
Substituting the known values:
r2=p2+(2a)2(1)
This simplifies to:
r2=p2+4a2
OA2=OQ2+AQ2
Substituting the known values:
r2=q2+a2(2)
1. From equation (1):
p2=r2−4a2(3)
a2=r2−q2(4)
1. Substitute a2 from equation (4) into equation (3):
p2=r2−4(r2−q2)
Simplifying gives:
p2=r2−4r2+4q2
p2=−3r2+4q2
Rearranging gives:
4q2=p2+3r2
Thus, we have proved that:
4q2=p2+3r2
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
AB is a chord of the circle x2+y2=252 .P is a point such that PA = 4, PB = 3. If AB = 5, then distance of P from origin can be:
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionIn a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
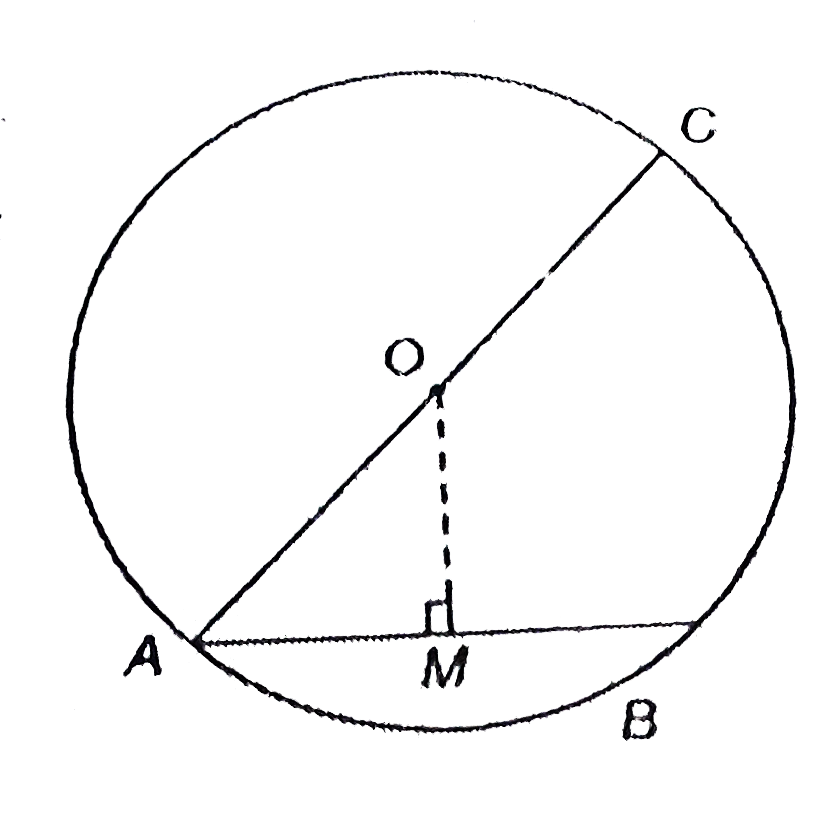
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View Solutionif p:q::r, prove that p:r=p2:q2.
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View Solution
