Before the neutrino hypothesis the beta decay process was throught to be the transition.
If this was true show that if the neutron was at rest the proton and electron would emerge with fixed energies and calculate them. Experimentally the electron energy was found to have a large range.
To solve the problem, we will analyze the beta decay process where a neutron decays into a proton and an electron (beta particle). We will show that if the neutron is at rest, the proton and electron would emerge with fixed energies and calculate those energies.
1. Understanding the Initial Conditions:
- The neutron is at rest, which means its initial momentum Pn is zero.
- The rest mass energy of the neutron is given by En=mnc2, where mn is the mass of the neutron and c is the speed of light.
2. Conservation of Momentum:
- According to the conservation of momentum, the total momentum before the decay must equal the total momentum after the decay.
- Since the neutron is at rest, we have:
Pn=Pp+Pe=0
- Therefore, the momentum of the proton Pp and the momentum of the electron Pe must be equal in magnitude and opposite in direction:
Pp=−Pe
3. Conservation of Energy:
- The total energy before the decay (rest mass energy of the neutron) must equal the total energy after the decay (rest mass energies of the proton and electron plus their kinetic energies).
- Thus, we can write:
En=Ep+Ee
- Where Ep and Ee are the total energies of the proton and electron, respectively.
4. Energy Expressions:
- The total energy of the proton and electron can be expressed using their rest mass energies and their momenta:
Ep=√(mpc2)2+(Ppc)2
Ee=√(mec2)2+(Pec)2
- Here, mp and me are the rest masses of the proton and electron.
5. Substituting into the Energy Conservation Equation:
- Substitute the expressions for Ep and Ee into the conservation of energy equation:
mnc2=√(mpc2)2+(Ppc)2+√(mec2)2+(Pec)2
6. Calculating the Energies:
- The rest mass energies are approximately:
- mnc2≈938MeV
- mpc2≈936MeV
- mec2≈0.51MeV
- The difference in rest mass energy between the neutron and the proton is:
mnc2−mpc2≈938MeV−936MeV=2MeV
- This energy must be shared as kinetic energy between the proton and electron.
7. Final Energies:
- If we assume the proton takes most of the energy due to its larger mass, we can approximate:
Ep≈mpc2+kinetic energy
Ee≈mec2+kinetic energy
- The kinetic energy can be distributed, but the total energy must equal the rest mass energy of the neutron.
Conclusion:
If the neutron is at rest, the proton and electron would emerge with fixed energies that depend on the conservation of momentum and energy. The calculations show that the energies of the proton and electron are related to their rest mass energies and the energy difference due to the decay process.
- The neutron is at rest, which means its initial momentum Pn is zero.
- The rest mass energy of the neutron is given by En=mnc2, where mn is the mass of the neutron and c is the speed of light.
- According to the conservation of momentum, the total momentum before the decay must equal the total momentum after the decay.
- Since the neutron is at rest, we have:
Pn=Pp+Pe=0
- Therefore, the momentum of the proton Pp and the momentum of the electron Pe must be equal in magnitude and opposite in direction:
Pp=−Pe
- The total energy before the decay (rest mass energy of the neutron) must equal the total energy after the decay (rest mass energies of the proton and electron plus their kinetic energies).
- Thus, we can write:
En=Ep+Ee
- Where Ep and Ee are the total energies of the proton and electron, respectively.
- The total energy of the proton and electron can be expressed using their rest mass energies and their momenta:
Ep=√(mpc2)2+(Ppc)2
Ee=√(mec2)2+(Pec)2
- Here, mp and me are the rest masses of the proton and electron.
- Substitute the expressions for Ep and Ee into the conservation of energy equation:
mnc2=√(mpc2)2+(Ppc)2+√(mec2)2+(Pec)2
- The rest mass energies are approximately:
- mnc2≈938MeV
- mpc2≈936MeV
- mec2≈0.51MeV
- The difference in rest mass energy between the neutron and the proton is:
mnc2−mpc2≈938MeV−936MeV=2MeV
- This energy must be shared as kinetic energy between the proton and electron.
- If we assume the proton takes most of the energy due to its larger mass, we can approximate:
Ep≈mpc2+kinetic energy
Ee≈mec2+kinetic energy
- The kinetic energy can be distributed, but the total energy must equal the rest mass energy of the neutron.
If the neutron is at rest, the proton and electron would emerge with fixed energies that depend on the conservation of momentum and energy. The calculations show that the energies of the proton and electron are related to their rest mass energies and the energy difference due to the decay process.
Topper's Solved these Questions
Similar Questions
The β−decay process , discovered around 1900 , is basically the decay of a neutron n. In the laboratory , a proton p and an electron e¯ are observed as the decay product of neutron. Therefore considering the decay of neutron as a two- body decay process, it was predicted theoretically that the kinetic energy of the electron should be a constant . But experimentally , it was observed that the electron kinetic energy has continuous spectrum Considering a three- body decay process , i.e.
n→p+e¯+¯νe, around 1930 , Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (¯νe) to be massaless and possessing negligible energy , and the neutrino to be at rest , momentum and energy conservation principle are applied. From this calculation , the maximum kinetic energy of the electron is 0.8×106eV The kinetic energy carried by the proton is only the recoil energy.
What is the maximum energy of the anti-neutrino ?
View SolutionThe β−decay process , discovered around 1900 , is basically the decay of a neutron n. In the laboratory , a proton p and an electron e¯ are observed as the decay product of neutron. Therefore considering the decay of neutron as a two- body decay process, it was predicted theoretically that the kinetic energy of the electron should be a constant . But experimentally , it was observed that the electron kinetic energy has continuous spectrum Considering a three- body decay process , i.e.
n→p+e¯+¯νe, around 1930 , Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (¯νe) to be massaless and possessing negligible energy , and the neutrino to be at rest , momentum and energy conservation principle are applied. From this calculation , the maximum kinetic energy of the electron is 0.8×106eV The kinetic energy carried by the proton is only the recoil energy.
If the - neutrono had a mass of 3eV/c2 (where c is the speed of light ) insend of zero mass , what should be the range of the kinectic energy K. of the electron ?
View SolutionConsider the decay of a free neutron at rest: n⊤+e− Show that the tow-body dacay of this type must necessarily give an electron of fixed energy and, therefore, cannot for the observed continous energy distribution in the β-decay of a neutron or a nucleus.
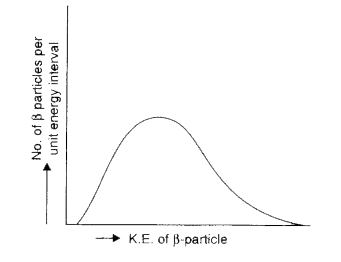
View SolutionA metal foil is at a certain distance from an isotropic point source that emits energy at the rate P. Let us assume the classical physics to be applicable. The incident light energy will be absorbed continuously and smoothly. The electrons present in the foil soak up the energy incident on them. For simplicity , we can assume that the energy incident on a circular path of the foil with radius 5×10−11m (about that of a typical atom ) is absorbed by a single electron. The electron absorbs sufficient energy to break through the binding forces and comes out from the foil. By knowing the work function, we can calculate the time taken by an electron to come out i.e., we can find out the time taken by photoelectric emission to start. As you will see in the following questions, the time decay comes out to be large, which is not practically observed. The time lag is very small. Apparently, the electron does not have to soak up energy . It absorbs energy all at once in a single photon electron interaction.
If power of the source P is 1.5 W and distance of the foil from the source is 3.5 m, the energy received by an electron per second is
View SolutionA metal foil is at a certain distance from an isotropic point source that emits energy at the rate P. Let us assume the classical physics to be applicable. The incident light energy will be absorbed continuously and smoothly. The electrons present in the foil soak up the energy incident on them. For simplicity , we can assume that the energy incident on a circular path of the foil with radius 5×10−11m (about that of a typical atom ) is absorbed by a single electron. The electron absorbs sufficient energy to break through the binding forces and comes out from the foil. By knowing the work function, we can calculate the time taken by an electron to come out i.e., we can find out the time taken by photoelectric emission to start. As you will see in the following questions, the time decay comes out to be large, which is not practically observed. The time lag is very small. Apparently, the electron does not have to soak up energy . It absorbs energy all at once in a single photon electron interaction.
if work function of the metal of the foil is 2.2 eV, the time taken by electron to come out is nearly
View SolutionA metal foil is at a certain distance from an isotropic point source that emits energy at the rate P. Let us assume the classical physics to be applicable. The incident light energy will be absorbed continuously and smoothly. The electrons present in the foil soak up the energy incident on them. For simplicity , we can assume that the energy incident on a circular path of the foil with radius 5×10−11m (about that of a typical atom ) is absorbed by a single electron. The electron absorbs sufficient energy to break through the binding forces and comes out from the foil. By knowing the work function, we can calculate the time taken by an electron to come out i.e., we can find out the time taken by photoelectric emission to start. As you will see in the following questions, the time decay comes out to be large, which is not practically observed. The time lag is very small. Apparently, the electron does not have to soak up energy . It absorbs energy all at once in a single photon electron interaction.
The experimental observations show that the waiting time for emission is 10−8 s. This observation contradicts the calculations based on classical physics view of light energy . Thus we have to assume that during photoelectron emission
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to n(n−1)2If teh electron comes back from the energy level having energy E2 to the energy level having energy E1 then the difference may be expresent in terms of energy of photon as E2−E1=ΔE,λ=hc/ΔE Since h and c are constants ΔE coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula ¯v=RZ2(1n21−1n212)Where R is a Rydherg constant
Its a single isolated atom, an electrons make transition from fifth excited state is second thern maximum number of different type of photon observed is
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to n(n−1)2If teh electron comes back from the energy level having energy E2 to the energy level having energy E1 then the difference may be expresent in terms of energy of photon as E2−E1=ΔE,λ=hc/ΔE Since h and c are constants ΔE coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula ¯v=RZ2(1n21−1n212)Where R is a Rydherg constant
The wave number of electromagnetic radiation emitted during the transition of electron in between the two levels of Li2+ ion whose pricipal quantum numbner sum is 4 and difference is 2 is
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to n(n−1)2If teh electron comes back from the energy level having energy E2 to the energy level having energy E1 then the difference may be expresent in terms of energy of photon as E2−E1=ΔE,λ=hc/ΔE Since h and c are constants ΔE coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula ¯v=RZ2(1n21−1n212)Where R is a Rydherg constant
If the ionisation potential for hydrogen -like atom in a sample is 122.4V then the series limit of the paschen series for this atom is
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to n(n−1)2If teh electron comes back from the energy level having energy E2 to the energy level having energy E1 then the difference may be expresent in terms of energy of photon as E2−E1=ΔE,λ=hc/ΔE Since h and c are constants ΔE coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula ¯v=RZ2(1n21−1n212)Where R is a Rydherg constant
The difference in the wavelength of the second line is Lyman series and last line of breaker series is a hydrogen sample is
View Solution
