A nuclide 1 is said to be the mirror isobar of nuclide 2 if Z1=N1 and Z2=N1. (a) What nuclide is a mirror isobar of 23.11 Na ? (b) which nuclide out of the two mirror isobars have greater binding energy and why?
To solve the problem, we will break it down into two parts as given in the question.
Part (a): Finding the mirror isobar of 23Na11
1. Identify the atomic number and mass number of sodium (Na):
- The atomic number Z1 of sodium is 11 (this represents the number of protons).
- The mass number A1 of sodium is 23.
2. Calculate the number of neutrons in sodium:
N1=A1−Z1=23−11=12
So, for sodium, we have:
- Z1=11
- N1=12
3. Determine the properties of the mirror isobar:
- For the mirror isobar, we need to find a nuclide where:
- Z2=N1=12
- N2=Z1=11
4. Identify the nuclide with Z2=12:
- The nuclide with atomic number 12 is magnesium (Mg).
5. Calculate the mass number of magnesium:
A2=Z2+N2=12+11=23
Thus, the mirror isobar of sodium 23Na11 is 23Mg12.
Part (b): Comparing the binding energy of the two mirror isobars
1. Identify the two nuclides:
- The two nuclides are:
- Sodium 23Na11
- Magnesium 23Mg12
2. Compare the number of protons:
- Sodium has 11 protons, while magnesium has 12 protons.
3. Understand the relationship between binding energy and the number of protons:
- Generally, nuclides with a higher number of protons tend to have greater binding energy due to the stronger nuclear force that holds the nucleus together.
4. Conclusion:
- Since magnesium has more protons than sodium, it will have a greater binding energy.
Final Answers:
(a) The mirror isobar of 23Na11 is 23Mg12.
(b) Magnesium has greater binding energy because it has more protons.
---
- The atomic number Z1 of sodium is 11 (this represents the number of protons).
- The mass number A1 of sodium is 23.
N1=A1−Z1=23−11=12
So, for sodium, we have:
- Z1=11
- N1=12
- For the mirror isobar, we need to find a nuclide where:
- Z2=N1=12
- N2=Z1=11
- The nuclide with atomic number 12 is magnesium (Mg).
A2=Z2+N2=12+11=23
Thus, the mirror isobar of sodium 23Na11 is 23Mg12.
- The two nuclides are:
- Sodium 23Na11
- Magnesium 23Mg12
- Sodium has 11 protons, while magnesium has 12 protons.
- Generally, nuclides with a higher number of protons tend to have greater binding energy due to the stronger nuclear force that holds the nucleus together.
- Since magnesium has more protons than sodium, it will have a greater binding energy.
(a) The mirror isobar of 23Na11 is 23Mg12.
Topper's Solved these Questions
Similar Questions
The value of cot(23∑n=1cot−1(1+n∑k=12k)) is
View SolutionTwo mirror labelled L1 for left mirror and L2 for right mirror (L2) looks into this mirror and sees a series of images. The second nearest image seen in the right mirror is situated at a distance:
_E01_003_Q01.png)
View SolutionThe sum, 10Σn−1n(2n+1)(2n−1)5 is equal to.........
View SolutionIf z1 is a complex number other than -1 such that |z1|=1 and z2=z1−1z1+1 , then show that the real parts of z2 is zero.
View SolutionNuclei with magic no. of proton Z=2,8,20,28,50,52 and magic no. of neutrons N=2,8,20,28,50,82 and 126 are found to be stable. (i) Verify this by calculating the proton separation energy Sp for .120Sn(Z=50) and .121Sb=(Z=51).
The proton separation energy for a nuclide is the minimum energy required to separated the least tightly bound proton form a nucleus of that nuclide. It is given by
Sp=(Mz−1,N+MH−MZ,N)c2.
given .119Sn49=118.9058u,.120Sn50=119.902199u,.121Sb51=120.903824u,.1H=1.0078252u
(ii) what does the existence of magic number indicate?
View SolutionA convex mirror offocal length fforms an image which is 1/n times the object. The distance of the object from the mirror is:
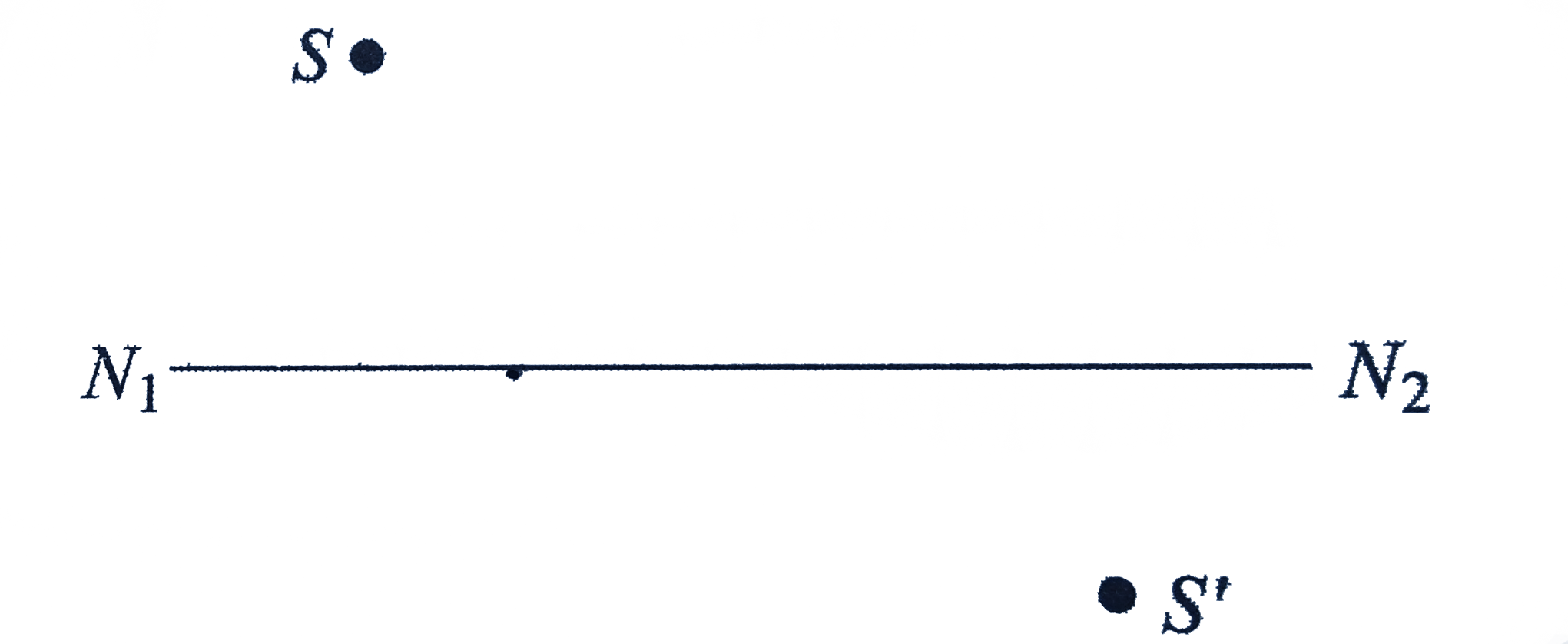
View SolutionPoint S′ is the image of a point source of light S in a spherical mirror whose optical axise is N1N2 (shown in Figure). Find by construction the position of the center of the mirror and its focus.
View SolutionA radio nuclide with half life T=69.31 second emits β-particles of average kinetic energy E=11.25eV. At an instant concentration of β-particles at distance, r=2m from nuclide is n=3×1013 per m3.
(i) Calculate number of nuclei in the nuclide at that instant.
(ii) If a small circular plate is placed at distance r from nuclide such that β-particles strike the plate normally and come to rest, calculate pressure experienced by the plate due to collision of β-particle. (Mass of β-particle =9×10−31kg) (loge2=0.693)
View SolutionA radio nuclide A1 with decay constant λ1 transforms into a radio nuclide A2 with decay constant λ2. Assuming that at the initial moment, the preparation contained only the radio nuclide A1
(a) Find the equation decribing accumulation of radio nuclide A2 with time. (b) Find the time interval after which the activity of radio nuclide A2 reaches its maximum value.
View SolutionA radio nuclide A1 with decay constant λ1 transforms into a radio nuclide A2 with decay constant λ2. Assuming that at the initial moment, the preparation contained only the radio nuclide A1
(a) Find the equation describing accumulation of radio nuclide A2 with time. (b) Find the time interval after which the activity of ratio nucliei A2 reaches its maximum value.
View Solution
