Consider the L-C-R circuit shown in the fiure. Find the net current I and the phase of i. Show that i=VZ. Find the impedance Z of this circuit.

Video Solution
Text Solution
The correct Answer is:A
In the given figure i is the total current from the source. It is divided into two parts, i1 through R and i2 throgh series combination of C and L.
So, we can write i=i1+i2
Vmsinωt=Ri1 (from the circuit diagram)
i1=VmsinωtR.............(i)
If q2 is charge on the capacitor at any time t, then for series combination of C and L.
Applying KVL inthe Lower circuit as shown.

q2C+Ldi2dt−Vmsinωt=0
⇒q2C+Ld2q2(dt)2=Vmsinωt [∴i2=dq2dt]......(ii)
Let q2=qmsin(ωt+ϕ)..............(iii)
dq2dt=qmcos(ωt+ϕ)
⇒d2q2dt2=−qmω2sin(ωt+ϕ)
Now putting the values in Eq. (ii), we get
qm[1C+l(−ω2)]sin(ωt+ϕ)=Vmsinωt
If ϕ=0 and (1C−Lω6(2))>0,
then qm=vm1C−Lω2..............(iv)
From Eq. (iii), i2=dq2dt=ωqmcos(ωt+ϕ)
Using Eq. (iv), i2=ωVmcos(ωt+ϕ)1C−Lω2
Taking ϕ=0,i2=Vmcos(ωt)1ωC−Lω
From Eqs. (i) and (v), we find that i1 and i2 are out of phase by ϕ2
Now, i1+i2=VmsinωtR+Vmcosωt1ωC−Lω
Put VmR=A=Ccosϕ and Vm1ωC−Lω=B=Csinϕ
∴i1+i2=Ccosϕsinωt+Csinϕcosωt
=C=√A2+B2
and ϕ=tan−1BAC=⎡⎣V2mR2+V2m1ωC−Lω⎤⎦1/2
and ϕ=tan−1=R1ωC−Lω
Hence, i=i1+i2=⎡⎢
⎢
⎢⎣V2mR2+V2m(1ωC−Lω)2⎤⎥
⎥
⎥⎦1/2sin(ωt+ϕ)
or iVm=1Z=⎡⎢
⎢
⎢⎣1R2+1(1ωC−Lω)2⎤⎥
⎥
⎥⎦1/2
This is the expression for impedance Z of the circuit.
|
Topper's Solved these Questions
Similar Questions
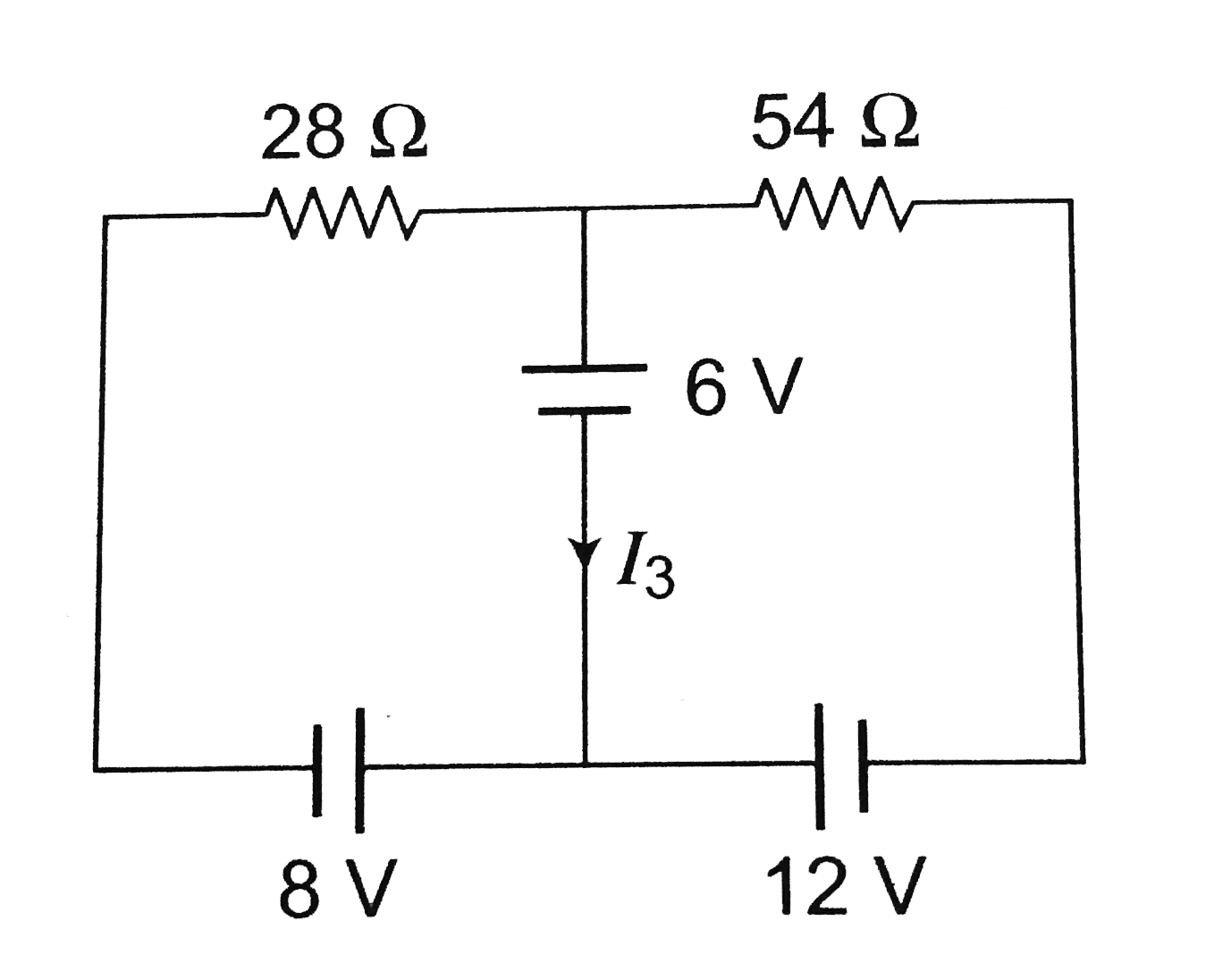
Consider the circuit shown in the figure. The current I3 is equal to
View SolutionIn the circuit shown in the figure
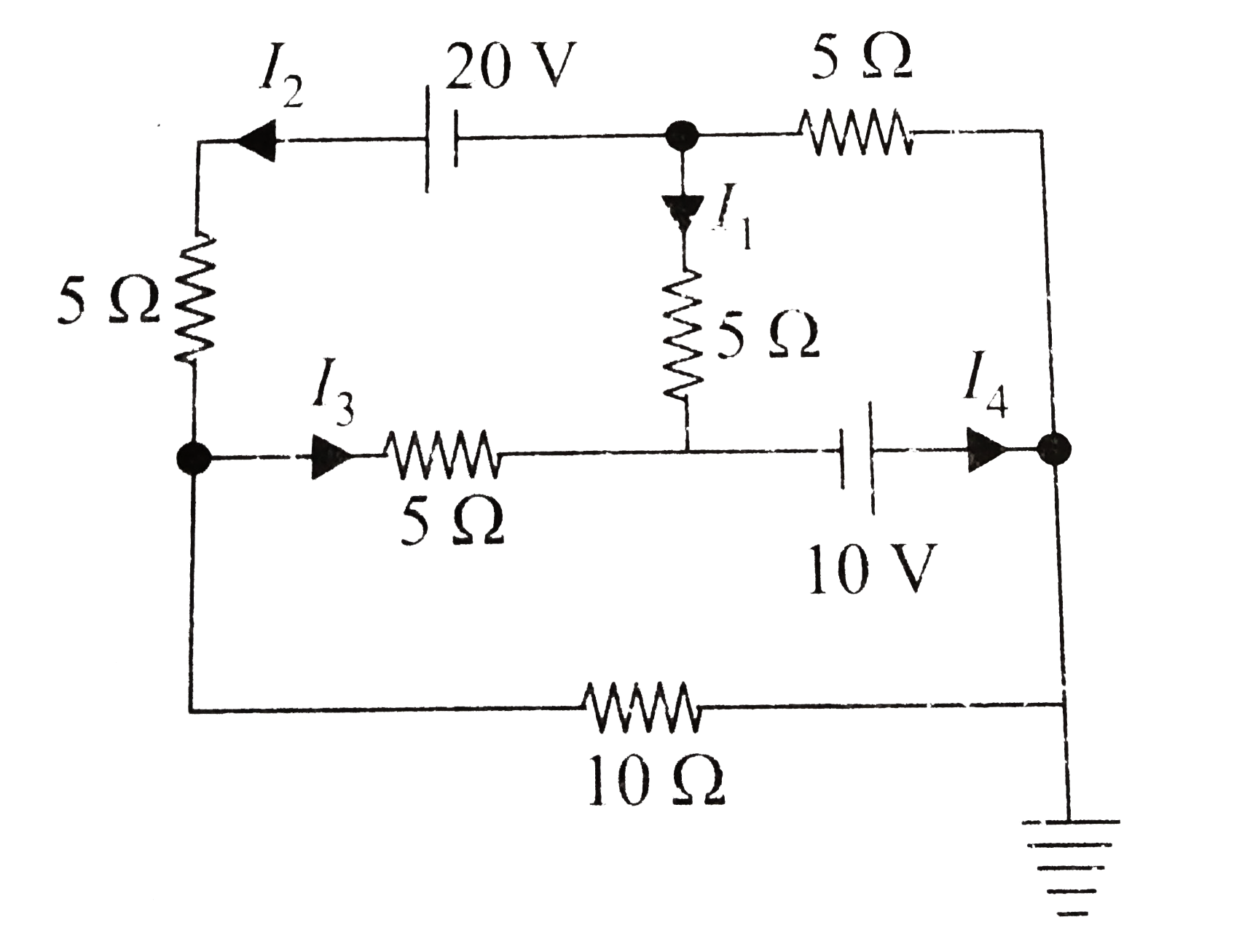 .
.
The value of current I4 is
View SolutionFor the circuit shown in the figure current I will be
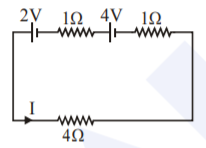
View SolutionFind the current I in the given circuit
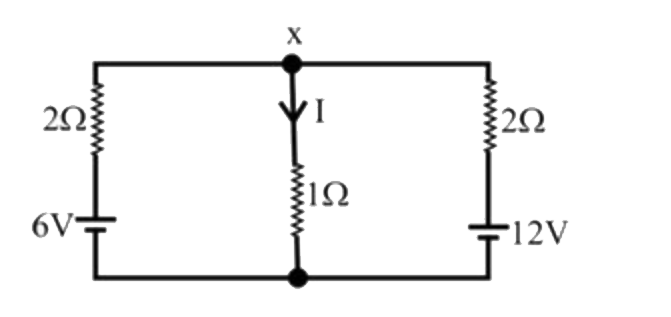
View SolutionIn the circuit shown in figure , find the value of RC.
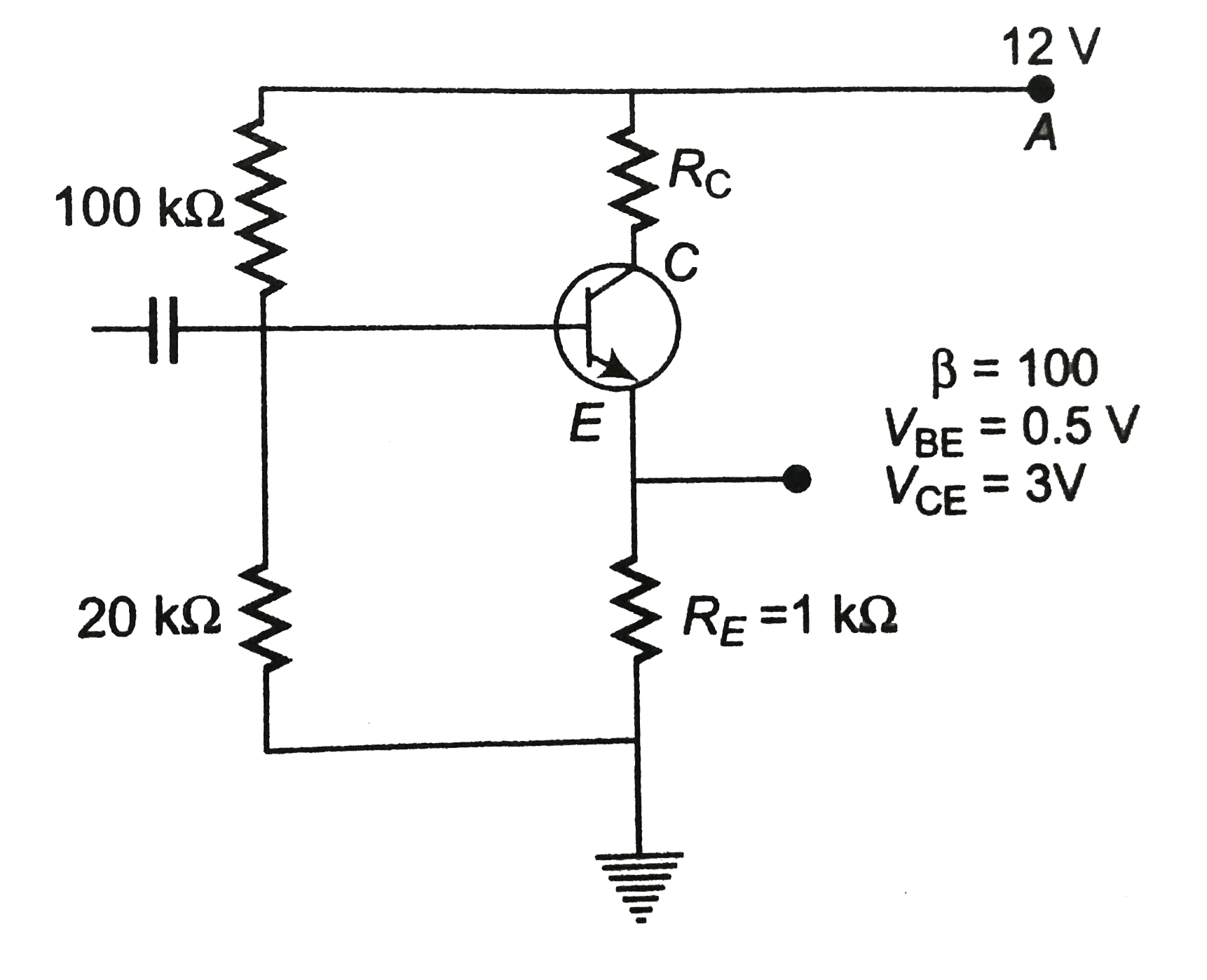
View SolutionIn the circuit shown in the figure,
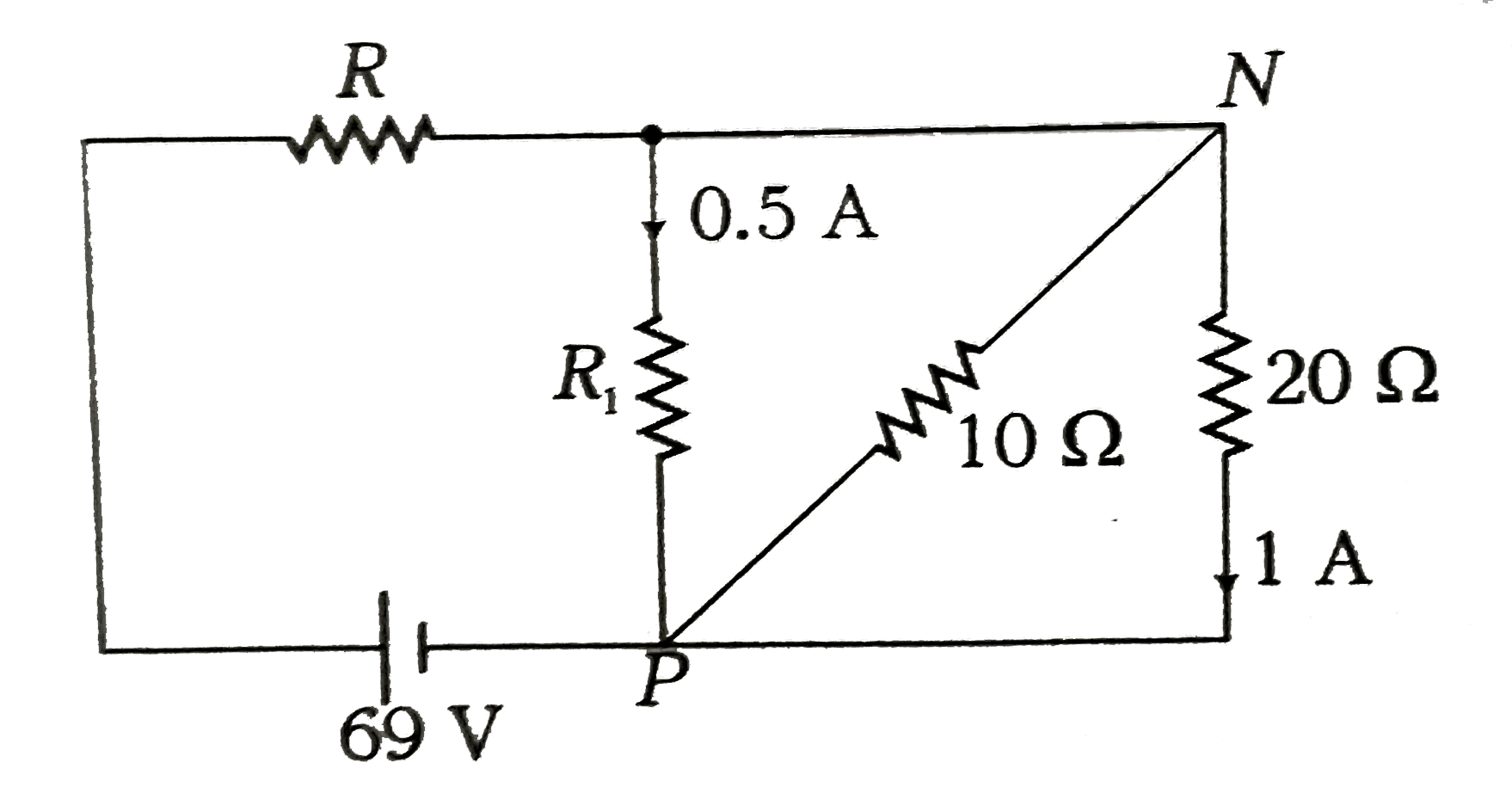
View SolutionIn the circuit shown in figure ,find the ratio of currents i1/i2.

View SolutionIn the circuit as shown in figure, the ratio of current i1/i2 is
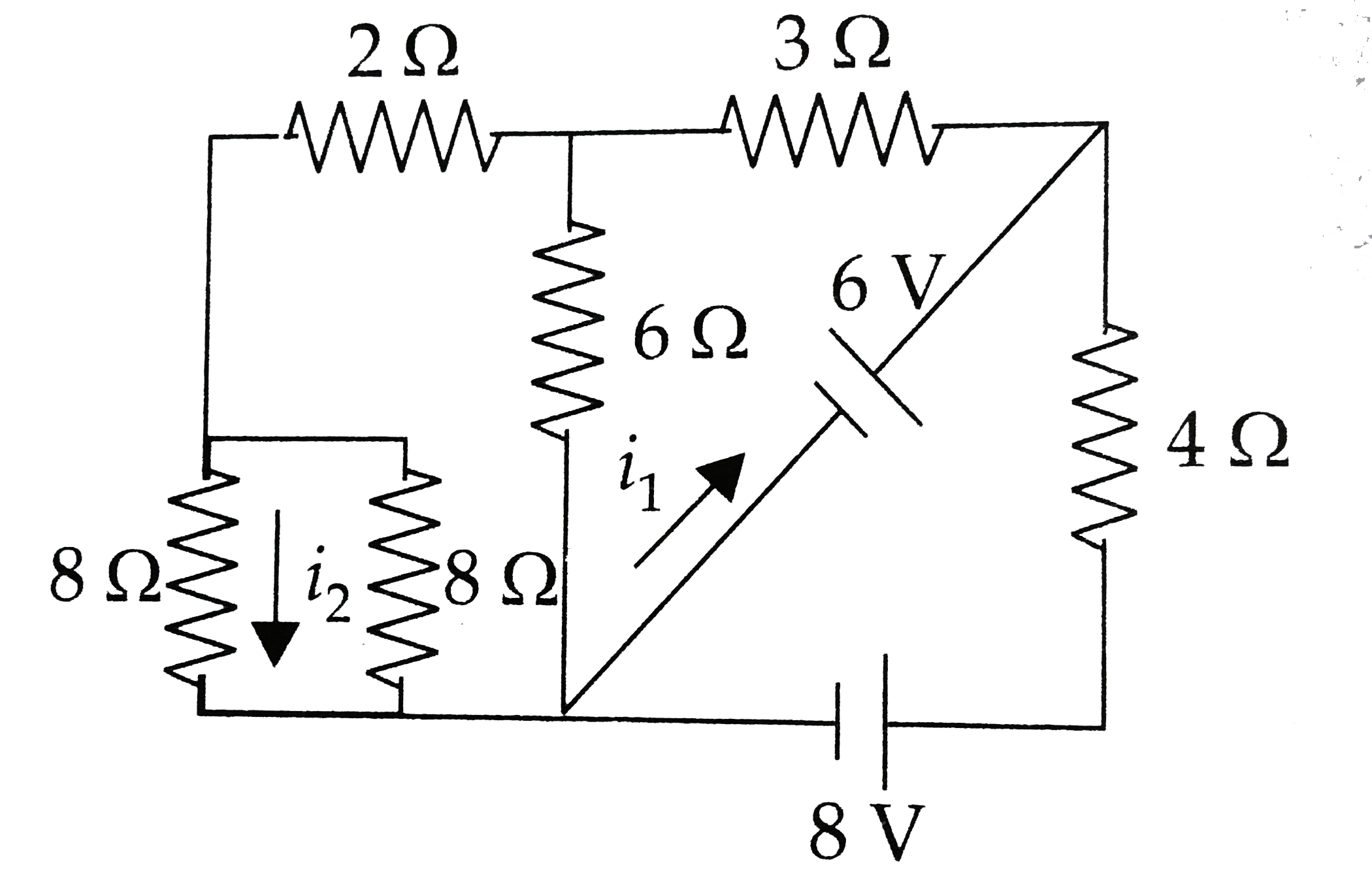
View SolutionIn the circuit shown, the currents i1 and i2 are
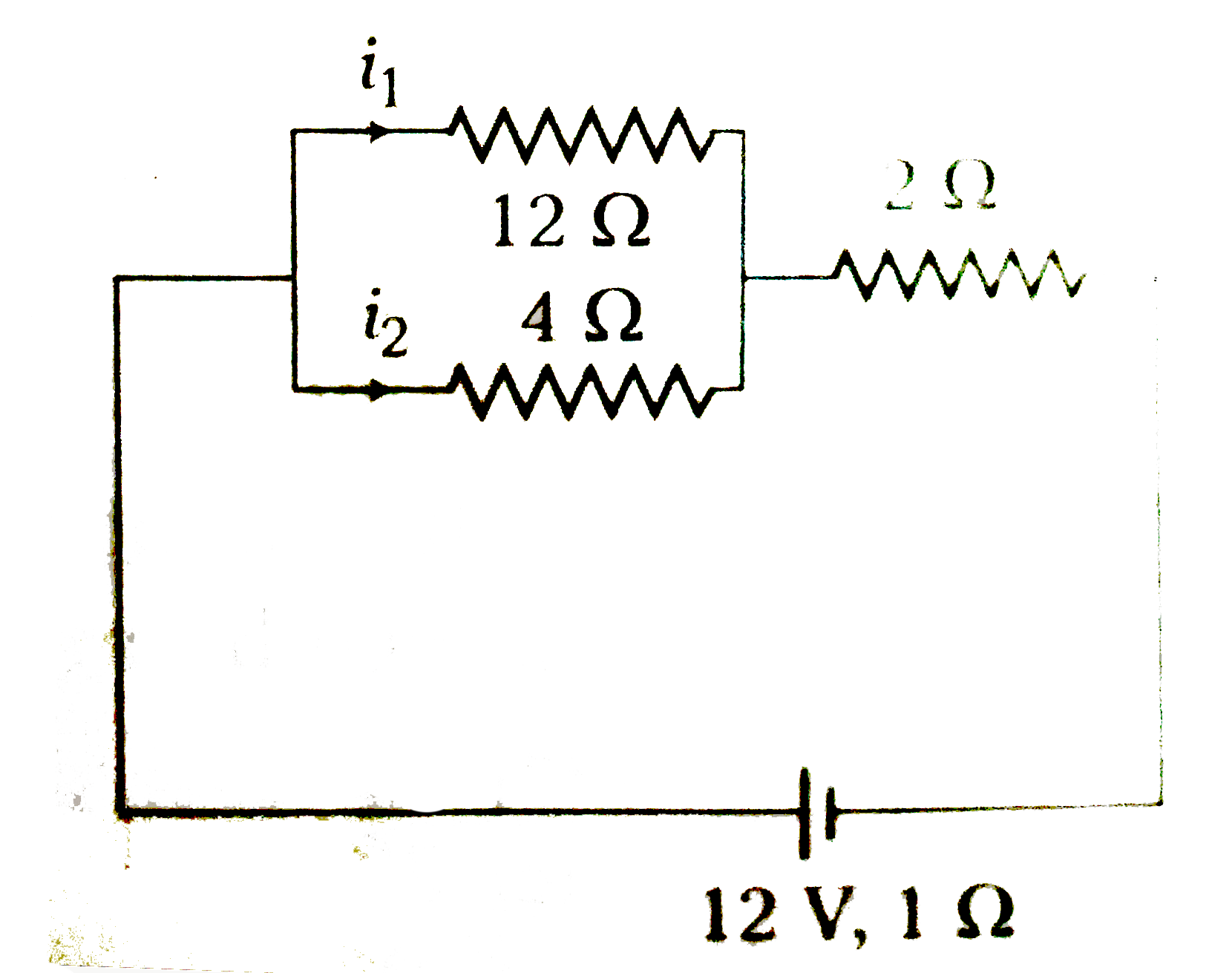
View SolutionConsider the circuit shown in the figure. Find the current in branch AO and OC . Potential of point A = 10 V of point B = 20 V and of C = 30 V.
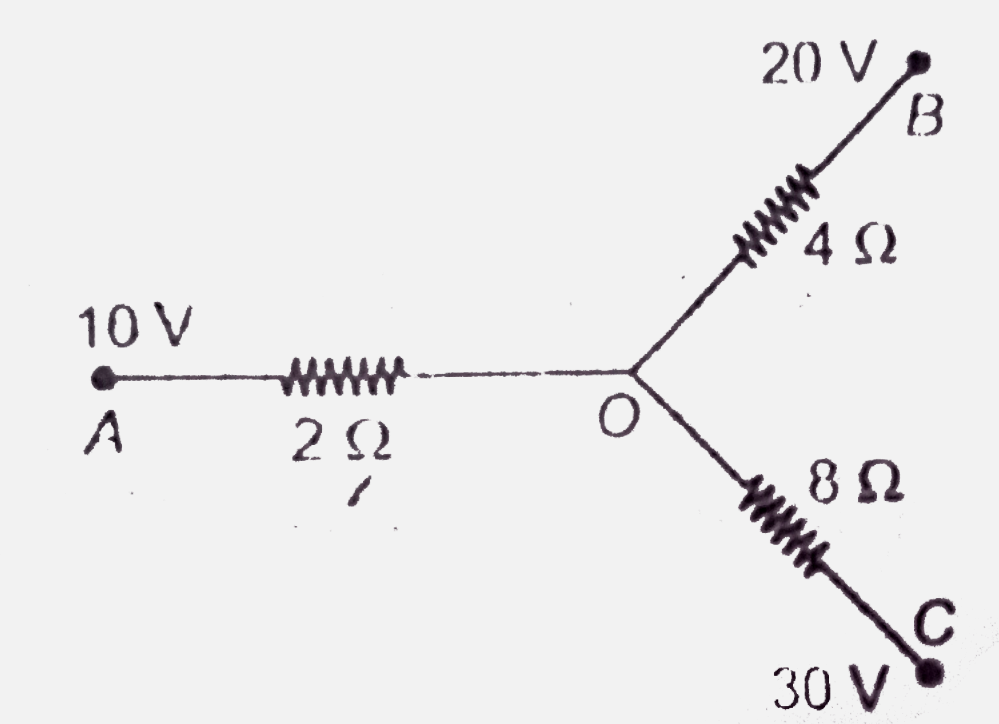
View Solution

