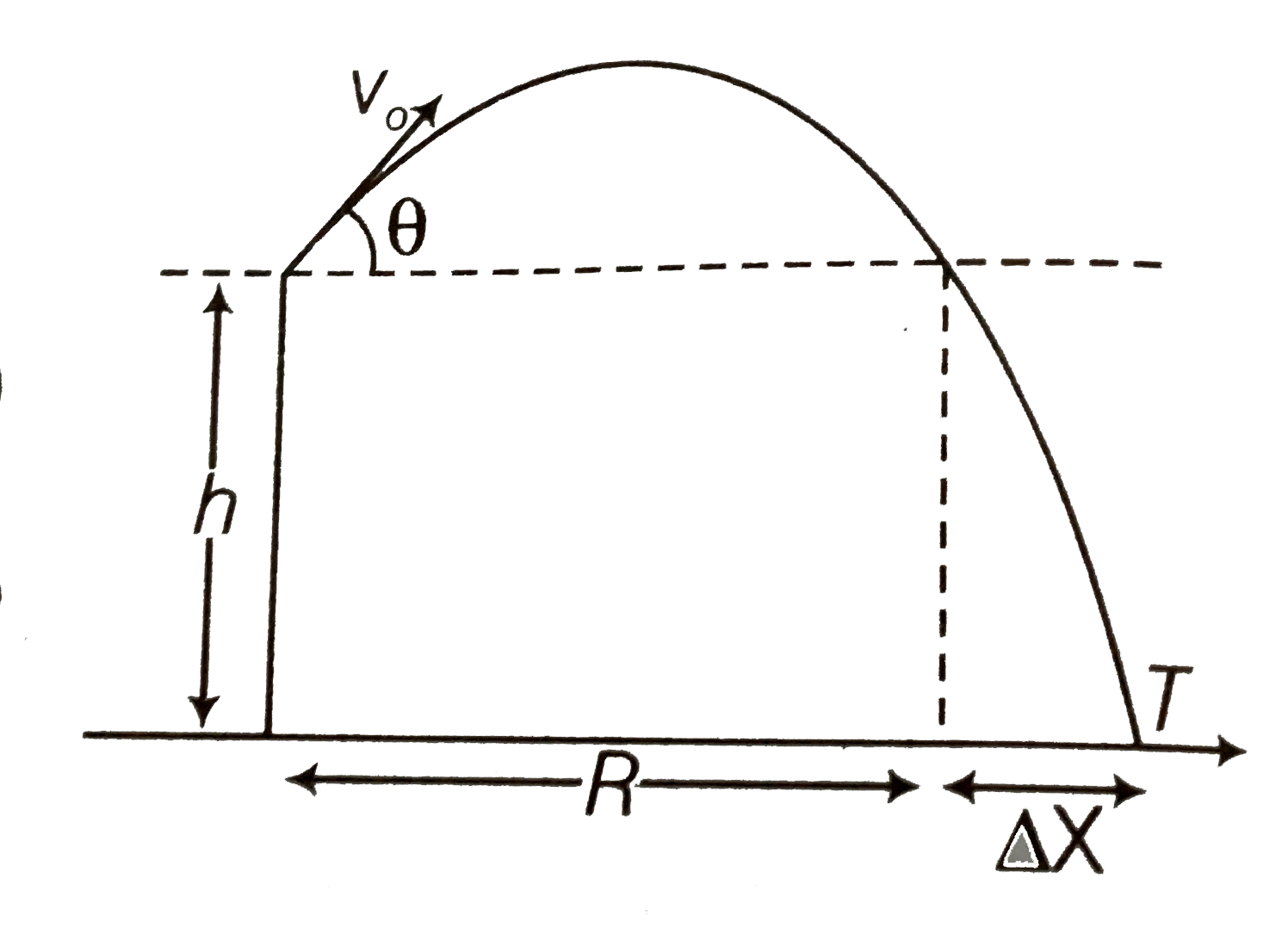
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R=v20g. If a target farther away by distance Δx (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least h=Δx[1+ΔxR]
![A gun can fire shells with maximum speed v(0) and the maximum horizontal range that can be achieved is R=(v(0)^(2))/(g). If a target farther away by distance Deltax (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least h=Delta x[1+(Deltax)/(R)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_NCERT_EXE_PHY_XI_C03_S01_030_Q01.png)
This problem can be approached in two different ways
(i) Refer to the diagram , target T is at horizontal distance x=R+Δx and between point of projection y= -h.
(ii) From point P in the diagram projection at speed v0 at an angle θ below horizontal with height h and horizontal range ΔxA)
Applying method (i)
Maximum horizontal range
R=v20g,forθ=45∘ ...(i)
Let the gun be raised through a height h from the ground so that it can hit the traget. Let vertically downward direction is taken as positive
Horizontal component of initial velocity =v0cosθ
Vertical component of initial velocity =−v0sinθ
Taking motion in vertical direction, h=(−v0sinθ)t=12gt2 ...(ii)
Taking motion in horizontal direction
(R+Δx)=v0cosθ×t
⇒ t=(R+Δx)v0cosθ ...(iii)
Substituting value of t in Eq. (ii) , we get
h=(−v0sinθ)×(R+Δxv0cosθ)+12g(R+Δxv0cosθ)2
h=−(R+Δx)tanθ+12g((R+Δx)2)v20cos2θ
As angle of projection is θ=45∘ , therefore
h=−(R+Δx)+tan45∘+12g.(R+Δx)2v20cos245∘
h=−(R+Δx)×1+12g.(R+Δx)2v20(1/2)
(.∴tan45∘=1andcos45∘=1√2)
h=−(R+Δx)+(R+Δx2)R [Using Eq. (i) , R=v20/g]
=−(R+Δx)+1R(R2+Δx2+2RΔx)
=−R−Δx+(R+Δx2R+2Δx)
=Δx+Δx2R
h=Δx(1+ΔxR)
Topper's Solved these Questions
Similar Questions
An artillary piece which consistently shoots its shells with the same muzzle speed has a maximum range R. To hit a target which is R/2 from the gun and on the same level, the elevation angle of the gun should be
View SolutionIf the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
View Solution
Knowledge Check
A player kicks a ball at a speed of 20ms−1 so that its horizontal range is maximum. Another players 24m away in the direction of kick starts running in the same direction at the same instant of hit. If he has to catch the ball just before it reaches the ground, he should run with a velocity equal to (takeg=10ms−2)
A2√2ms−1B4√2ms−1C6√2ms−1D10√2ms−1
If the range of a gun which fires a shell with muzzle speed V is R , then the angle of elevation of the gun is
View SolutionTwo guns A and B can fire bullets at speeds 1 km/s and 2 km/s respectively. From a point on a horizontal ground, they ared fired in all possible directions. The ratio of maximum areas covered by the bullets fired by the two guns, on the ground is :
View SolutionA body projected horizontally with a velocityv from a height h has a range R.With what velocity a body is to be projected horizontally from a height h/2 to have the same range ?
View SolutionA cannon on a level plane is aimed at an angle α above the horizontal and a shell is fired with a muzzle velocity v0 towards a vertical cliff a distance R away. Then the height from the bottom at which the shell strikes the side walls of the cliff is
View SolutionAn aeroplane flies horizontally at a height h at speed v. An anti - carft gun a shell at the plane when it is vertically above the gun . Show that the minimum muzzle velocity required to hit the plane is √v2+2gh at an angle tan−1(√2ghv) .
View SolutionA gun of mass m1 fires a bullet of mass m2 with a horizontal speed
v0. The gun is fitted with a concave mirror of focal length f facing towards a
receding bullet.Find the speed of separations of the bullet and the image just after the gun was fired.
View SolutionA rocket starts vertically upward with speed v0. Show that its speed v at height h is given by v20−v2=2hg1+hR
where R is the radius of the earth and g is acceleration due to gravity at earth's suface. Deduce an expression for maximum height reachhed by a rocket fired with speed 0.9 times the escape velocity.
View Solution