A double slit experiment is performed with light of wavelength 500 nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will ......Solution in Gujrati
remain unshifted.
shift downward by nearly two fringes.
shift upward by nearly two fringes.
shift downward by 10 fringes
The correct Answer is:C
Path difference produced due to film,
Δx=μt−t
=(ν−1)t
=(1.5−1)×2×10−6
=1μm
Now Δx=ydDy=Δxd
y=Dd×1μm
Width of fringe W=dλd
=Dd×500×10−9m
=Dd×0.5×1μm
∴y=Dd×1μm
=2×Dd×12×1μ=2W
Hence, the central fringe will shift upward by nearly two fringes.
Topper's Solved these Questions
- WAVE OPTICSBOOK - KUMAR PRAKASHANCHAPTER - WAVE OPTICSEXERCISE - SECTION-C NCERT Exemplar Solution (Long Answer Type Questions)
5 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS BOOK - KUMAR PRAKASHANCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS EXERCISE - Section-D : Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams)
129 Videos
Similar Questions
if the intensity of the principal maximum in the single slit Fraunhoffer diffraction pattern, then the intensity when the slit width is double will be .....
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
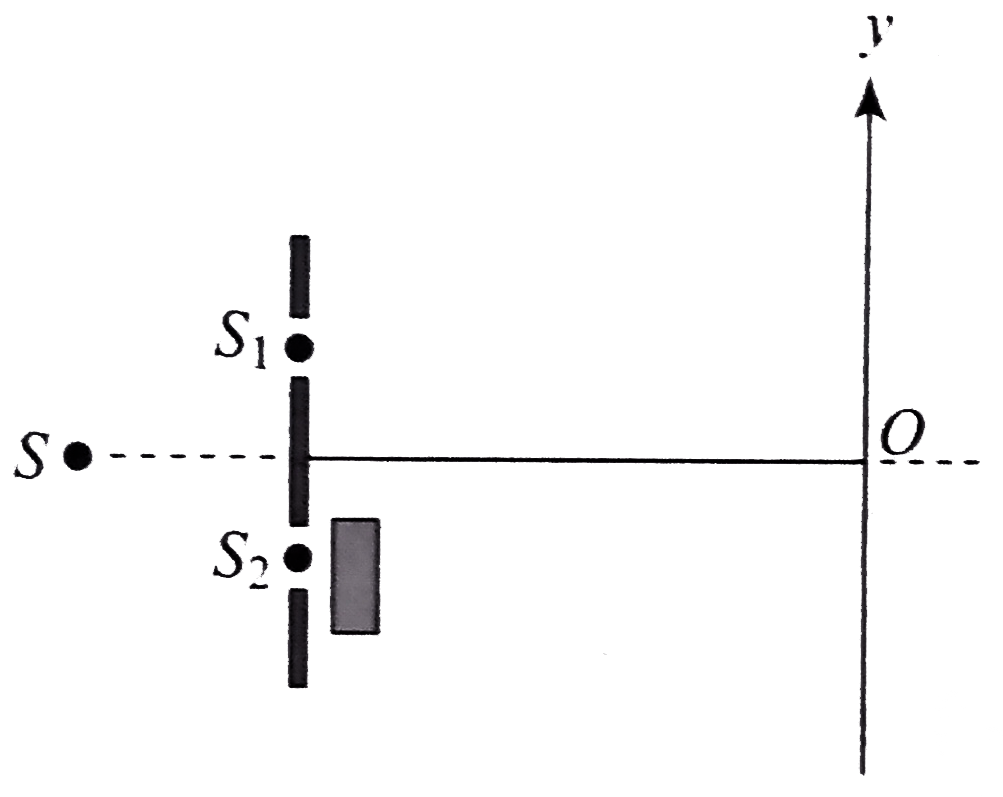
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionIn the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength lambda ), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionA thin sheet of glass (refractive index 1.5) of thickness 6 microns, introduced in the path of one of the interfering beams in a double-slit experiment shift the central fringe to a position earlier occupied by the fifth bright fringe. The wavelength of light used is
View SolutionOn introducing a thin film in the path of one of the two interfering beam, the central fringe will shift by one fringe width. If μ=1.5, the thickness of the film is (wavelength of monochromatic light is λ)
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View SolutionIn Young's double slit experiment the two slits are illuminated with light of wavelength λ .The thickness of a film of refractive index 1.4 to be introduced in the path of one of the interfering beams so that the central image shifts by one fringe width is
View SolutionThe central fringe shifts to the position of fifth bright fringe, if a thin film of refractive index 1.5 is introduced in the path of light of wavelength 5000Å. The thickness of the glass plate is
View SolutionYoung's double slit experiment is performed with monochromatic light. A thin film is introduced in front of one of the slits
View SolutionOn introducing a thin film in the path of one of the two interfering beam, the central fringe will shift by one fringe width if μ=1.5, the thickness of the film is (wavelength of monochromatic light is λ)
View Solutionएक 500 nm तरंगदैर्ध्य वाले प्रकाश पर द्वि-स्लिट प्रयोग किया जाता है। जब एक 2μn मोटाई की तथा अपवर्तक सूचकांक 1.5 की एक पतली फिल्म ऊपरी बीमा के पथ पर आपतित होती है, तब केन्द्रीय उच्चिष्ठ की स्थिति
View SolutionA thin film of a material of refractive index 1.38 is coated on a glass surface of refractive index 1.5.Light of wavelength 550 nm gives no reflected light. The minimum thickness of the film is :
View SolutionOn introducing a thin film in the path of one of the two interfering beam, the central fringe will shift by one fringe width. If mu=1.5, the thickness of the film is (wavelength of monochromatic light is lambda )
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View SolutionIn the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength λ), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View Solution
