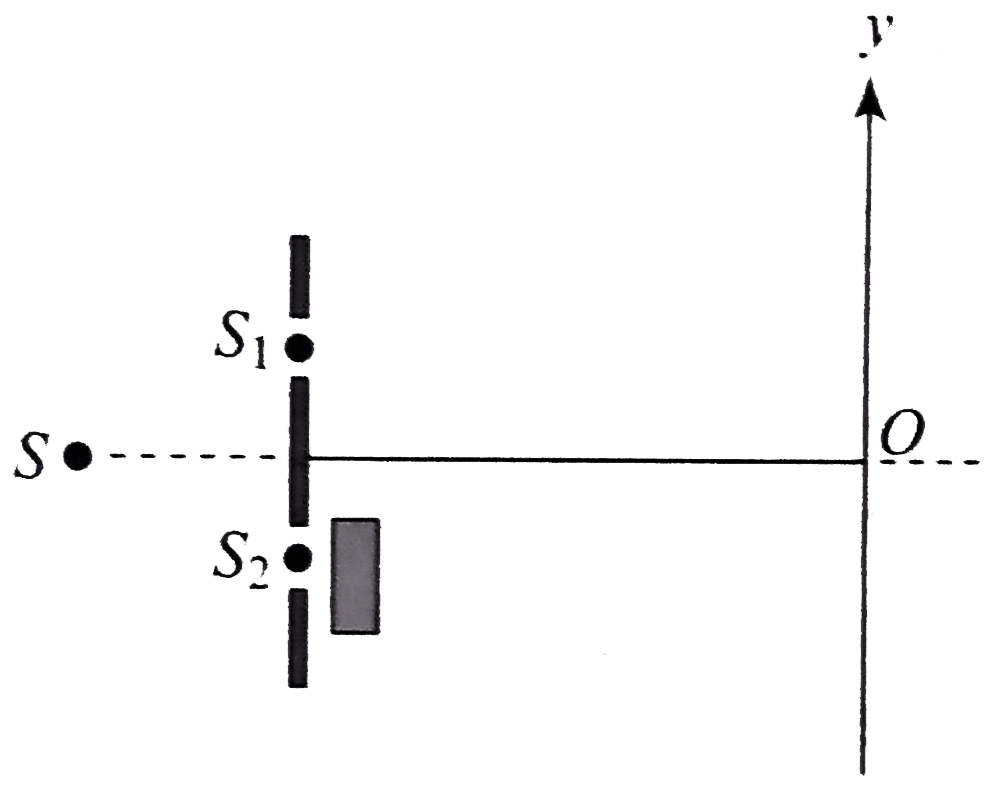
A YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
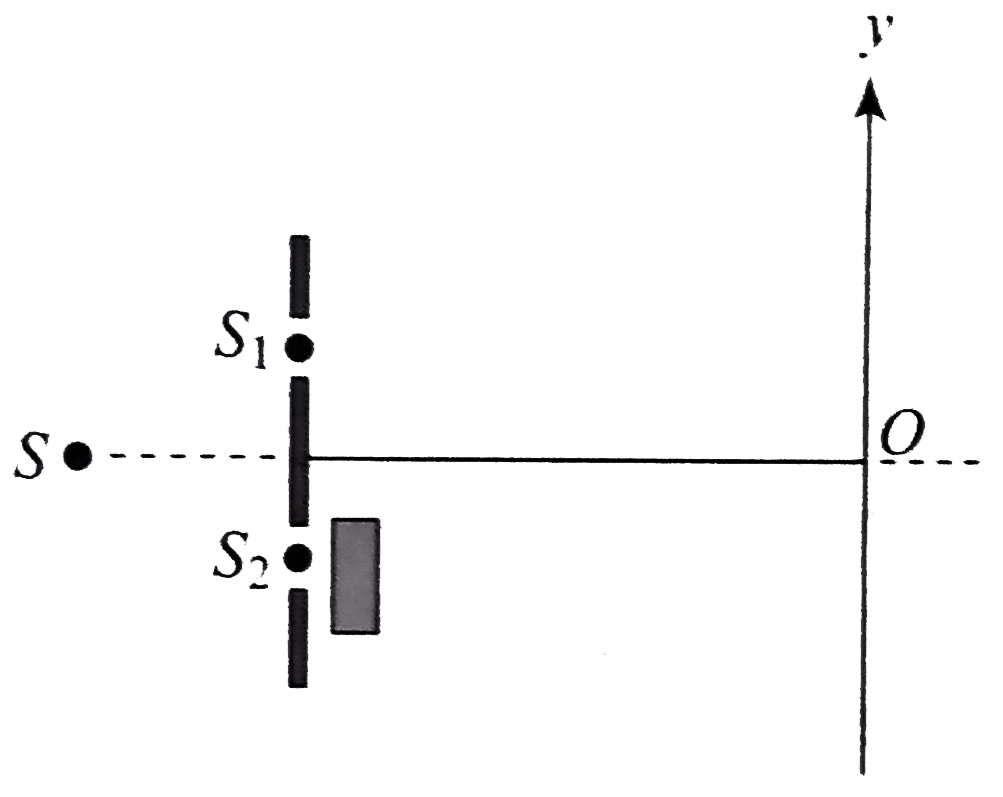
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
2.33 mm
4.33 mm
6.33 mm
4.43 mm
The correct Answer is:d
Path difference at point P on the screen, Δx=ydD
At the position of central maxima, the optical path length S2P and S1P and equal.
(S2P−t)c/μ1=1c/μ2=S1Pc/μ1
where μ1=4/3,μ2=3/2.
μ1(S1P−S2P)=(μ2−μ)t
μ1(ydD)=(μ2−μ1)t
y=(μ2−μ1)tDμ1d
=[(3/2)−(4/3)]×10.4×1.5(4.3)×0.45×10−3=4.33mm

b. At point O, net path difference.
Δx=(μ2μ1−1)t
Net phase difference,
Δϕ=2πλΔx
=2π6×10−7(1.54/3−1)(10.4×10−6)=(133)π
Thus, intensity
I=Imaxcos2(ϕ/2)
=Imaxcos2(13π6)=34Imax
c. For maximum intensity at point O,
Δx=nλ
Path difference at point O,
Δx=(1.54/3−1)(10.4×10−6)=1300nm
Thus, maximum intensity will correspond to 13002nm,
13003nm,...
In the given range, required values are 650 nm and 433.33 nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
The young's double slit experiment is done in a medium of refractive index 4/3.A light of 600nmwavelength is falling on the slits having 0.45 mm separation .The lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index1.5.the intereference pattern is observed ona screen placed 1.5m from the slits are shown
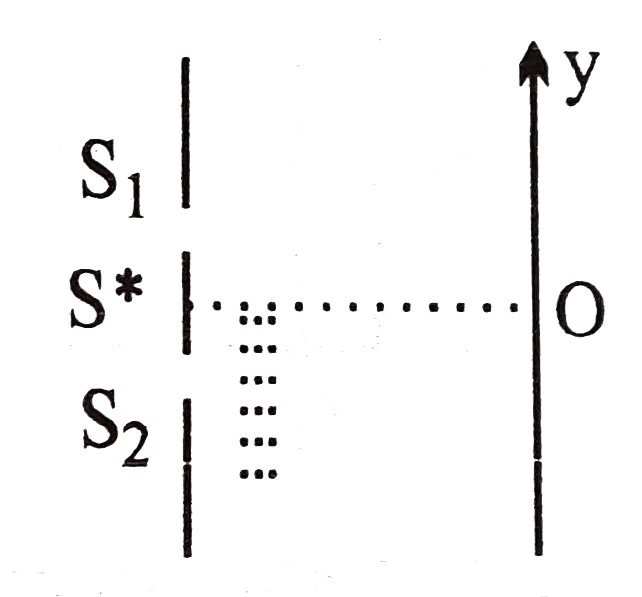
(a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis.
(b) Find the light intensity at point Orelative to the maximum fringe intensity.
(c )Now,if 600nmlight is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O.[All wavelengths in this problem are for the given medium of refractive index 4/3 .Ignore dispersion]
View SolutionYoung’s double slit experiment is done in a medium of refractive index 4/3. Light of 600 nm wavelength is falling on the slits having 0.45 pm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 pm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown.
(a) Find the location of central maxima (bright fringe with zero I t y path difference) on the y-axis.
(b) Find the light intensity at point O relative to the maximum fringe intensity.
(c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that from maxima exactly at point O[All wavelengths in this problem are for the given medium of refractive index 43. Ignore dispersions.]
View Solution
Knowledge Check
A YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
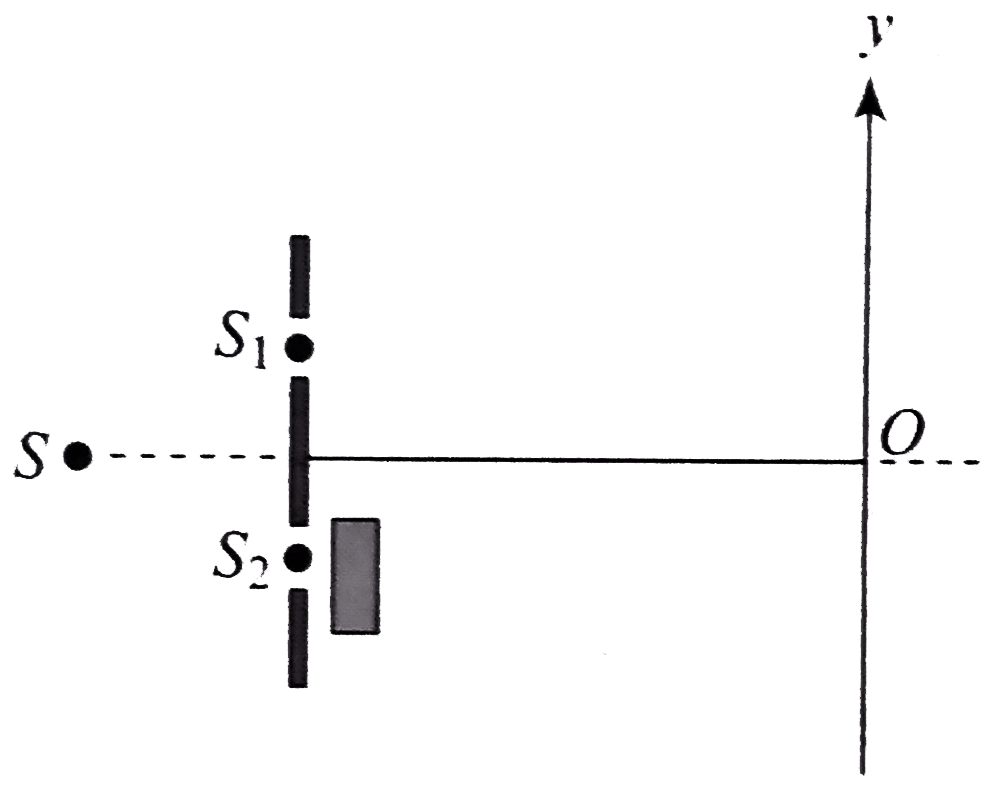
Find the light intensity at point O relative t maximum fringe intensity.A14ImaxB54ImaxC12ImaxD34ImaxA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
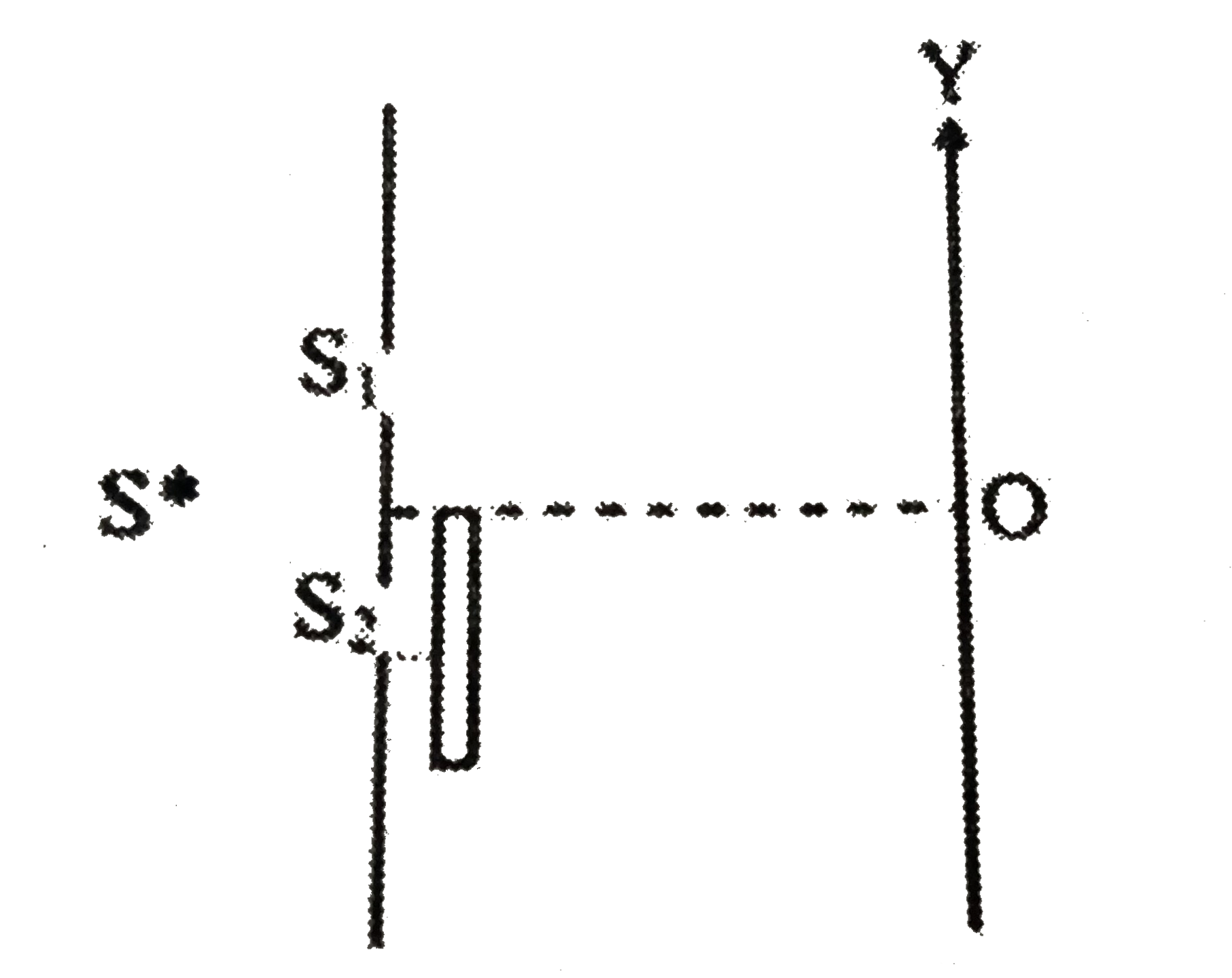
Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.A650 nm, 433.3 nmB550 nm, 750 nmC450 nm, 645.3 nmD375 nm, 525.3 nmThe young's slit experiment is done in a medium of refractive index 4/3 .A light of 600 nm wavelength is falling on the slits having 0.45 mm separation . The lower slit S2 is covered by a thin galss sheet of thickness 10.4 μm and r3efractive index 1.5 .The interferecnce pattern is observed on a screen placed 1.5 m form the slits as shown in figure .Find the light intensity at point O relative to the maximum fringle intensity
(Given:cos3.4=√0.75
 A14B12C34D0
A14B12C34D0
Two slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm
View SolutionTwo slits in YDSE are placed 2 millimeter from each other. Interference pattern is observed on a screen placed 2m from the plane of slits. What is the fringe width for a light of wavelength 400 nm ?
View SolutionTwo slits in YDSE are placed 2 millimetre from each other. Interference pattern is observedon a screen placed 2 m from the plane of slits. What is the fringe width for a light of wavelength 400 nm?
View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:

View SolutionA double slit experiment is performed with light of wavelength 500nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will
View Solution
