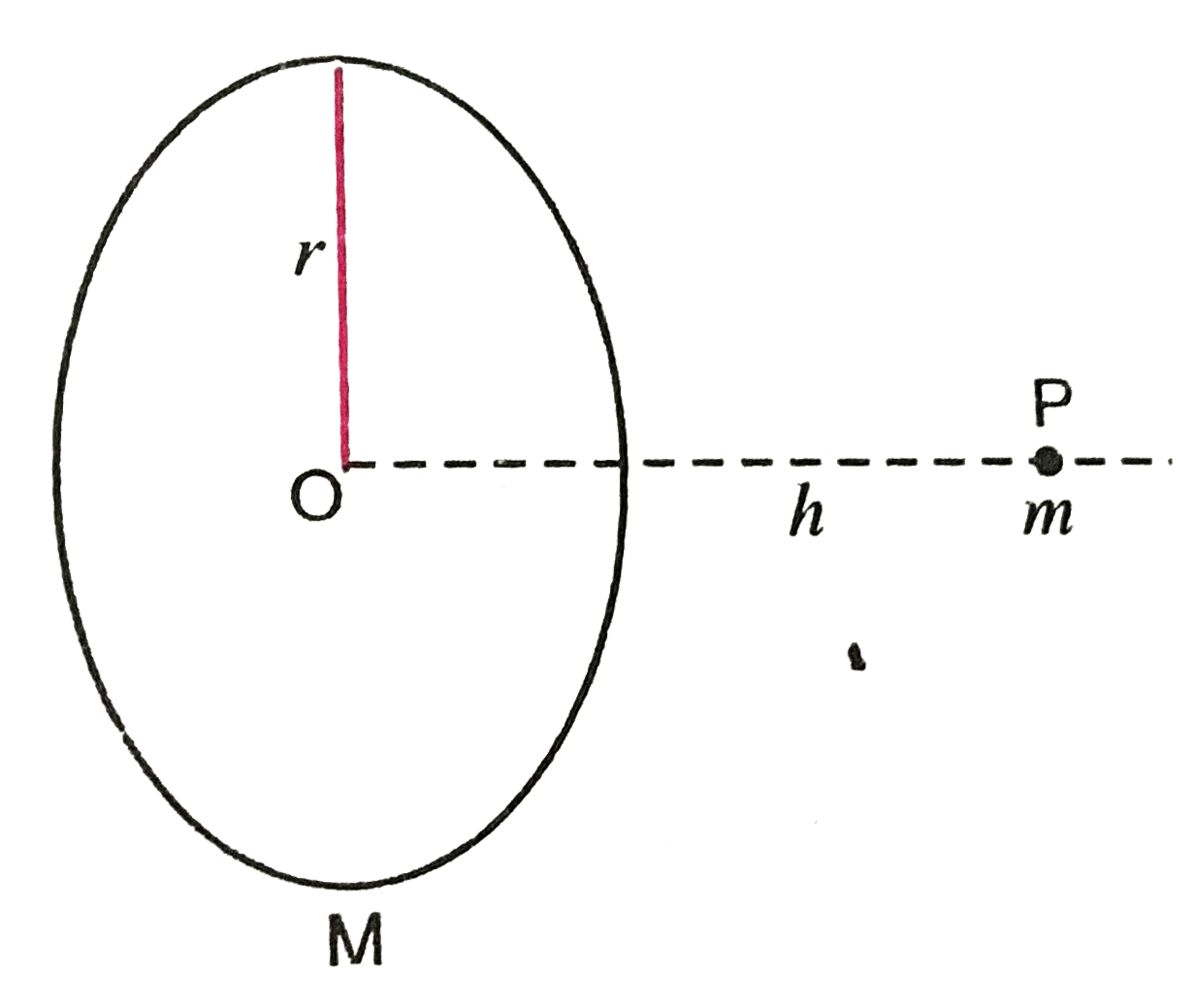
A mass m is placed at P a distance h along the normal through the centre o of a thin circular ring of mass M and radius r (figure).

If the mass is moved further away such that OP becomes 2h by what factor the force of gravitation will decrease, if h = r?Solution in Gujrati
⇒ Gravitational force acting on an object of mass m, placed at point P at a distance h along the normal through the centre of a circular ring of mass M and radius r is given by
F=GMmh(r2+h2)3/2 (along →PO....(i) )
When mass is displaced upto distance 2h, then
F.=GMm×2h[r2+(2h)2]3/2 [∴h.=2h]
=2GMmh(42+4h2)3/2 ....(ii)
when h = r, in eq. (ii) ,
F=GMm×r(r2+r2)3/2⇒F=GMm2√2r2
and F.=2GMmr(r2+4r2)3/2=2GMm5√5r2
∴F.F=4√25√5
⇒F.=4√25√5F
Topper's Solved these Questions
- GRAVITATIONBook:KUMAR PRAKASHANChapter:GRAVITATIONExercise:Section - D NCERT Exemplar Solutions (Long Answer Type Question )
Explore 5 Videos
- GRAVITATIONBook:KUMAR PRAKASHANChapter:GRAVITATIONExercise:Section - E Multiple Choice Questions (MCQs)
Explore 73 Videos
- GRAVITATIONBook:KUMAR PRAKASHANChapter:GRAVITATIONExercise:Section - D NCERT Exemplar Solutions (Very Short Answer Type Question )
Explore 11 Videos
- LAW OF MOTIONBook:KUMAR PRAKASHANChapter:LAW OF MOTIONExercise:(QUESTION PAPER) SECTION-D
Explore 1 Video
Similar Questions
A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Letr be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity , ω kinetic energy K, gravitational potential energy U, total energy E and angular momentum I. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease. As shown in figure, where a body of mass m is revolving around a star of mass M. Linear velocity of the body,
View SolutionWhich one of the following is the physical quantity of the unit Nm2(kg)2 ?
View SolutionMolecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r Fig. If the mass is removed futher away such that OP becomes 2h , by what factor the force of gravitational will decrease, if h = r ?
View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
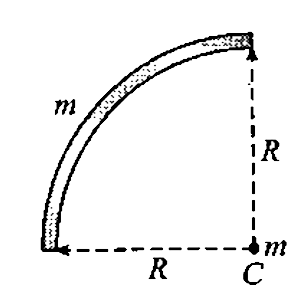
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
View SolutionA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
View SolutionFigure shows a composite body made up by welding a thin rod (of mass m and length r) normally at the centre P of a thin semicircular disc (of mass m and radius r). What are corrdinates of centre of mass of the system ?
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionA point particle of mass m is released from a distance sqrt(3)R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionMoment of inertia of a circular ring of mass m and radius r about the normal axis passing through its centre is
View Solutionएक M द्रव्यमान एवं R त्रिज्या वाले किसी वलय के अक्ष पर स्थित P बिन्दु पर इसके केंद्र से R दूरी पर m द्रव्यमान को आरोपित किया जाता है। m द्रव्यमान पर गुरुत्वीय बल है-
View SolutionA mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r Fig.
If the mass is removed futher away such that OP becomes 2h, by what factor the force of gravitational will decrease, if h=r ?
View Solution

