Na22 has half life of 2.68 years . It decays both by positron emission and electron capture with a ratio of 86% of the former to 14% of the later . The half life for positron emission in years (nearly) is ……….Solution in Telugu
The correct Answer is:3

t1/2=0.693λ1=0.6930.2224=3.116≡3,YA=λ1λ×100=86lλ=0.6932.68……….(2)
YB=λ2λ×100=14,λ=(λ1+λ2)……...(3)⇒λ1λ2=8614......(1) From (1) , (2) and (3)
λ=(λ1+λ2)=0.6932.68,(λ1+14λ180)=0.2586,λ1(1+1480)=0.2586
λ1=0.2586×86100=0.2244,t1/2=0.693λ1=0.6930.2224=3.116≡3
Topper's Solved these Questions
- NUCLEAR CHEMISTRY Book:AAKASH SERIESChapter:NUCLEAR CHEMISTRY Exercise:PRACTICE SHEET - 1 (Single or more than one option questions)
Explore 15 Videos
- NUCLEAR CHEMISTRY Book:AAKASH SERIESChapter:NUCLEAR CHEMISTRY Exercise:PRACTICE SHEET - 1 (Linked Comprehension type questions )
Explore 6 Videos
- NUCLEAR CHEMISTRY Book:AAKASH SERIESChapter:NUCLEAR CHEMISTRY Exercise:LECTURE SHEET (LEVEL- II) (EXERCISE - III) (Match the following questions )
Explore 3 Videos
- NOBLE GASESBook:AAKASH SERIESChapter:NOBLE GASESExercise:PRACTICE SHEET - 2 (Single more than one option questions)
Explore 5 Videos
- PERIODIC TABLEBook:AAKASH SERIESChapter:PERIODIC TABLEExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 37 Videos
Similar Questions
The triad of nuclei that represents isotopes is :
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure . The rate of radioactive disintegration (Activity) is represented as −dNdt=λN , Where λ = decay constant , N number of nuclei at time t , N0 = initial no. of nuclei.
The above equation after integration can be represented as λ=2.303tlog(N0N)
Half-life period of U232 is 2.5×105 years . In how much time will the amount of U237 remaining be only 25% of the original amount ?
View SolutionMatch the Column - I Radio-isotope with Column - II medicinal use and select correct matching :
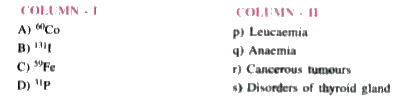
View SolutionWhich compound is prepared by the following reaction :Xe+2F2Ni vessel−−−−−−−−→673K,5−6atm1:5volume ratio
View SolutionWrite on the IUPAC nomenclature of the elements with atomic number greater than 103.
View SolutionCu^(64)(" half life" =12.8 "hours" ) decay by beta^(c-)- emission (38%), beta^(o+)- emission(19%), and electron capture (43%) . Write the decay products and calculate partial half lives for each of the decay processes.
View SolutionA ratio isotope has a half-life of 75 years. The fraction the atoms of this material that would decay in 150 years. Will be.
View SolutionDecrease in atomic number is observed during A) alpha -emission B) beta -emission C) Positron emission D) electron capture
View Solution^64Cu (half - life = 12.8 h) decays by beta emission (38%) , beta^(+) emission (19%) and electron capture (43%) Write the decay products and calculate partial half - lives for each of the decay processes.
View SolutionNa""^(22) has half life of 2.68 years. It decays both by positron emission and electron capture with a ratio of 86% of the former to 14% of the later. The half life for positron emission in years (nearly) is
View SolutionOne gm of an element decays by beta -emission to 0.125 gm in 200 years . The half life period of the reaction is
View SolutionNuclei of .64Cu can decay be electron capture (probability 61%) or by β+ decay (39%). Half life of .64Cu is 12.7 hour. Find the partial half life for electron capture decay process,
View SolutionThe half-life for decay of .14C by β−emission is 5730 years. The fraction of .14C decays, in a sample that is 22,920 years old, would be
View SolutionA radioactive material has a half life of 600 years and 300 years for alpha and beta emissions respectively. The material decays by simultaneous alpha and beta emissions respectively . The material decays by simultaneously alpha and beta emissions . What is time in which 3/4 th of the material will decay ?
View SolutionRadioactive nucleus A decays into B with half-life 10sec. A also convert into C with half-life 100sec. Find half-life of A for both emission.
View Solution

