Upon irradiating californium with neutrons , a scientist discovered a new nuclide having mass number of 250 and a half-life of 30 min . 90 min after the irradiation, the observed radioactivity due to nuclide was 100 dis/min . If 3.46×10x atoms of the nucleide were present initially . Then x is ..........Solution in Telugu
The correct Answer is:4
A030min−−→A0230min−−→A0430min−−→A08=100⇒A0=800 dpm
A=λN,800=0.69330×Nt , where Nt=800×300.693=3.46×104 atoms
Topper's Solved these Questions
- NUCLEAR CHEMISTRY Book:AAKASH SERIESChapter:NUCLEAR CHEMISTRY Exercise:PRACTICE SHEET - 1 (Single or more than one option questions)
Explore 15 Videos
- NUCLEAR CHEMISTRY Book:AAKASH SERIESChapter:NUCLEAR CHEMISTRY Exercise:PRACTICE SHEET - 1 (Linked Comprehension type questions )
Explore 6 Videos
- NUCLEAR CHEMISTRY Book:AAKASH SERIESChapter:NUCLEAR CHEMISTRY Exercise:LECTURE SHEET (LEVEL- II) (EXERCISE - III) (Match the following questions )
Explore 3 Videos
- NOBLE GASESBook:AAKASH SERIESChapter:NOBLE GASESExercise:PRACTICE SHEET - 2 (Single more than one option questions)
Explore 5 Videos
- PERIODIC TABLEBook:AAKASH SERIESChapter:PERIODIC TABLEExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 37 Videos
Similar Questions
The triad of nuclei that represents isotopes is :
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure . The rate of radioactive disintegration (Activity) is represented as −dNdt=λN , Where λ = decay constant , N number of nuclei at time t , N0 = initial no. of nuclei.
The above equation after integration can be represented as λ=2.303tlog(N0N)
Half-life period of U232 is 2.5×105 years . In how much time will the amount of U237 remaining be only 25% of the original amount ?
View SolutionMatch the Column - I Radio-isotope with Column - II medicinal use and select correct matching :
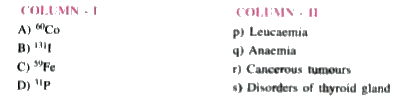
View SolutionWhich compound is prepared by the following reaction :Xe+2F2Ni vessel−−−−−−−−→673K,5−6atm1:5volume ratio
View SolutionWrite on the IUPAC nomenclature of the elements with atomic number greater than 103.
View SolutionA certain nuclide has a half life period of 30 min. If a sample containing 600 atoms is allowed to decay for 90 min, how many atoms will remains?
View SolutionUpon irradiating californium with neutrons, a scientist discovered a new nuclide having mass scientist discovered a new nuclide having mass number of 250 and a half-life of 0.50hr. Three hours after the irradiation the observated radioactivity due to the nuclide was 10dis/min. How many atoms of the nuclide were perepared initially?
View SolutionTwo radioactive nuclides A and B have half-lives 50 min and 10 min respectively . A fresh sample contains the nuclides of B to be eight times that of A. How much time should elapse so that the mumber of nuclides of A becomes double of B ?
View SolutionUpon irradiating californium with neutrons, a scientist discovered a new nuclide having mass number of 250 and a half-life of 30 min. After 90 min. of irradiation, the observed radioactivity due to nuclied was 100 dis/min. How many atoms of the nucliede were prepared intially?
View SolutionMean life of a radioactive sample is 100s . Then ,its half-life (in min) is
View SolutionHalf life of a radioactive substance is 60 min. After 3 hours, the fraction of total number of atoms that have decayed would be
View SolutionThe activity of a radioactive nuclide is 2×107 disintegrations per minute (dpm). After 23.03 minutes, its activity is reduced to 2×106 dpm. What is the average life (in min) of this nuclide
View SolutionThe half life of 2g sample of radioactive nuclide 'X' is 15 min. The half life time of 1g sample of X is
View SolutionThe half period of a radioactive element is 20 years. If a sample of this nucleide has an initial activity of 20000 dis/min, the activity after 80 years would be:
View SolutionA certain nucleide has half life period of 30 min. If a sample containing 6xx10^(10) atoms is allowed to decay for 90 min, how many atoms will remain ?
View Solution

