Potential inside a uniformly charged solid sphere is given by Qa+b(rR)c4πε0 What are the values of a,b,c?
a=32,b=−12,c=2
a=12,b=−12,c=2
a=32,b=12,c=2
a=32,b=−12,c=−2
To find the values of a, b, and c in the expression for the electric potential inside a uniformly charged solid sphere, we start with the known formula for the potential inside such a sphere.
1. Understand the Formula for Electric Potential Inside a Solid Sphere:
The electric potential V at a distance r from the center of a uniformly charged solid sphere with total charge Q and radius R is given by:
V(r)=Q4πϵ0(3R2−r22R3)
2. Rearranging the Formula:
We can rearrange the formula to match the form given in the question:
V(r)=Q4πϵ0(32−r22R2)
This can be expressed as:
V(r)=Q4πϵ0(32−12(rR)2)
3. Identifying Constants:
Now, we can identify the constants a, b, and c from the expression:
- The constant term a corresponds to 32.
- The coefficient of (rR)2 gives us b=−12.
- The power of (rR) is c=2.
4. Final Values:
Thus, we find:
- a=32
- b=−12
- c=2
Conclusion:
The values of a, b, and c are:
- a=32
- b=−12
- c=2
The electric potential V at a distance r from the center of a uniformly charged solid sphere with total charge Q and radius R is given by:
V(r)=Q4πϵ0(3R2−r22R3)
We can rearrange the formula to match the form given in the question:
V(r)=Q4πϵ0(32−r22R2)
This can be expressed as:
V(r)=Q4πϵ0(32−12(rR)2)
Now, we can identify the constants a, b, and c from the expression:
- The constant term a corresponds to 32.
- The coefficient of (rR)2 gives us b=−12.
- The power of (rR) is c=2.
Thus, we find:
- a=32
- b=−12
- c=2
The values of a, b, and c are:
- a=32
- b=−12
- c=2
Topper's Solved these Questions
Similar Questions
There are two spheres of radii R and 2R having charges Q and Q2 respectively. These two spheres are connected with a cell of emf V volts as shown in figure. When switch is closed, the final charge on sphere of radius 2R is Q+8πε0RVn . Then find the value of n.
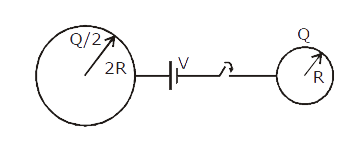
View SolutionIf the potential at the center of a uniformly charged sphere of radius R is V then electric field at a distance r from the center of sphere will be (r<R) : -
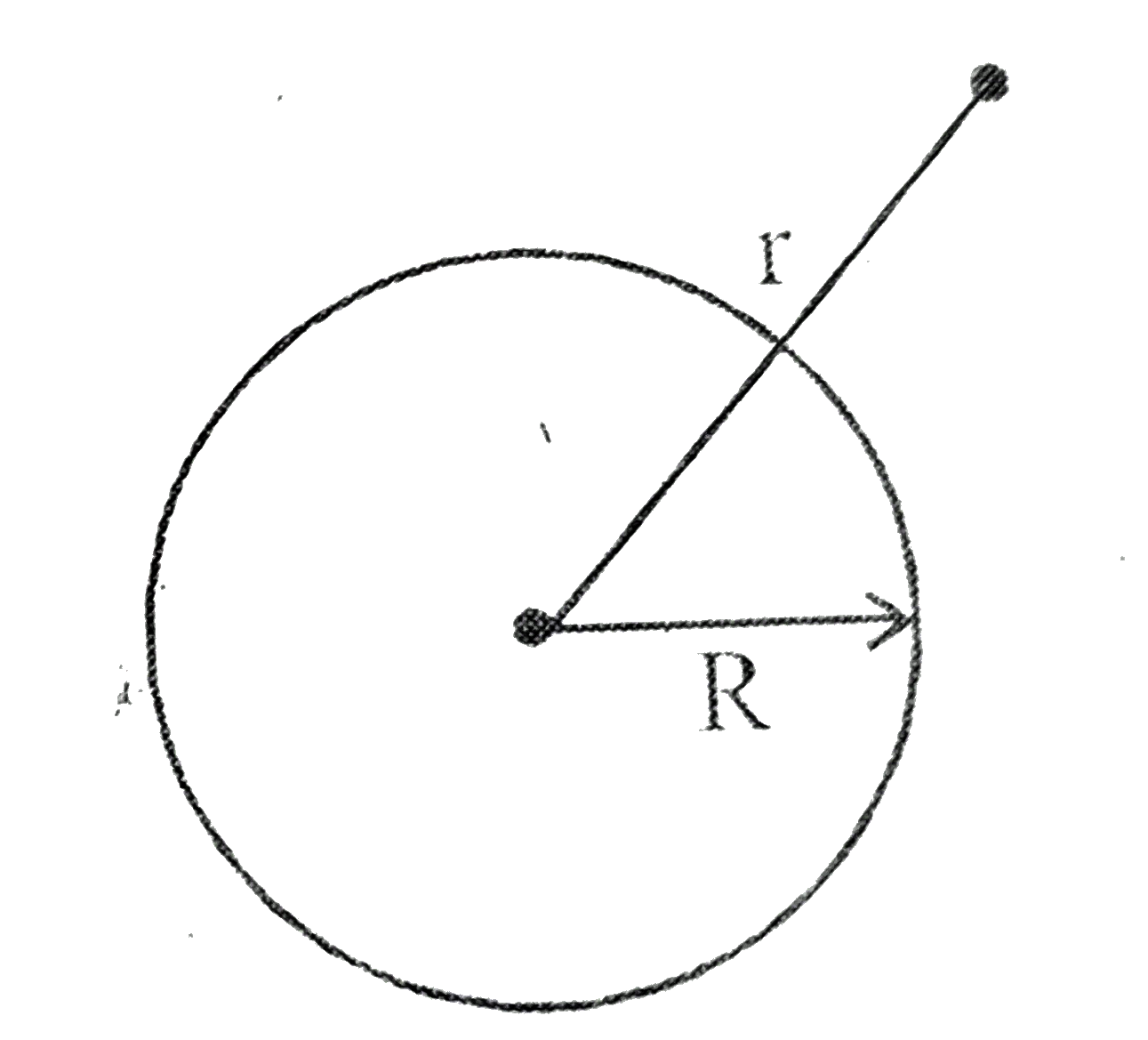
View Solution
Knowledge Check
Consider a sphere of radius R with unform charged density and total charge Q. The electrostatic potential distribution inside the sphere is given by ϕ(r)=Q4πε0R(a+b(r/R)c) Note that the zero of potential is at infinity. The values of (a, b, c) are :-
A(12,−32,1)B(32,−12,2)C(12,12,1)D(12,−12,2)Flux (ph) as a function of distance (r) from centre of uniformly charged solid sphere of charge Q and radius R, is best represented by
A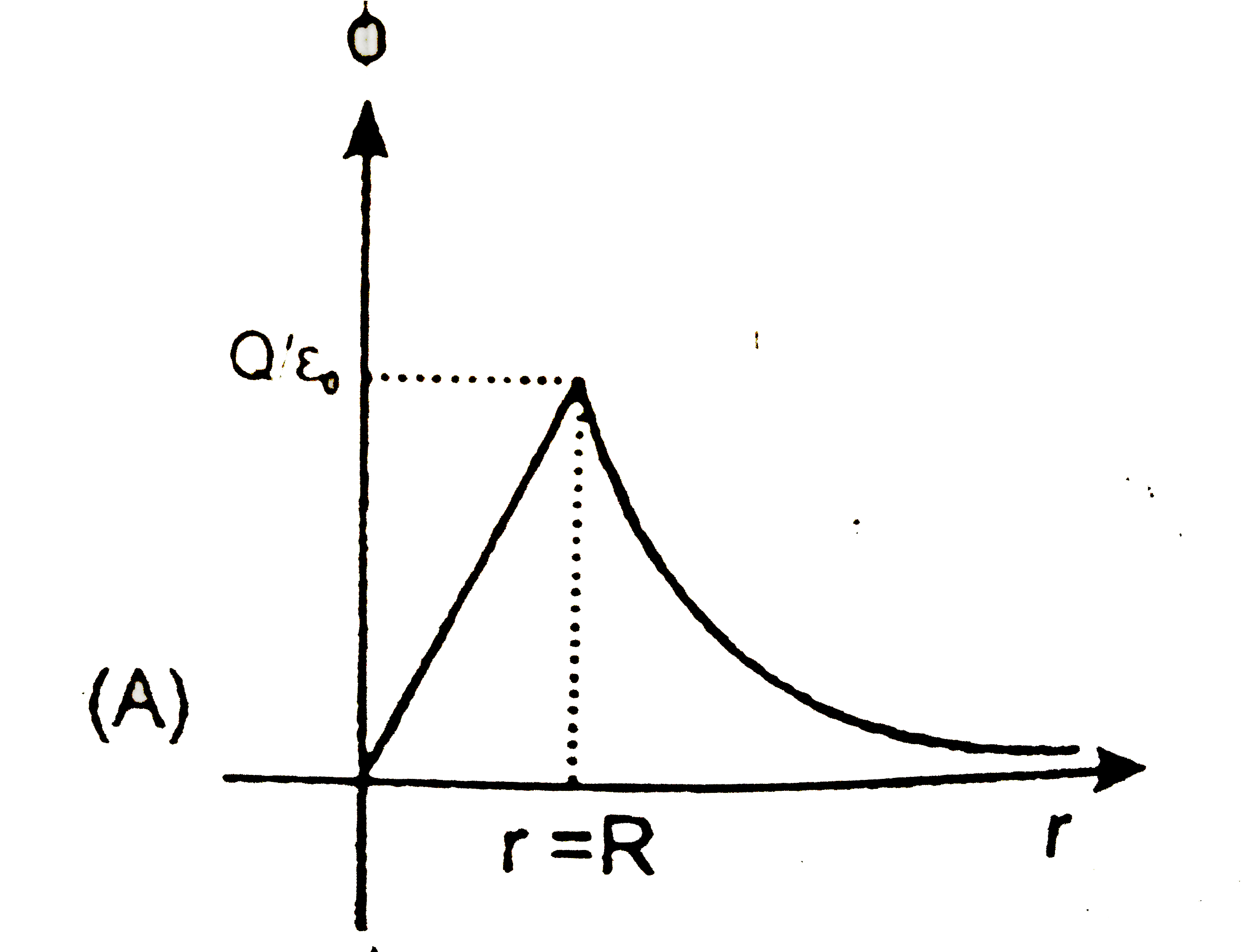 B
B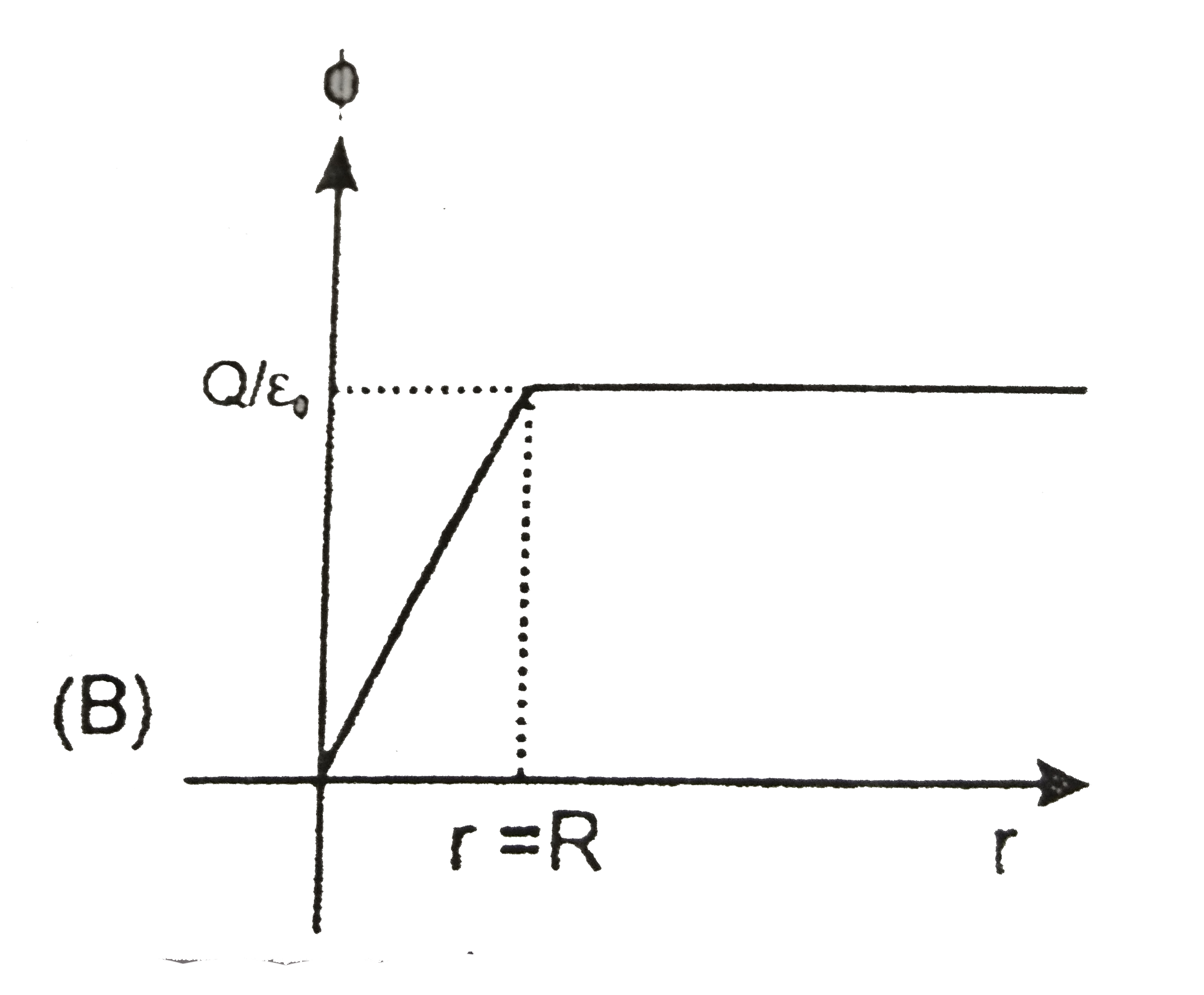 C
C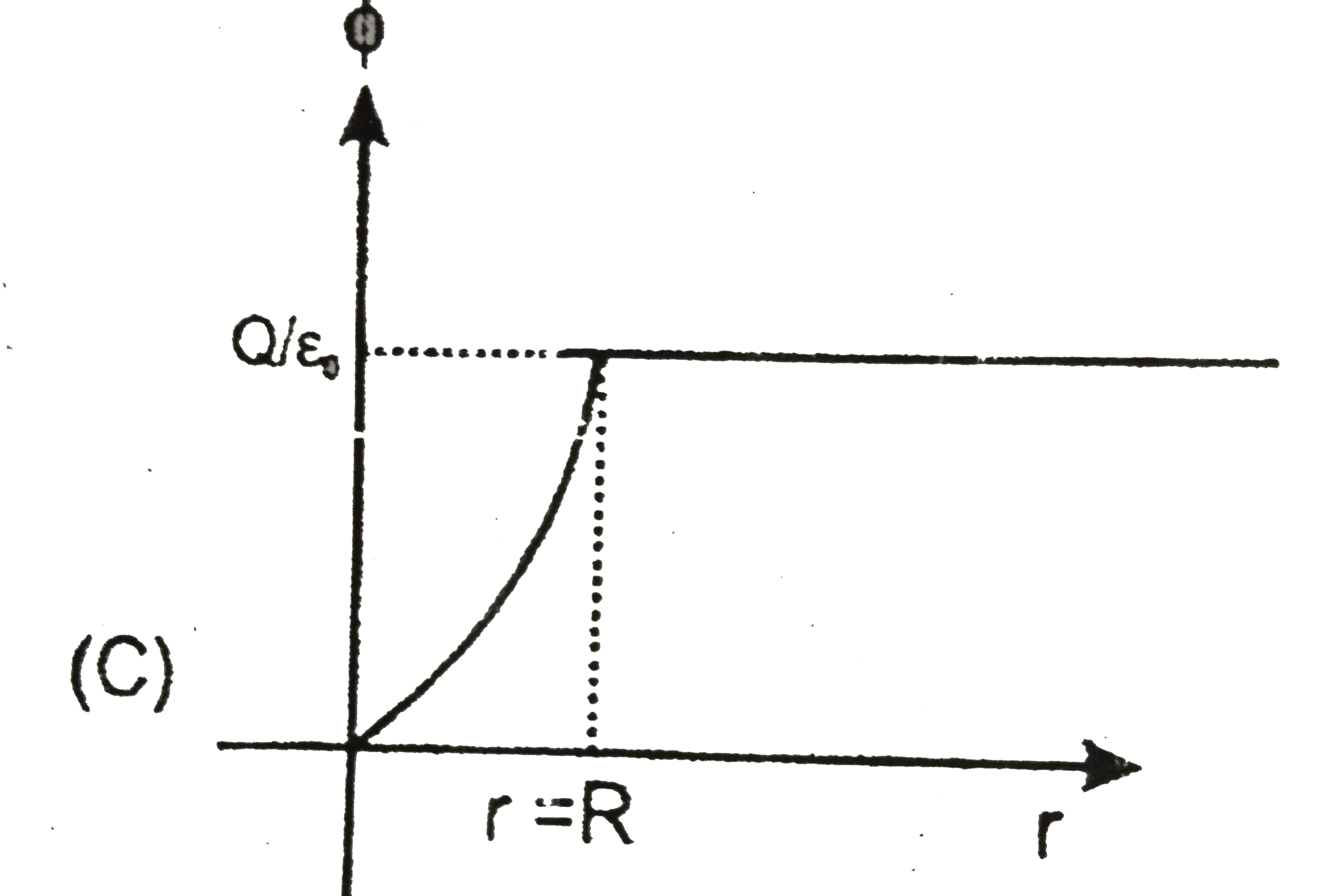 D
D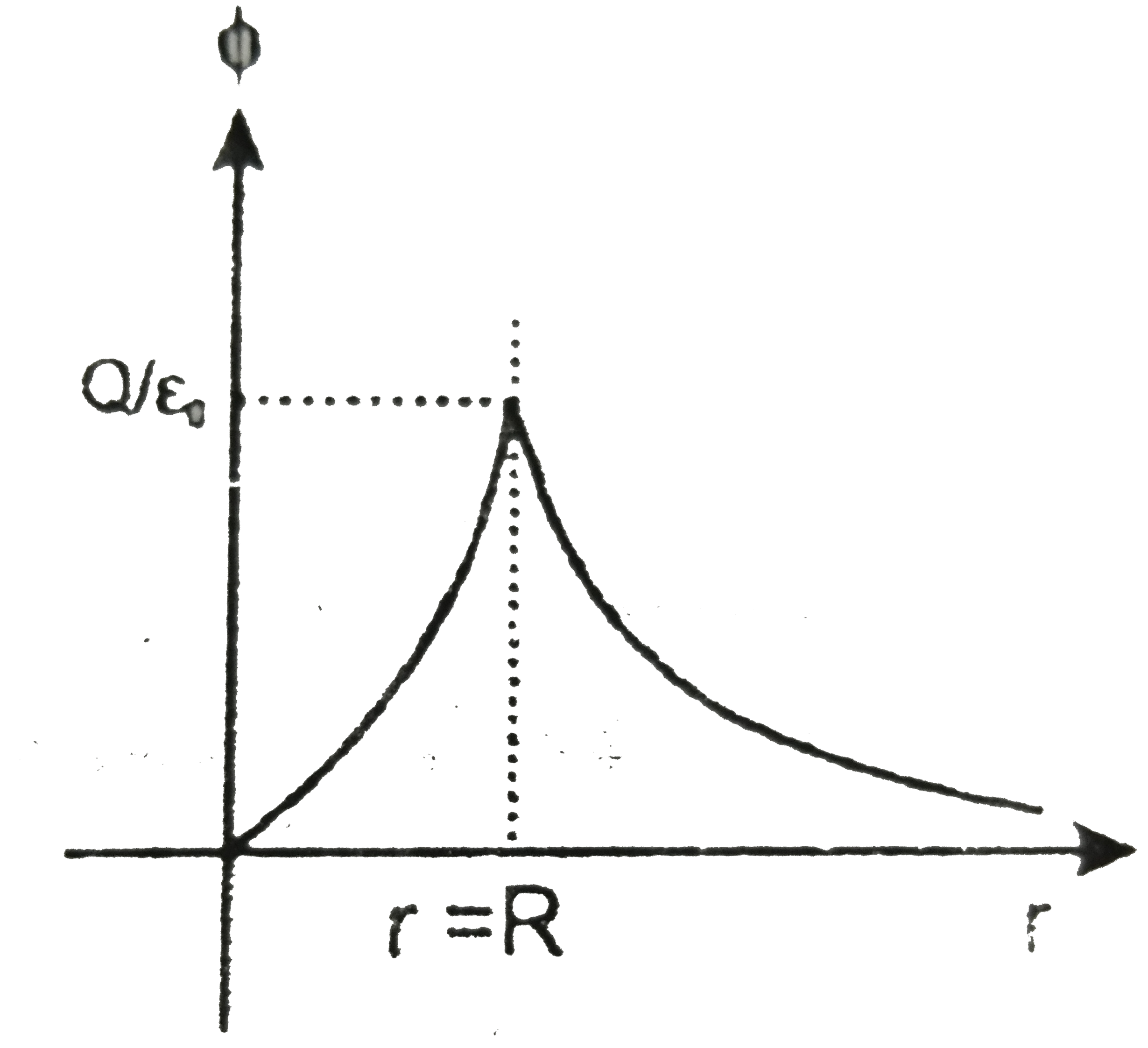
A conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common center of AandB. Study the following statements.
(i) The potential at a distance r from C, where
a≤r≤b,is14πε0(qr)
(ii) The potential difference between AandB is
14πε0Q(1r−1B)
(iii) The potential at a distance r from C, where
a≤r≤b,is14πε0Q(1r−1B)
Which of the above statements are correct ?
 .AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these
.AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these
Consider a system of three charges q3,q3and−2q3 placed ar point A,B and C respectively, as shown in the figure. Take O to be the centre of the circle of radius R and angle CAB=60∘. Choose the incorrect options
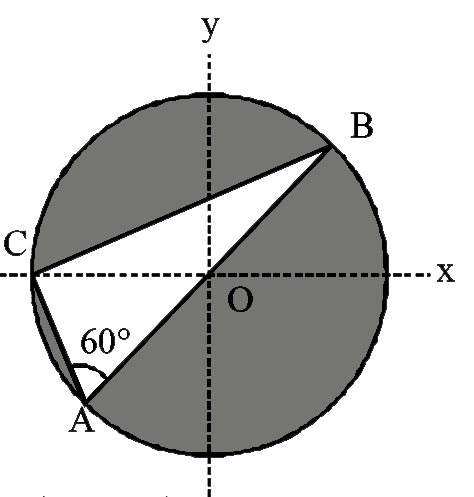
(1) The electric field at point O is q8πε0R2 directed along the negative x-axis
(2) The potential energy of the system is zero
(3) The potential at point O is q12πε0R
(4) The magnitude of the force between the charges at C and B is q254πε0R2
View SolutionThe volume charge density inside of sphere of radius R is given by ρ=ρ0(1−rR) ,where ρ0 is constant and r distance from centre.
(a) Find total charge Q inside sphere.
Electric field outside sphere at distance r from centre.
(b) Electric field outside sphere at distance r from centre.
(c) Electric field inside sphere at distance r from centre.
(d) At what distance from centre electric field is maximum and its value?
(e ) Sketch E versus r graph.
View SolutionFor spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View SolutionThe given graph shows variation (with distance r from centre) of (A)Electric field of a uniformly charged conducting sphere (B)Electric field of a uniformly charged non-conducting sphere (C) Potential of a uniformly charged hollow sphere (D)Potential of a uniformly charged non- conducting solid sphere
View SolutionA solid sphere ofradius 'R' is uniformly charged with charge density ρin its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. It is given that ρR2∈0=48V. Find the electric potential at the centre C of the sphere:

View Solution