What is the greatest value of θ lying between 0∘ and 720∘ whose tangent is −1√3 ?
The correct Answer is:690∘
To find the greatest value of θ lying between 0∘ and 720∘ for which tanθ=−1√3, we can follow these steps:
Step 1: Identify the reference angle
The value −1√3 corresponds to angles where the tangent function is negative. The reference angle for tanθ=1√3 is 30∘ or π6.
Step 2: Determine the quadrants
Since tangent is negative in the second and fourth quadrants, we can find the angles:
- In the second quadrant:
θ=180∘−30∘=150∘
- In the fourth quadrant:
θ=360∘−30∘=330∘
Step 3: Find the general solutions
The general solutions for tanθ=−1√3 can be expressed as:
θ=150∘+n⋅180∘andθ=330∘+n⋅180∘
where n is any integer.
Step 4: Calculate specific values of θ
Now, we will calculate the values of θ for n=0,1,2,… until we exceed 720∘.
1. For n=0:
- From 150∘: θ=150∘
- From 330∘: θ=330∘
2. For n=1:
- From 150∘: θ=150∘+180∘=330∘
- From 330∘: θ=330∘+180∘=510∘
3. For n=2:
- From 150∘: θ=150∘+2⋅180∘=510∘
- From 330∘: θ=330∘+2⋅180∘=690∘
4. For n=3:
- From 150∘: θ=150∘+3⋅180∘=690∘
- From 330∘: θ=330∘+3⋅180∘=870∘ (exceeds 720∘)
Step 5: Identify the greatest value
The values we have calculated that are within the range 0∘ to 720∘ are:
- 150∘
- 330∘
- 510∘
- 690∘
The greatest value of θ is:
θ=690∘
Final Answer
Thus, the greatest value of θ lying between 0∘ and 720∘ for which tanθ=−1√3 is:
690∘
The value −1√3 corresponds to angles where the tangent function is negative. The reference angle for tanθ=1√3 is 30∘ or π6.
Since tangent is negative in the second and fourth quadrants, we can find the angles:
- In the second quadrant:
θ=180∘−30∘=150∘
- In the fourth quadrant:
θ=360∘−30∘=330∘
The general solutions for tanθ=−1√3 can be expressed as:
θ=150∘+n⋅180∘andθ=330∘+n⋅180∘
where n is any integer.
Now, we will calculate the values of θ for n=0,1,2,… until we exceed 720∘.
- From 150∘: θ=150∘
- From 330∘: θ=330∘
- From 150∘: θ=150∘+180∘=330∘
- From 330∘: θ=330∘+180∘=510∘
- From 150∘: θ=150∘+2⋅180∘=510∘
- From 330∘: θ=330∘+2⋅180∘=690∘
- From 150∘: θ=150∘+3⋅180∘=690∘
- From 330∘: θ=330∘+3⋅180∘=870∘ (exceeds 720∘)
The values we have calculated that are within the range 0∘ to 720∘ are:
- 150∘
- 330∘
- 510∘
- 690∘
θ=690∘
Thus, the greatest value of θ lying between 0∘ and 720∘ for which tanθ=−1√3 is:
690∘
Topper's Solved these Questions
- TRIGONOMETRYBOOK - MCGROW HILL PUBLICATIONCHAPTER - TRIGONOMETRYEXERCISE - Multiple Choice Questions
50 Videos
- TRANSPARENT PAPER FOLDING BOOK - MCGROW HILL PUBLICATIONCHAPTER - TRANSPARENT PAPER FOLDING EXERCISE - EXAMPLE
2 Videos
- VERIFICATION OF TRUTH OF THE STATEMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - VERIFICATION OF TRUTH OF THE STATEMENTEXERCISE - Exercise
25 Videos
Similar Questions
Knowledge Check
The value of θ lying between 0 and π2 and satisfying the equation
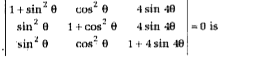 A7π24or11π24B5π24C3π24Dnone of these
A7π24or11π24B5π24C3π24Dnone of theseIf cos40∘=xandcosθ=1−2x2, then the possible values of θ lying between 0∘ and 360∘ is
A100∘and260∘B80∘and280∘C280∘and110∘D110∘and260∘The greatest integer lying between -10 and -15 is
A−10B−11C−15D−14
Solve tanθ+secθ=√3 for the values of θ between 0 and 2π
View SolutionThe greatest value of cosθ for which cos5θ=0 is
View SolutionThe value of θ lying between θ=0andθ=π2 and satisfying the equation
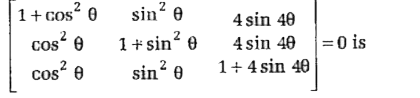
View SolutionThe values of θ in between 0∘ and 360∘ and satisfying the equation tanθ+1√3=0 is equal to
View SolutionWhat is the value of 20% of 2/3 of 720?
View Solution
