The values of θ in between 0∘ and 360∘ and satisfying the equation tanθ+1√3=0 is equal to
θ=150∘and300∘
θ=120∘and300∘
θ=60∘and240∘
θ=150∘and330∘
The correct Answer is:D
Step by step video, text & image solution for The values of theta in between 0^(@) and 360^(@) and satisfying the equation tantheta+(1)/(sqrt(3))=0 is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Competitive Thinking
218 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Evaluation Test
34 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Evaluation Test
34 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - TARGET PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Evaluation Test
9 Videos
- VECTORSBOOK - TARGET PUBLICATIONCHAPTER - VECTORSEXERCISE - Evaluation Test
18 Videos
Similar Questions
Knowledge Check
The value of θ lying between 0 and π2 and satisfying the equation
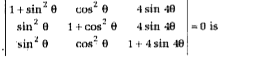 A7π24or11π24B5π24C3π24Dnone of these
A7π24or11π24B5π24C3π24Dnone of theseThe value of θ lying between θ=0andθ=π2 and satisfying the equation
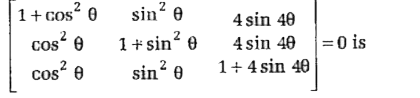 A11π24B7π24C5π24Dπ24
A11π24B7π24C5π24Dπ24If sinθ=−12 and tanθ=1√3 then θ is equal to,
A30∘B150∘C210∘Dnone of these
There exists a value of θ between 0 and 2π that satisfies the equation sin4θ−2sin2θ−1=0
View SolutionThe set of angles between 0 and 2π satisfying the equation 4cos2θ−2√2cosθ−1=0 is
View SolutionThe set of angles between 0 and 2π satisfying the equation 4cos2θ−2√2cosθ−1=0 is
View SolutionThere exist a value of θ between 0 and 2π that satisfies the equaition sin4θ−2sin2θ+1=0
View SolutionThe number of values of θ between −πand3π2 that satisfies the equation 5cos2θ+2cos2θ2+1=0 is :
View Solution
